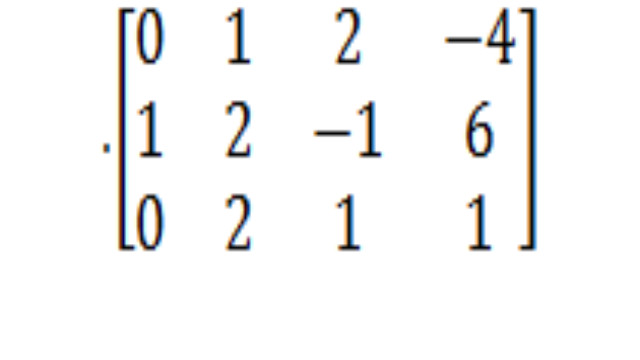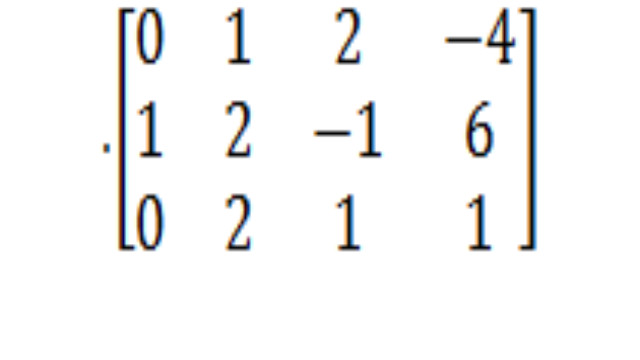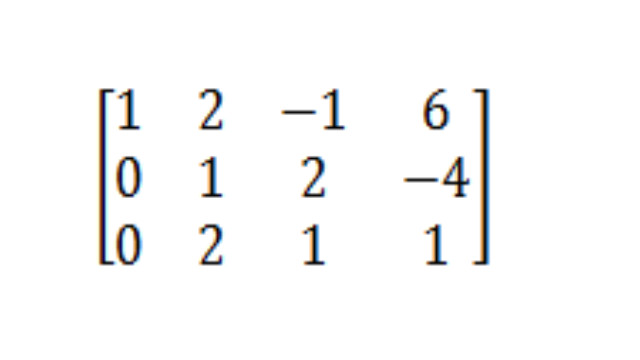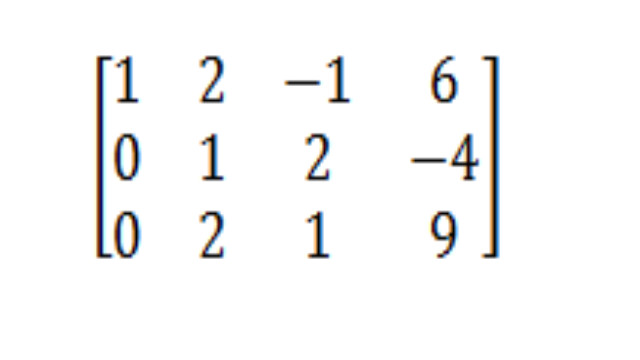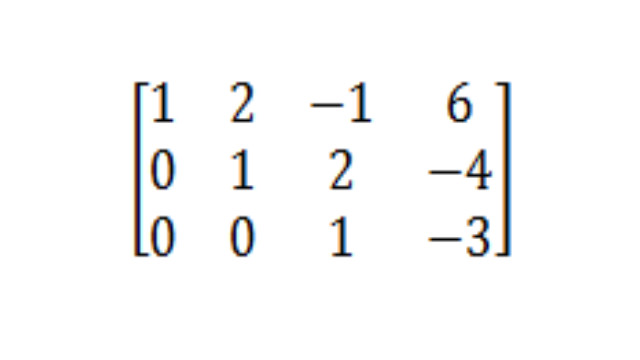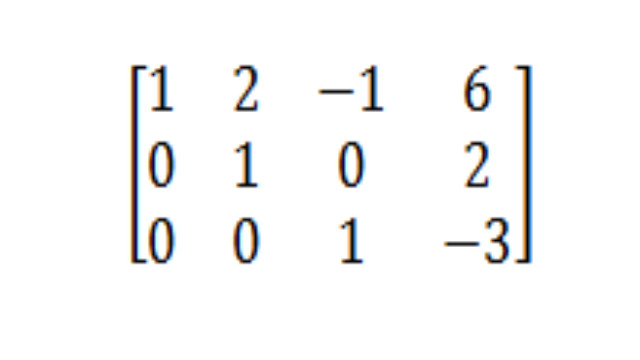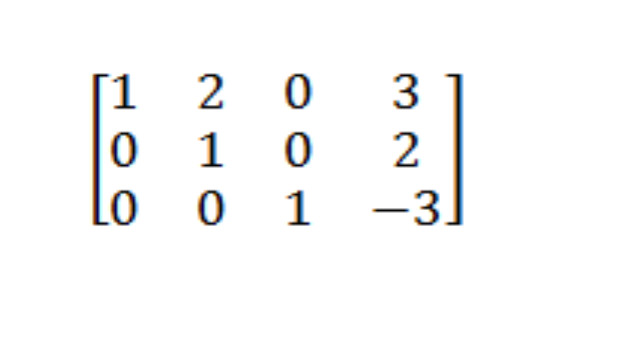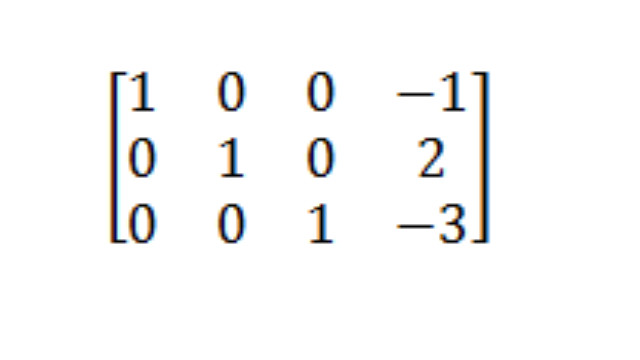The Game of Gaussian Elimination: An Introduction to Linear Algebra
गाऊसी उन्मूलन का खेल:रैखिक बीजगणित का एक परिचय (Introduction to The Game of Gaussian Elimination:An Introduction to Linear Algebra):
- गाऊसी उन्मूलन का खेल:रैखिक बीजगणित का एक परिचय (The Game of Gaussian Elimination:An Introduction to Linear Algebra) में आव्यूह का प्रयोग किया गयाहै.गणित की विभिन्न शाखाओं में आव्यूह के ज्ञान की आवश्यकता पड़ती है.आव्यूह,गणित के सर्वाधिक शक्तिशाली साधनों में से एक है.अन्य सीधी-सीधी विधियों की तुलना में यह गणितीय साधन कार्य को काफी हद तक सरल कर देता है.
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
1.गाऊसी उन्मूलन का खेल:रैखिक बीजगणित का एक परिचय (The Game of Gaussian Elimination:An Introduction to Linear Algebra):
- बीजगणित से मातृवंश की भूमि तक छलांग लेना
स्वीकारोक्ति: मुझे रैखिक बीजगणित बहुत पसंद है। ठीक है, हो सकता है कि यह एक स्वीकारोक्ति के अधिक नहीं है, लेकिन मैं इसे प्यार करता हूँ! एक बड़े हिस्से में, क्योंकि रैखिक बीजगणित बाकी गणित की तरह महसूस नहीं करता है, यह एक पहेली की तरह लगता है। - अब वह पागल लग सकता है, लेकिन मेरी बात सुन लो।
- मेट्रिसेस और वैक्टर की यह नई भूमि भयभीत कर सकती है और महसूस कर सकती है, और अच्छे कारण के लिए: नया अंकन, नए नियम, नए गुण। यह थोड़ा अलग है। लेकिन शायद इसे एक पहेली के रूप में देखने से आपको उस नए नोटेशन बाधा पर कूदने में मदद मिलेगी।
- यह एक कोशिश देने के लिए तैयार हैं?
2.कहा से शुरुवात करे? (Where to start?):
- मेरा मानना है कि रेखीय बीजगणित के साथ शुरू करने के लिए सबसे अच्छी जगह समीकरणों को सुलझाने की प्रणाली के साथ है क्योंकि यह कुछ ऐसा है जिसे आप शायद पहले से ही सीख चुके हैं। प्रतिस्थापन और उन्मूलन के तरीकों को याद रखें ?? क्या वो घंटी बजाते हैं? यदि नहीं, तो आप अपनी स्मृति को यहाँ ताज़ा कर सकते हैं।
- आज हम गौसियन उन्मूलन नामक एक विधि का उपयोग करके समीकरणों की प्रणालियों को हल करने के लिए एक नया दृष्टिकोण लेने जा रहे हैं।
Also Read This Article:Why-I love reading about abstract mathematics theory
3.गाऊसी उन्मूलन क्या है ?? (What is Gaussian Elimination??):
- गाऊसी उन्मूलन एक ऐसी विधि है जहां हम अपने समीकरणों का एक मैट्रिक्स में अनुवाद करते हैं और सिस्टम को हल करने के लिए मैट्रिक्स का उपयोग करते हैं (यानी प्रत्येक चर के लिए समाधान खोजें जो सभी समीकरणों को सच बनाते हैं)।
- मैं आज आपको एक सरल उदाहरण के माध्यम से चरण-दर-चरण चलने जा रहा हूं (संख्या अच्छी तरह से काम करती है इसलिए अभी तक बहुत कम कदम हैं!)। यदि आप अधिक गहराई से उदाहरण चाहते हैं, तो नीचे दिए गए l
4.स्थापित करना (The Set Up):
- जैसे फेरबदल और व्यवहार करके कार्ड गेम शुरू करना, गॉसियन एलिमिनेशन के हमारे खेल की शुरुआत एक मैट्रिक्स में हमारे समीकरणों का अनुवाद करके शुरू होती है।
यहाँ हम जिस सिस्टम को हल करने जा रहे हैं, वह है:
y+2Z= -4
x+2y-z=6
2y+z=1 - सबसे पहली बात जो आपको पहचाननी है, वह यह है कि हमारे सिस्टम में बहुत सारी छिपी हुई जानकारी है। लाल में मैं प्लेसहोल्डर शून्य और अन्य में जोड़ूंगा।
0x+1y+2z= -4
1x+2y-1z=6
0x+2y+1z=1 - अगला, हम सभी महत्वपूर्ण सांख्यिक सूचनाओं को बाहर के प्रतीकों से अलग करने जा रहे हैं। अब लाल रंग में हाइलाइट किया गया है, आप उन सभी महत्वपूर्ण सूचनाओं को प्राप्त करेंगे जिनके साथ हम काम करेंगे
0x+1y+2z= -4
1x+2y-1z=6
0x+2y+1z=1 - हमें मैट्रिक्स के रूप में ऊपर के संख्यात्मक मानों को फिर से लिखना होगा। हम अक्षरों, समान संकेतों और अतिरिक्त प्रतीकों (लेकिन माइनस सिंबल नहीं!) को छोड़ देंगे और बस उन सटीक क्रमों और नंबरों को लिखें जो वे ऊपर दिखाई देते हैं।
- ऐसा करने के बाद हम बड़े ब्रैकेट प्रतीकों को एक साथ जोड़ने के लिए जोड़ देंगे। यह हमारा मैट्रिक्स है:
Also Read This Article:Gaussian elimination
5.नियम ✅(The Rules ):
- किसी भी खेल की तरह, कुछ नियम हैं जिनका हमें पालन करना है:
आप किसी भी दो पंक्तियों को स्वैप कर सकते हैं
आप किसी भी पंक्ति को एक मूल्य से गुणा या विभाजित कर सकते हैं
आप किसी भी दो पंक्तियों को एक साथ जोड़ या घटा सकते हैं
* नोट: आप इन नियमों को किसी भी एक चाल में जोड़ सकते हैं। - अगर यह अभी तक समझ में नहीं आता है, तो चिंता न करें। जब आप हमारे उदाहरण के माध्यम से काम करते हैं तो आप देखेंगे कि वे कैसे काम करते हैं।
Also Read This Article:Zero is nothing but number
6.कैसे जीतें ? (How to Win):
- जब आपका मैट्रिक्स ऐसा दिखता है तो आप जीत जाते हैं:
- जहां # चिह्न किसी भी संख्या का प्रतिनिधित्व करते हैं, और बाकी मैट्रिक्स में विकर्ण को छोड़कर प्रत्येक स्थिति में शून्य है। इसे Reduced-Row Echelon Form कहा जाता है।
7.चलो खेलें! (Let’s Play!):
- सेटअप चरण के दौरान आपके द्वारा किए गए मैट्रिक्स से शुरू करें। अब हम इस मैट्रिक्स को फिनिश लाइन के पार पाने के लिए नियमों का उपयोग करने जा रहे हैं!
- मैट्रिक्स शुरू करना
मूव 1: स्वैप रो वन और रो टू
इस मैट्रिक्स को जीतने के रूप में प्राप्त करने के लिए बहुत सारे अलग-अलग तरीके हैं, लेकिन मुझे लगता है कि शुरू करने का सबसे आसान तरीका पहली और दूसरी पंक्ति को स्वैप करना है। इस तरह हम पहली पंक्ति की पहली स्थिति में 1 और दूसरी पंक्ति की पहली स्थिति में एक 0 प्राप्त करते हैं।
- मूव 2: -2 बार रो टू टू रो थ्री जोड़ें
एक चीज जो हमें करने की अनुमति है वह एक चरण में कई नियमों का एक साथ उपयोग करना है। इस चाल में, हम -2 बार पंक्ति दो लेंगे और उन उत्पादों को पंक्ति तीन में जोड़ देंगे। यह पंक्ति को दो अपरिवर्तित छोड़ देगा लेकिन हमें तीसरी पंक्ति दूसरी स्थिति में एक शून्य प्राप्त करने में मदद करेगा।
- मूव 3: रो थ्री को -3 से विभाजित करें
अगला, हम केवल पंक्ति तीन को -3 से विभाजित करेंगे ताकि हम तीसरी पंक्ति के तीसरे स्थान पर 1 प्राप्त कर सकें।
- मूव 4: -2 बार रो थ्री को रो टू में जोड़ें
अब हमारे पास नीचे के बाएं कोने में सभी शून्य हैं, जो 1 के विकर्ण से घिरा हुआ है, हम 1 के ऊपर के पदों में शून्य प्राप्त करने पर काम शुरू करने के लिए तैयार हैं। - लेकिन इससे पहले कि हम ऐसा करते हैं, मैं थोड़ा साइड नोट करना चाहता हूं: हमारा मैट्रिक्स वर्तमान में पंक्ति में है। इस रूप में, आप अपनी मैट्रिक्स को समीकरणों के एक सेट में अनुवाद कर सकते हैं, यदि आप चाहें, और आसानी से x, y और z के लिए हल कर पाएंगे। आज हम अपने समीकरण को कम रो इकोलोन फॉर्म में लाने पर काम कर रहे हैं, जिसका अर्थ है कि हम 1 के ऊपर के पदों में शून्य प्राप्त करना चाहते हैं। रैखिक बीजगणित में अक्सर आपको कम से कम पंक्ति वाले इकोलोन रूप में काम करने के लिए कहा जाएगा क्योंकि यह उत्तर को पढ़ने के लिए सबसे आसान रूप है।
- ठीक है, हमारे गणित पर वापस। इस अगले कदम में, हम तीसरी पंक्ति से -2 गुना लेंगे और इसे दूसरी पंक्ति में जोड़ देंगे ताकि हम पंक्ति 2 की तीसरी स्थिति में 0 प्राप्त कर सकें।
- चाल 5: पंक्ति तीन को पंक्ति एक में जोड़ें
इसके बाद, हम बस पंक्ति तीन को पंक्ति -1 से जोड़ेंगे -1 + 1 = 0, इससे हमें पहली पंक्ति की तीसरी स्थिति में 0 प्राप्त करने में मदद मिलेगी।
- मूव 6: -2 बार पंक्ति दो को पंक्ति एक में जोड़ें
अंत में, हम पहली पंक्ति की दूसरी स्थिति में शून्य प्राप्त करने के लिए पहली पंक्ति में -2 बार पंक्ति दो जोड़ देंगे।
- बधाई हो, आप जीत गए !! WIN
हम सब करने के लिए छोड़ दिया है जवाब बंद पढ़ा है! ऐसा करने के लिए बस अपने मैट्रिक्स को समीकरणों के एक सेट में अनुवाद करें, और आप देखेंगे कि आपने x, y और z के लिए समाधान खोज लिए हैं।
1x+0y+0z =-1
0x+1y+0z=2
0x+0y+1z=-3 - सभी शून्य शर्तों को छोड़ने, आपको मिलता है:
x= -1
y= 2
z= -3 - इसका मतलब यह है कि 3-आयामी अंतरिक्ष में चौराहे बिंदु जहां तीन विमानों के बीच अंतर है (-1,2, -3)।
याद रखें कि आप हमेशा मूल समीकरणों में मानों को प्लग करके अपने समाधान की जांच कर सकते हैं - उपर्युक्त आर्टिकल में गाऊसी उन्मूलन का खेल:रैखिक बीजगणित का एक परिचय (The Game of Gaussian Elimination:An Introduction to Linear Algebra) के बारे में बताया गया है.
(The Game of Gaussian Elimination:An Introduction to Linear Algebra
गाऊसी उन्मूलन का खेल:रैखिक बीजगणित का एक परिचय
(The Game of Gaussian Elimination:An Introduction to Linear Algebra)
(The Game of Gaussian Elimination:An Introduction to Linear Algebra
गाऊसी उन्मूलन का खेल:रैखिक बीजगणित का एक परिचय (The Game of Gaussian Elimination:An Introduction to Linear Algebra)
में आव्यूह का प्रयोग किया गयाहै.गणित की विभिन्न शाखाओं में आव्यूह के ज्ञान की आवश्यकता पड़ती है.
आव्यूह,गणित के सर्वाधिक शक्तिशाली साधनों में से एक है.
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |