1.एक चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle),एक चिकने उर्ध्वाधर वृत के अन्त:तल की ओर कण की गति (Motion of a particle on inside of a smooth vertcle circle)-

एक चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle),एक चिकने उर्ध्वाधर वृत के अन्त:तल की ओर कण की गति (Motion of a particle on inside of a smooth vertcle circle) दिए हुए प्रतिबन्धों के अधीन होती है तो ऐसी गति को ‘प्रतिबन्धित गति (Constrained Motion)’ कहते हैं।प्रतिबन्धित गति का अध्ययन करने के लिए प्राय: स्पर्शरेखीय त्वरण तथा अभिलाम्बिक त्वरण का उपयोग करते हैं।
(1.)प्रतिबन्धित (व्यवरुद्ध) गति (Constrained Motion)-
परिभाषा (Definition):किसी कण की वह गति जिसमें कण किसी वक्र या पृष्ठ के सहारे चलने के लिए प्रतिबन्धित हो,कण की ऐसी गति को प्रतिबन्धित (व्यवरुद्ध) गति कहते हैं।जैसे किसी डोरी पर किसी मनके की गति अथवा किसी पृष्ठ या वक्र (गोला,चक्रज इत्यादि) के अन्दर या बाहर किसी कण की गति।

आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Tangential and normal components of acceleration

2.एक कण किसी चिकने समतल वक्र पर दिए हुए समतलीय बलों के अधीन चलने को बाध्य किया जाता है।इसकी गति की विवेचना करना।(A particle is made on a smooth plane curve under the motion of given coplanner forces.To discuss the motion of the particle.)

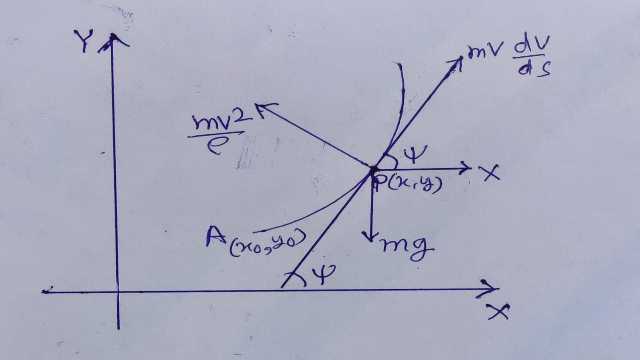
एक चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle),माना कि कण की संहति m है तथा यह भी माना कि t समय पर वक्र पर कण P पर है,बिन्दु P पर किसी स्थिर बिन्दु A से दूरी s है तथा P पर वेग v है।यह भी माना कि कण पर कार्य करने वाले बाह्य बलों का OX तथा OY की दिशा में क्रमशः घटक X तथा Y है। चूंकि वक्र चिकना है इसलिए कण पर बाह्य बलों के अतिरिक्त केवल अभिलम्ब प्रतिक्रिया R की ओर कार्य करेगी।
अब स्पर्श तथा अभिलम्ब की दिशा में कण की गति का समीकरण निम्न है:

m \frac{d^{2} s}{d t^{2}}=mv \frac{d v}{d s}=x \cos \psi+y \sin \psi \cdot \cdots(1)
तथा \frac{m v^{2}}{\rho}=R-x \sin \psi+y \cos \psi \ldots(2)
जहां \psi,P पर स्पर्शरेखा x-अक्ष के साथ कोण बनाता है।
समीकरण (1) से,m v \frac{d v}{d s}=x \cdot \frac{d x}{d s}+y \frac{d y}{d s} \\ \Rightarrow m v d v=x d x+y d y \\ \Rightarrow \frac{1}{2} m v^{2}=\int(x d x+y d y)+c
यदि Xdx+Ydy,फलन \phi(x, y) का पूर्ण अवकलन (Complete differentiation) है तो

x=\frac{\partial \phi}{\partial x}, y=\frac{\partial \phi}{\partial y} \\\frac{1}{2} m v^{2}=\int\left(\frac{\partial \phi}{\partial x} d x+\frac{\partial d}{\partial y} d y\right)+c=\phi(x, y)+c
यदि कण को A\left(x_{0}, y_{0}\right) से प्रक्षेप किया गया हो तथा इसका A पर वेग v_{0} हो तो

\frac{1}{2} m v_{0}^{2}=\phi \left(x_{0}, y_{0}\right)+c

अतः \frac{1}{2} m v^{2} -\frac{1}{2} m v_{0}^{2}=\phi(x, y)-\phi\left(x_{0}, y_{0}\right)
इससे स्पष्ट है कि कण की गतिज ऊर्जा में परिवर्तन कण की प्रारम्भिक तथा अन्तिम स्थिति अर्थात् A तथा P पर निर्भर करती है न कि उस पर जिस पर कण गमन करता है।किन्तु फलन \phi(x, y)=\int (x d x+y d y) बाह्य बलों द्वारा कण पर कार्य किया गया है तथा इसे कार्य फलन (Work Function) कहते हैं। ऐसे बल जिनके लिए विभव फलन का अस्तित्व है उन्हें अविनाशी बल (Conservative forces) कहते हैं।
अतः जब निकाय अविनाशी होता है तब
कण की गतिज ऊर्जा में परिवर्तन=बाह्य बलों द्वारा कण पर किया गया कार्य
उपर्युक्त सम्बन्ध को ऊर्जा समीकरण कहते हैं।
स्थितिज ऊर्जा (Potential Energy) को उस कार्य से परिभाषित किया जाता है जो कण अपनी स्थिति से मानक स्थिति में पहुंचने पर कार्य करता है।अब यदि कण की मानक स्थिति \left(x_{1}, y_{1}\right) हो तो
स्थितिज ऊर्जा (P.E.)= \int_{(x, y)}^{(x_{1}, y_{1})} (x d x+y d y) \\ [ \phi (x, y)]_{(x, y)}^{\left(x_{1}, y_{1}\right)} \\ =\phi \left(x_{1}, y_{1}\right)-\phi (x, y)
अब गतिज ऊर्जा+स्थितिज ऊर्जा (K.E.+P.E.)

=\frac{1}{2} m v_{0}^{2}+\phi(x, y)-\phi \left(x_{0}, y_{0}\right)+\phi\left(x_{1}, y_{1}\right)-\phi(x, y) \\ =\frac{1}{2} m v_{0}^{2}+\phi \left(x_{1}, y_{1}\right)-\phi\left(x_{0}, y_{0}\right)
अतः यदि एक बल निकाय अविनाशी हो तो स्थितिज ऊर्जा तथा गतिज ऊर्जा का योग पूर्ण गति में अचर होता है।

उपर्युक्त के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।

3.एक चिकने वक्र पर जो कि उर्ध्वाधर समतल में है, गुरुत्वाकर्षण के अधीन चलने वाले कण की गति (Motion of a paricle under gravity on a smooth curve in a vertical plane:)-

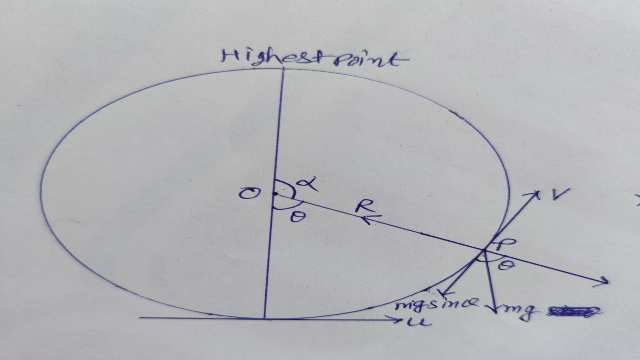
एक चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle),माना कि कण की संहति m है तथा यह भी माना कि t समय पर कण वक्र पर बिन्दु P पर है।यह भी माना कि वक्र का स्थिर बिन्दु A है।P की A से दूरी s है।मान लो कि P पर अभिलम्ब प्रतिक्रिया R है।यदि OX,OY निर्देशांकाक्ष क्षैतिज तथा उर्ध्वाधर दिशा में लें तो स्पर्शरेखा तथा अभिलम्ब की दिशा में कण के गति के समीकरण होंगे।

m \frac{d^{2} s}{d t^{2}} \equiv m v \frac{d v}{d s}=-m g \sin \psi-m g \frac{d v}{d s} \cdots(1)
तथा \frac{m v^{2}}{\rho}=R-m g \cos \psi=R-m g \frac{d x}{d s} .....(2)
जहां बिन्दु P पर स्पर्शरेखा,x-अक्ष के साथ \psi कोण बनाती है।
समीकरण (1) का समाकलन करने पर-

\frac{1}{2} m v^{2}=-m g y+c
यदि प्रारम्भ में y=y_{0},v=u तब

\frac{1}{2} m u^{2}=-m g y_{0}+c \\ \therefore \frac{1}{2} m v^{2}-\frac{1}{2} mu^{2}=-mg \left(y-y_{0}\right)=-mgh \cdots (3)
जहां h;बिन्दु P की बिन्दु A से ऊंचाई है।
समीकरण (3) को ऊर्जा समीकरण कहते हैं।
अब समीकरण (3) से समीकरण (2) में मान रखने पर-

R=\frac{m v^{2}}{\rho}+m g \cos \psi \\ =\frac{m}{\rho}\left\{u^{2}-2 g\left(y-y_{0}\right)\right\}^{2}+m g \cos \psi.....(4)
समीकरण (4) से किसी बिन्दु पर कण पर अभिलम्ब प्रतिक्रिया ज्ञात कर सकते हैं।कण वक्र कै छोड़ देगा जहां R=0, इसलिए

v^{2}=-g \rho \cos \psi

उपर्युक्त के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।

4.चिकने उर्ध्वाधर वृत्त या गोले के अन्त:तल की ओर गति (Motion of a paricle on inside of a smooth vertical circle or sphere)-

एक चिकने ऊर्ध्वाधर वृत्त के सबसे नीचे के बिन्दु से एक कण किसी वेग से फेंका गया जो वृत्त के अंदर की ओर गमन करता है।उसकी गति की विवेचना करना:
(A particle is projected from the lowest point with smooth vertical circle.To discuss the motion of the particle)
माना कि कण t समय पर कण की स्थिति P हैं,यदि वृत्त की त्रिज्या a तथा केन्द्र O हो तथा AOB उर्ध्वाधर व्यास हो तो माना \angle POA=\theta , यह भी मान लिया कि कण को वृत्त के सबसे नीचे वाले बिन्दु से u वेग से इस प्रकार प्रक्षिप्त (Project) किया कि वह वृत्त के अन्त:तल पर गति करता है।
कण पर केवल दो ही बाह्य बल कार्य करते हैं-(1)कण का भार mg उर्ध्वाधर नीचे की ओर (2) वृत्त की प्रतिक्रिया R,PO की दिशा में
यदि P पर कण का वेग v हो एवं P से OA पर PN लम्ब हो तो स्पर्शरेखा के अनुदिश कण की गति के लिए
गति के समीकरण से

mv \frac{d v}{d s}=-m g \sin \theta ...(1)

[वृत्त के लिए s=a \theta, \therefore \cdot d s=a d \theta]

r d v=-g \sin \theta d \theta
समाकलन करने पर-

\frac{1}{2} v^{2}=g a \cos \theta +c
प्रारम्भ में t=0,\theta=0 तथा v=u

\therefore c=\frac{1}{2} u^{2}-g a \\ \frac{1}{2} v^{2}=g a \cos \theta+\frac{1}{2} u^{2}-g a \\ v^{2}=u^{2}-2 g a+2 a g \cos \theta ...(2)
अथवा ऊर्जा समीकरण से-
गतिज ऊर्जा का अन्तर=बलों द्वारा किया गया कार्य

\frac{1}{2} m v^{2}-\frac{1}{2} m u^{2}=-m g \cdot A N \\ =-m g(a-a \cos \theta) \\ \Rightarrow v^{2}- u^{2}=-2 g a(1-\cos \theta) \\ \Rightarrow v^{2}=u^{2}-2 a g+2 a g \cos \theta....(2)
अभिलम्ब दिशा में कण की गति का समीकरण:

\frac{m v^{2}}{a}=R-m g \cos \theta [\because \rho=a ] \\ \Rightarrow R=\frac{m}{a}\left[v^{2}+g a \cos \theta\right] [अब (2) से का मान रखने पर]

=\frac{m}{a}\left[u^{2}+3 g a \cos \theta-2 g a\right]...(3)
इससे R का मान बिन्दु P पर किसी समय t पर प्राप्त होता है।
अब यदि \theta=\theta_{1} पर v=0 तो समीकरण (2) से-

u^{2}=2 g a(1-\cos \theta)\\ \Rightarrow \cos \theta_{1}=\frac{2 a g-u^{2}}{2 a g}....(4)
तथा साथ ही यदि \theta=\theta_{2} पर R=0 तो समीकरण (3) से-

\theta=\frac{m}{a}\left[u^{2}+3 g a \cos \theta_{2}-2 g a\right] \\ \Rightarrow \cos \theta_{2}=\frac{2 a g-u^{2}}{3 a g}....(5)
हम नीचे कण की गति का विभिन्न अवस्थाओं में अध्ययन करेंगे:
अवस्था I.यदि R से पहले v लोप हो जाए (If v vanishes before R vanishes):
इस अवस्था में \theta_{1}<\theta_{2} \\ \Rightarrow \cos \theta_{1}>\cos \theta_{2} \\ \Rightarrow \frac{2 a g-u^{2}}{2 a g}>\frac{2 a g-u^{2}}{3 a g} \\ \Rightarrow u^{2}<2a g
अब यदि u^{2}<2 a g लें तो \cos \theta_{1} का मान धनात्मक है अतः \cos \theta_{1}>0 \Rightarrow \theta_{1}<90^{\circ} अर्थात् कण क्षैतिज व्यास तक नहीं पहुंचता है।इस स्थिति में कण क्षणभर के लिए विरामावस्था में आकर पथ पर नीचे की ओर वापिस चलना प्रारम्भ कर देता है और क्योंकि कण का वेग सबसे नीचे बिन्दु A पर धनात्मक है इसलिए A से दूसरी ओर चलने लगता है।साथ ही यदि समीकरण (2) तथा (3) के स्थान पर -\theta_{1}रखते हैं तो समीकरण नहीं बदलता है। अतः उर्ध्वाधर व्यास के दोनों ओर कण की गति एक-समान है।
इस प्रकार कण की गति उर्ध्वाधर व्यास के दोनों ओर दोलनीय (Ok scillatory) होती है।
अवस्था II.R तथा v साथ-साथ लोप होते हैं (R and v vanish simultaneously):
इस अवस्था में \theta_{1}=\theta_{2} \Rightarrow \cos \theta=\cos \theta_{2} \\ \Rightarrow \frac{2 a g-u^{2}}{2 a g}=\frac{2 a g-u^{2}}{3 a g} \Rightarrow u^{2}=2 a y \quad[\because a g \neq 0]
साथ ही u^{2}=2 a g^{2} के लिए \cos \theta_{1}=\cos \theta_{2}=0 अर्थात् \theta_{1}=\theta_{2}=\frac{\pi}{2} इससे यह प्रदर्शित होता है कि कण क्षैतिज व्यास तक जाता है तथा क्षणभर के लिए विराम अवस्था में आकर अपने पथ पर नीचे की ओर वापिस चलना प्रारम्भ कर देता है क्योंकि कण का वेग निम्नतम बिन्दु A पर धनात्मक है इसलिए वह A के दूसरी ओर चलने लगता है तथा कण की गति उर्ध्वाधर व्यास के दोनों ओर दोलनीय (R vanishes before v vanishes):
इस अवस्था में \theta_{1} > \theta_{2} \\ \Rightarrow \cos \theta_{1}<\cos \theta_{2} \\ \Rightarrow \frac{2 a g-u^{2}}{2 a g}<\frac{2 a g-u^{2}}{3 a g} \\ \Rightarrow u^{2}>2 a g
u^{2}>2 a g के लिए \cos \theta_{2} ऋणात्मक है। अतः \theta_{2} अधिक कोण (>90°) है।
अतः कण क्षैतिज व्यास के सिरे से ऊपर जाता है तथा \theta=\theta_{2}पर कण वृत्त को छोड़ देता है तथा गुरुत्वाकर्षण के अधीन परवलीय पथ का अनुसरण करता है।
अवस्था IV.वृत्त या गोले का पूरा चक्कर लगाने का प्रतिबंध (Condition for tracing the complete curcle or sphere)
कण वृत्त या गोले का पूरा चक्कर लगाएगा यदि सर्वोच्च बिन्दु B (जहां है) पर कण का वेग तथा वृत्त की प्रतिक्रिया दोनों धनात्मक तथा वास्तविक (Real and positive) हों अर्थात् v>0,R>0 अर्थात्

u^{2}-2 a g+2 a g \cos \pi>0 \Rightarrow u^{2}>>4 a g
तथा \frac{m}{a} \cdot\left(u^{2}-2 a g+3 a g \cos \pi\right)>0 \Rightarrow u^{2}>5 a g
उपर्युक्त से स्पष्ट है कि यदि u^{2}>5 a g हो तो B पर v>0,R>0 तथा वास्तविक होंगे। अतः यदि u^{2}>5 a g तो कण वृत्त का पूरा चक्कर लगाएगा।
यदि u^{2}=5 a g तो बिन्दु B पर v>0 परन्तु R=0
अतः इस अवस्था में R तो क्षणभर के लिए शून्य होगा परन्तु कण वृत्त का पूरा चक्कर लगाएगा।
(1.)उपप्रमेय (Cor) 1.यदि कण को निम्नतम बिन्दु A से वृत्त के अन्त:तल में एक ऐसे वेग से प्रक्षिप्त किया जाए कि वह ठीक वृत्त के सर्वोच्च बिन्दु B तक पहुंच सके तो निम्नतम बिन्दु A पर दबाव 6mg अर्थात् कण के भार के छ: गुणा होता है।
(If the particle is projected with a Velocity just sufficient to take it to the height point, pressure at the lowest point is 6mg i.e. six times the weight of the particle.)
उपर्युक्त से हम जानते हैं कि यदि कण का निम्नतम बिन्दु A पर वेग u,जबकि u^{2}=5 a g हो तो वह वृत्त के सर्वोच्च या शीर्ष बिन्दु तक पहुंचता है।
अतः किसी भी बिन्दु पर वृत्त की कण पर प्रतिक्रिया

R=\frac{m}{a}\left(u^{2}-2 a g+3 a g \cos \theta\right)
अब u^{2}=5 a g तथा बिन्दु A पर \theta =0 \\ \therefore R_{A}=\frac{m}{a}(5 a g-2 a g+3 a g)=6 m g
(2.)यदि कण वृत्त का पूरा चक्कर लगाता है तो किसी भी वृत्त के सिरो पर दबाव का योग अचर होता है।
(If the particle goes right round a circle,the sum of the pressure at the ends of any diameter is constant.)
वृत्त के किसी बिन्दु पर दबाव R

R=\frac{m}{a} \left(u^{2}-2 a g+3 ag \cos \theta  \right)
वृत्त के किसी भी व्यास के सिरों पर दबाव का योग

=\frac{m}{4}\left[u^{2}-2 ag+3 a g \cos \theta \right]+\frac{m}{a}\left[u^{2}-2 a g+3 a g \cos (\theta+\pi)\right] \\=\frac{m}{a} \left[2 u^{2}-4 a g\right]
क्योंकि वह पर निर्भर नहीं है, अतः अचर है।
टिप्पणी 1.यदि किसी कण को डोरी से बांधकर किसी बिन्दु से लटकाया जाए तो कण वृत्त में गति करेगा तथा R के स्थान पर डोरी का तनाव T आ जाएगा तथा कण की गति का शेष विवेचन यथापूर्व ही होगा।
यदि 2 a g<u^{2}<5 a g तो \theta के किसी मान (>90°) के लिए रस्सी ढीली पड़ जाती है और फिर कण गुरुत्वाकर्षण के अधीन वृत्तीय पथ को छोड़कर एक परवलय पथ का अनुसरण करता है जब तक कि डोरी फिर न तन जाए।
टिप्पणी 2.यदि कोई कण किसी ट्यूब में गमन करे या मनका एक वृत्तीय तार पर गमन करे तो चूंकि प्रतिक्रिया अन्दर या बाहर दोनों ओर हो सकती है। अतः इस अवस्था में R कभी भी विलोप नहीं होगा तथा कण सदैव वृत्तीय पथ में ही गमन करेगा।फलत: पूरे वृत्त के चक्कर लगाने के लिए u^{2}>4 a g प्रतिबन्ध ही पर्याप्त होगा।

उपर्युक्त के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।

5.एक चिकने उर्ध्वाधर वृत्त के अन्दर गति के उदाहरण (Motion inside a smooth vertical circle Examples),एक चिकने उर्ध्वाधर वृत्त के अन्त:तल की ओर कण की गति के उदाहरण (Motion of a particle on inside of a smooth vertcle circle Examples)-

Example-1.कोई कण ‘a’ त्रिज्या के एक चिकने ऊर्ध्वाधर वृत्त के अन्त:तल के साथ वृत्त के सबसे नीचे के बिन्दु से वेग \frac{1}{5} \sqrt{(95 a g)}  से प्रक्षिप्त किया जाता है। सिद्ध करो कि वह सर्वोच्च बिन्दु से \cos ^{-1}(3 / 5) कोणीय दूरी पर वृत्त से सम्पर्क छोड़ देगा और उस समय उसका वेग \frac{1}{5} \sqrt{(15 a g)}होगा।
(A particle is projected along the inner surface of a smooth vertical circle of radius a ,its velocity at the lowest point being \frac{1}{5} \sqrt{(95 a g)} .Show that it will leave the circle at an angular distance \cos ^{-1}(3 / 5) from the highest point and its velocity is \frac{1}{5} \sqrt{(15 a g)}.)
Solution– वृत्त की त्रिज्या a है तथा कण को निम्नतम बिन्दु से वेग से प्रक्षिप्त किया जाता है तो कण के गति समीकरण होंगे-

mv \frac{d v}{d s}=-m g \sin \theta\cdots(-1)
तथा m \frac{v^{2}}{a}=R-m g \sin \theta....(2)
वृत्त के लिए S=a \theta \Rightarrow d s=a d\theta

अब समीकरण (1) का समाकलन करने पर-

v^{2}=2 g a \cos \theta+A
प्रारम्भ में \theta=0, v=u \quad \therefore A=u^{2}=2 a g
अतः v^{2}=u^{2}-2 a g+2 g a \cos \theta...(3)
समीकरण (3) से v^{2} का मान (2) में रखने पर-

R=\frac{m}{9}\left(u^{2}-2 a g+3 a g \cos \theta\right) \cdots(4) \\ u=\frac{1}{5} \sqrt{95 g a} (given)\\ u^{2}=\frac{9 5 g a}{25} \Rightarrow u^{2}=\frac{19g a}{5}
कण वृत्तीय पथ को छोड़ देगा जब R= 0
समीकरण (4) से-

0=\frac{m}{a}\left(u^{2}=2 a g+3 a g \cos \theta\right) \\ \cos \theta=-\frac{u^{2}-2 g a}{3 a g} \\ \Rightarrow \cos \theta=-\frac{1}{3 a g}\left(\frac{19 a g-10 g a}{5}\right) \\ \Rightarrow \cos \theta=(-3 / 5) \\ \Rightarrow \cos \alpha=\cos (\pi-\theta)=-\cos \theta \\ \Rightarrow \cos \alpha=3 / 5 \Rightarrow \alpha=\cos^{-1} (3 / 5)
अतः सर्वोच्च बिन्दु से कोणीय दूरी \alpha=\cos^{-1} (3 / 5)
समीकरण (3) से- v^{2}=u^{2}-2 g a+2 g a \cos \theta \\ \Rightarrow v^{2}=\frac{19}{5} ga -2 ga +2 ga \cos \left(\cos ^{-1}(-3 / 5)\right) \\ \Rightarrow v^{2}=\frac{19}{5} ga-2 g a+2 g a (\frac{-3}{5}) \\ \Rightarrow v^{2}=\frac{19ga-10 g a-6ga}{5} \\ \Rightarrow v^{2}=\frac{3 g a}{5} \\ \Rightarrow v^{2}=\frac{15 a g}{25} \\ \Rightarrow \quad v=\frac{1}{5} \sqrt{(15 a g)}

उपर्युक्त उदाहरण के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।
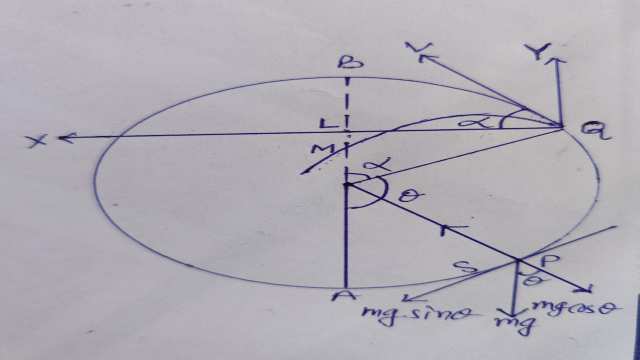
Example-2.एक कण a त्रिज्या के एक चिकने वृत्त के अन्त:तल के साथ वृत्त के सबसे नीचे के बिन्दु से ऐसे वेग से प्रक्षिप्त किया जो कि वह केन्द्र से h ऊंचाई से गिरने पर अर्जित करता है।वह बिन्दु ज्ञात कीजिए जहां कण वृत्त से सम्पर्क छोड़ देगा तथा यह सिद्ध कीजिए कि इसके उपरान्त यह (a)केन्द्र से गुजरेगा यदि h=\frac{a \sqrt{3}}{2}, (b) निम्निष्ठ बिन्दु से गुजरेगा यदि h=\frac{3a}{4}
(A particle is projected from the lowest point inside a smooth circle of radius a with a velocity due to a height h above the centre.Find the point where it leaves the circle and show that it will afterwards pass through (a) centre,if h=\frac{a \sqrt{3}}{2} and (b) the lowest point if h=\frac{3a}{4})
Solution-गति के समीकरण होंगे

v^{2}=u^{2}-2 a g+2 g a \cos \theta....(1) \\ R=\frac{m}{a}\left(u^{2}-2 a g+3 a g \cos \theta\right)..(2)
केन्द्र से h ऊंचाई से गिरने के पर अर्थात् a+h ऊंचाई से गिरने पर वेग प्रक्षेप वेग के समान हैं अतः

u^{2}=2 g(a+h)\cdots(3)
कण वृत्तीय पथ को छोड़ देगा यदि तनाव R=0

0=\frac{m}{a}\left[u^{2}-2 a g+3 a g \cos \theta\right] \\ \therefore \cos \theta=-\frac{u^{2}-2 a g}{3ag} \\ \Rightarrow \cos \theta=-\left[\frac{2 g(a+h)-2 a g}{3 a g}\right] \\ \Rightarrow \cos \theta=-\left[\frac{2 g h}{3 a g}\right] \\ \Rightarrow \cos \theta=-\frac{2 h}{3 a}[(2) व (3)से]

\Rightarrow \cos \alpha=\cos (\pi-\theta)=-\cos \theta \\ \Rightarrow \cos \alpha=\frac{2 h}{3 a}
जहां कोण \alpha,बिन्दु Q पर वेग द्वारा क्षैतिज के साथ दिशा है

\therefore v^{2}=u^{2}-2 a g+2 a g \cos \theta \\ \Rightarrow v^{2}=2 g a+2 g h-2 a g+2 g a \left(-\frac{2 h}{3 a}\right) \\ \Rightarrow v^{2}=\frac{2}{3} g h...(5)
कण द्वारा तय किया गया परवलयिक समीकरण

y=x \tan \alpha-\frac{1}{2} g \frac{x^{2}}{v^{2} \cos ^{2} \alpha} \ldots(6)

यदि यह केन्द्र C से गुजरे तो इसके निर्देशांक (PN,-CN)
या (a \sin \alpha ,-a \cos \alpha)
-a \cos \alpha=a \sin \alpha.\tan \alpha-\frac{1}{2} g \frac{a^{2} \sin ^{2} \alpha}{\frac{2}{3} g h \cos ^{2} \alpha} [(5)से]

\Rightarrow \frac{3}{4} \frac{a}{h} \frac{ \sin ^{2} \alpha}{\cos ^{2} \alpha}=\sin \alpha \cdot \frac{\sin \alpha}{\cos \alpha}+\cos \alpha \\ \Rightarrow \frac{3 a}{4 h} \frac{\sin ^{2} \alpha}{\cos ^{2} \alpha} =\frac{1}{\cos \alpha} \\ \Rightarrow 3 a\left(1-\cos ^{2} \alpha\right)=4 h \cos \alpha \\ \Rightarrow 3 a\left[1-\frac{4 h^{2}}{9 a^{2}}\right]=4 h \cdot \frac{2 h}{3 a} \\ \Rightarrow 3 a=\frac{4 h^{2}}{3 a}+\frac{8 n^{2}}{3 a} \\ \Rightarrow 3 a=\frac{4 h^{2}}{a} \\ \Rightarrow h^{2}=\frac{3 a^{2}}{4} \Rightarrow h=\left(\frac{\sqrt{3} a}{2}\right)
(b) निम्नतम बिन्दु A है

[a \sin \alpha,-(a+a \cos \alpha)] समीकरण (6)  में रखने पर-

-(a+a \cos \alpha)=a \sin \alpha \cdot \tan \alpha-\frac{1}{2} g \frac{a^{2} \sin ^{2} \alpha}{\frac{2}{3} g h \cos ^{2}} \\ \Rightarrow \frac{3}{4} \frac{ \cdot \operatorname{asin}^{2} \alpha}{h \cos ^{2} \alpha} =\sin \alpha \cdot \frac{\sin \alpha}{\cos \alpha}+\cos \alpha+1 \\ \Rightarrow \frac{3}{4} \frac{\sin^{2} \alpha}{h \cos ^{2} \alpha}=\frac{1+\cos \alpha}{\cos \alpha} \\ \Rightarrow 3 a(1-\cos \alpha)(1+\cos \alpha)=4 h \cos \alpha(1+\cos \alpha) \\ \Rightarrow 3 a\left(1-\frac{2 h}{3 a}\right)=4 h \cdot \frac{2 h}{3 a} \quad[\because \cos \alpha \neq-1] \\ \Rightarrow 3 a=2 n+\frac{8 h^{2}}{3 a} \\ \Rightarrow 8 h^{2}+6 a h-9 a^{2}=0 \\ \Rightarrow h=\frac{-6 a \pm \sqrt{36 a^{2}+288 a^{2}}}{16} \\\Rightarrow h=\frac{-6 a+18 a}{16} \\ \Rightarrow h=\frac{3 a}{4}

उपर्युक्त उदाहरण के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।
Example-3. (a.) एक m द्रव्यमान का भारी कण l लम्बाई की डोरी से उर्ध्वाधर दिशा में लव लटकाया गया है।तत्पश्चात् इसको u वेग से प्रक्षिप्त किया जाता है और यह ठीक एक पूर्ण परिक्रमा लगाता है।सिद्ध करो कि u^{2}=5 g l तथा निम्नतम बिन्दु पर डोरी में तनाव ज्ञात कीजिए।
(A heavy particle of mass m is suspended by a string of length l and hangs vertically;it is then projected with velocity u so that it just make a complete revolution.Show that u^{2}=5 g l.Find also the tension at the lowest point.)
(b.) एक भारी कण एक बिन्दु O से a लम्बाई की एक डोरी द्वारा लटक रहा है।इसे क्षैतिज वेग u से विस्थापित किया जाता है।यदि u^{2}=(2+\sqrt{3})ag;तो सिद्ध कीजिए कि डोरी \cos (- \frac{1}{\sqrt{3}}) कोण बनाने के पश्चात् शिथिल हो जाएगी।
(A heavy particle hangs from a point O by a string of lengths a.If is projected horizontally with velocity such that u^{2}=(2+\sqrt{3})ag; Show that the string becomes slack when it happened has described an angle \cos (- \frac{1}{\sqrt{3}}).)
Solution-(a.) गति के समीकरण होंगे-

v^{2}-u^{2}-2 a g+2 a g \cos \theta....(1) \\ R=\frac{m}{a} \left[u^{2}-2 g a+3 a g \cos \theta \right]....(2)
यदि कण वृत्त का पूरा चक्कर लगाता है तो उच्चत्तम बिन्दु पर T=0

0=\frac{m}{u} \left[u^{2}-2 g l+3 \lg \cos 180^{\circ}\right] \\ \Rightarrow u^{2}=5 l g
समीकरण (2) में रखने पर-

T =\frac{m}{l}[5g l-2 g l+3 g l \cos \theta] \\ =\frac{m}{l}\left[3 g l+3 g l \cos \theta\right] \\ =3 m g(1+\cos \theta)
निम्नत्तम बिन्दु पर \theta=0 \\ T=3 m g(1+\cos \theta) \\ T=3 m g(1+1) \\ T=6 m g
(b.) डोरी शिथिल हो जाएगी जब T=0 तथा दिया हुआ है कि 

u^{2}=(2+\sqrt{3}) a g
अतः समीकरण (2) में मान रखने पर-

0 =\frac{m}{u} \left[u^{2}-2 g a+3 a g \cos \theta \right] \\ \Rightarrow (2+\sqrt{3}) a g-2 a g+3 a g \cos \theta =0 \\ \Rightarrow 2 a g+\sqrt{3} a g-2 a g+3 a g \cos \theta=0 \\ \Rightarrow \sqrt{3} a g+3 a g \cos \theta=0 \\ \Rightarrow \sqrt{3} a g(1+\sqrt{3} \cos \theta)=0 \\ \Rightarrow \sqrt{3} \cos \theta=0 \\ \Rightarrow \cos \theta =\left(-\frac{1}{\sqrt{3}}\right) \Rightarrow \theta=\cos ^{-1}\left(-\frac{1}{\sqrt{3}}\right)

उपर्युक्त उदाहरण के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।
Example-4. एक भारी कण किसी स्थिर बिन्दु से एक डोरी जिसकी लम्बाई l है द्वारा लटकाया हुआ है और वह उर्ध्वाधर वृत्त में घूमता है। सिद्ध कीजिए कि किसी भी व्यास के सम्मुख सिरों पर डोरी के तनावों का योग सभी व्यासों के लिए समान होता है।
(A heavy particle hanging vertically from a point by a light inextensible string of length l is started so as to make a complete revolution in a vertical plane.Prove that the sum of the tensions at the ends of any diameter is constant.)
Solution– गति के समीकरण होंगे-

v^{2}=u^{2}-2 g a+2 g a \cos \theta...(1) \\ T=\frac{m}{a}\left[u^{2}-2 g a+3 g a \cos \theta\right]....(2)
माना कि कोई भी व्यास लम्ब के साथ \alpha कोण बनाता है,तब हमें \theta= \alpha तथा \theta =180+ \alpha पर तनावों का योग ज्ञात करना है-
T_{1}=\frac{m}{a} \left[ u^{2}-2 a g+2 a g \cos \alpha\right][समीकरण (2) से]…(3)

T_{2}=\frac{m}{a}\left[u^{2}-2 a g+2 a g \cos (180+\alpha)\right]....(4)
समीकरण (3) व (4) का योग करने पर-

T_{1}+T_{2}=\frac{m}{a}\left[u^{2}-2 a g+2 a g \cos \alpha+u^{2}-2 a g+2 a g \cos (180+\alpha)\right] \\ \Rightarrow T_{1}+T_{2}=\frac{m}{a}\left[2 u^{2}-4 a g+2 a g \cos \alpha-2 a g \cos \alpha\right] \\ \Rightarrow T_{1}+T_{2}=\frac{m}{a} (2u^{2}-4 a g)

जो कि \alpha पर निर्भर नहीं करता है

उपर्युक्त उदाहरण के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।
Example-5. एक भारी कण जो कि a लम्बाई की डोरी द्वारा किसी नियत बिन्दु से लटका हुआ है,यदि इस कण को क्षैतिज दिशा में \sqrt{6})ag वेग से प्रक्षिप्त किया जाता है। सिद्ध कीजिए डोरी का उस स्थिति में तनाव जबकि कण क्षैतिज व्यास के सिरे पर होता है,उस तनाव से जबकि वह उच्चत्तम बिन्दु पर होता है,4:1 का अनुपात रखता है।
(A particle hanging vertically from a fixed point by means of a string of length a is projected horizontally with velocity \sqrt{6})ag .Prove that the tension of the string when the particle is at the end of a horizontal diameter is to its tension when the particle is at the highest point as 4:1.)
Solution– गति के समीकरण होंगे-

v^{2}=u^{2}-2 a g+2 g a \cos \theta ...(1) \\ T=\frac{m}{a}\left[u^{2}-2 g a+3 g a \cos \theta\right]...(2)
समीकरण (2) में क्षैतिज व्यास के लिए \theta =90° तथा u^{2}=6 a g रखने पर-

T_{1}=\frac{m}{a}[6 a g-2 a g+3 a g \cos 90^{\circ}] \\ \Rightarrow T_{1}=\frac{m}{a}[4 a g+0] \\ T_{1}=4mg

उच्चत्तम बिन्दु \theta =180° रखने पर-

T_{2} =\frac{m}{a}\left[6 a g-2 a g+3 a g \cos \left(180^{\circ}\right)\right] \\ =\frac{m}{a}[4 a g-3 a g] \\ =\frac{m}{a} \times a g \\ T_{2} =m g \\ T_{1}:T_{2}=4 m g:m g \\ T_{1}:T_{2}=4:1

उपर्युक्त उदाहरण के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।
Example-6. एक झूले के रस्से स्थिर अवस्था में किसी व्यक्ति के भार के दुगुने के समान तनाव सहन कर सकते हैं तो सिद्ध करो कि वह व्यक्ति इस पर 120° कोण तक दोलन कर सकता है।
यदि रस्सियां इतनी मजबूत हो कि वह 180° के कोण में होकर झूल सकता है और किसी बिन्दु पर उसका वेग v हो तो सिद्ध करो कि उस बिंदु पर रस्सी का तनाव \frac{3 m v^{2}}{2 a} होगा, जहां m पुरुष की संहति और a रस्सी की लम्बाई है।
(Show that the greatest angle through which a person can osciliate on a swing the ropes of which can support twice the person’s weight at rest is 120°.If the ropes are strong enough so that he can swing through 180° and if v is his speed at any point,prove that the tension in the rope at that point is \frac{3 m v^{2}}{2 a} ;where m is the mass of the person and a the length of the rope.)
Solution– गति के समीकरण होंगे-

v^{2}=u^{2}-2 a g+2 a g \cos \theta.....(1) \\ T=\frac{m}{a}\left[u^{2}-2 g a+3 g a \cos \theta\right]...(2)
निम्नत्तम बिन्दु अर्थात् पर तनाव T अधिकतम होगा

\therefore T_{0}=\frac{m}{a}\left[u^{2}-2 a g+3 a g \cos \theta \right] \\ \Rightarrow 2 m g=\frac{m}{a}\left[u^{2}-2 a g+3 a g\right] \\ \Rightarrow 2 a g=u^{2}+a g \Rightarrow u^{2}=a g
जहां वेग शून्य होगा वहां कोणीय दूरी ज्ञात का करना है-
अतः समीकरण (1) से-

0=a g-2 a g+2 a g \cos \theta \\ \Rightarrow \cos \theta=\frac{a g}{2 a g} \Rightarrow \cos \theta=\frac{1}{2} \\ \Rightarrow \theta=60^{\circ}
अतः व्यक्ति 60° कोण दूरी ऊपर की ओर तथा 60° दूसरी तरफ झूलता है।इस प्रकार वह उच्चत्तम बिन्दु कोणीय दूरी 120° तक झूल सकता है।
अब दूसरे भाग में 180° कोण में होकर झूलने के लिए \theta =90° तथा v=0 तब समीकरण (1) से-

0=u^{2}-2 a g+2 a g \cos 90^{\circ} \\ \Rightarrow u^{2}=2 a g
u^{2}=2 a g समीकरण (1) में रखने पर-

v^{2}=2 a g-2 a g+2 a g \cos \theta \\ v^{2} = 2 a g \cos \theta \Rightarrow \cos \theta=\frac{v^{2}}{2 a g}
अतः समीकरण (2) में \cos \theta=\frac{v^{2}}{2 a g} तथा u^{2}=2 a g रखने पर-

T=\frac{m}{a}\left[2 a g-2 a g+3 a g \cdot \frac{v^{2}}{2 a g}\right] \\ \Rightarrow T=\frac{m}{a} \cdot \frac{3 v^{2}}{2} \Rightarrow T=\frac{3 m v^{2}}{2 a}

उपर्युक्त उदाहरण के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।
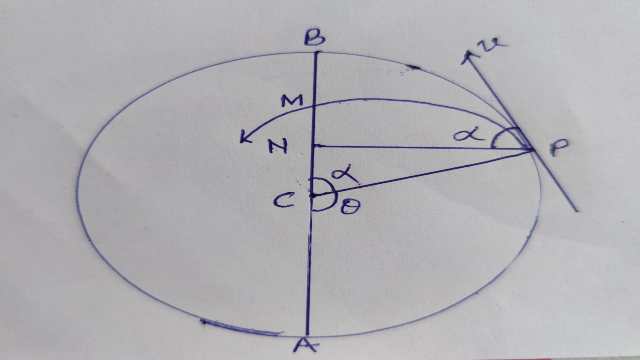
Example-7.एक कण लम्बाई की रस्सी से किसी स्थिर बिन्दु से लटकाया जाता है।l ऊंचाई से गिरने में जो कण वेग ग्रहण करता है उसके k गुणा से कण को क्षैतिज दिशा में प्रक्षिप्त किया जाता है।यदि कण वृत्तीय पथ को छोड़ देता है तो सिद्ध कीजिए कि कण निम्नत्तम बिन्दु से \left(\frac{l}{3}\right)\left(1+2 k^{2}\right) ऊंचाई पर वृत्तीय पथ छोड़ेगा साथ ही सम्पूर्ण कण अपनी गति में कितनी सर्वोच्च ऊंचाई तक जाता है,ज्ञात कीजिए।
(A particle at the end of a string of length l, the upper end of which is fixed is up projected horizontally with a velocity which is k times that due to a fall l.If the particle leaves the circular path z show that it does so at a height \left(\frac{l}{3}\right)\left(1+2 k^{2}\right)  above of the lowest point.Also find the greatest height that the particle attains during the entire motion.)
Solution- l ऊंचाई से गिरने पर कण का वेग=\sqrt{2 g l}
अतः प्रक्षेप वेग u^{2}=2 k^{2} g l \\ \cos \alpha=\frac{u^{2}-2 g l}{3 g e}=\frac{2}{3}\left(k^{2}-1\right)
तथा v^{2}=\frac{u^{2}-2 g l}{3}=\frac{2}{3} g l\left(k^{2}-1\right)

अतः सर्वोच्च बिन्दु की निम्नत्तम बिन्दु से ऊंचाई

A N =l+l \cos \alpha=l \left[1+\frac{2}{3}\left(k^{2}-1\right)\right] \\ =\frac{l}{3}\left(1+2 k^{2}\right)
महत्तम ऊंचाई P के ऊपर \frac{v^{2} \sin ^{2} \alpha}{2 g} \\ NM=\frac{v^{2}}{2 g}\left(1-\cos ^{2} \alpha\right) \\ =\frac{v^{2}}{2 g}(1-\cos \alpha)(1+\cos \alpha) \\ =\frac{v^{2}}{2 g}\left[1-\frac{2}{3}\left(k^{2}- 1\right)\right] \left[ 1+\frac{2}{3}\left(k^{2}-1\right)\right] \\ =\frac{v^{2}}{2 g}\left[\frac{3-2 k^{2}+2}{3}\right] \left[\frac{3+2 k^{2}-2}{3}\right] \\ =\frac{v^{2}}{2 a}\left[\frac{5-2 k^{2}}{3}\right]\left[\frac{1+2 k^{2}}{3}\right]=\frac{l}{3}\left(k^{2}-1\right)\left(\frac{5-2 k^{2}}{3}\right)\left(\frac{1+2 k^{2}}{3}\right)
अतः निम्नत्तम बिन्दु से ऊंचाई

AN+NM=\frac{l}{3}\left(1+2 k^{2}\right)+\frac{l}{27}\left(k^{2}-1\right)\left(5-2 k^{2}\right)(1+2 k^{2}) [(1)से ]

=\frac{l}{3}\left(1+2 k^{2}\right)\left(9+5 k^{2}-5-2 k^{4}+2 k^{2}\right) \\ =\frac{l}{3}\left(1+2 k^{2}\right)\left(4+7 k^{2}-2k^{4}\right) \\ =\frac{l}{3}\left(1+2 k^{2}\right)\left(1+2 k^{2}\right)\left(4-k^{2}\right) \\ =\frac{l}{3}\left(1+2 k^{2}\right)^{2}\left(4-k^{2}\right)
Example-8. एक कण किसी स्थिर खूंटी O से एक डोरी,जिसकी लम्बाई l है,लटकाई हुई है।कण को इतना ऊपर उठाया कि डोरी क्षैतिज हो जाए तथा छोड़ दिया जाए। सिद्ध कीजिए कि जब डोरी क्षैतिज के साथ \theta कोण बनाती है तब कण का परिणामी त्वरण g \sqrt{\left(1+3 \sin ^{2} \theta\right)} है।
(A particle attached to a fixed O by a string of length l is lifted up with the string taut horizontal and then let go.Prove that when the string makes an angle \theta with the horizontal,the resultant acceleration is g \sqrt{\left(1+3 \sin ^{2} \theta\right)}.)
Solution– गति का समीकरण-

m\frac{ d^{2} s}{d t^{2}}=m y \cos \theta \\ \Rightarrow v \frac{d v}{d s}=g \cos \theta \\ \Rightarrow v d v=g \cos \theta \frac{d s}{d \theta} d \theta \\ \Rightarrow v dv=ag \cos \theta d \theta \quad\left[s=a \theta \Rightarrow \frac{d s}{d \theta}=a\right] \\ \Rightarrow a=l \\ \Rightarrow v d v=al \cos \theta d \theta

समाकलन करने पर-

v^{2}=2 g l \sin \theta +A
जब \theta=0 तो v=0,A=0

v^{2}=2 g l \sin \theta
अभिलाम्बिक त्वरण=\frac{v^{2}}{\rho}=\frac{v^{2}}{l} \\ =\frac{2 g l \sin \theta} {l} \\ =2 g \sin \theta

परिणामी त्वरण=\sqrt{\left\{(T. A)^{2}+(N. A)^{2}\right\}} \\ \sqrt{\left(\frac{d^{2} s}{d t^{2}}\right)^{2} +\left(\frac{v^{2}}{\rho}\right)^{2}} \\ \sqrt{(g \cos \theta)^{2}+(2g \sin \theta)^{2}} \\ =g \sqrt{\cos ^{2} \theta+4 \sin ^{2} \theta} \\ g \sqrt{1+3 \sin ^{2} \theta}

उपर्युक्त उदाहरणों के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।

6.एक चिकने ऊर्ध्वाधर वृत्त के अन्दर गति की समस्याएं (Motion inside a smooth vertical circle Problems),एक चिकने ऊर्ध्वाधर वृत्त के अन्त:तल की ओर गति की समस्याएं (Motion of a particle on inside of a smooth vertcle circle Problems)-

(1.) कोई कण एक स्थिर गोले के अन्त:तल के साथ गोले के सबसे नीचे बिन्दु से उतने वेग से प्रक्षिप्त किया जाता है जितना वेग उस कण को उर्ध्वाधर व्यास पर स्वतन्त्र रूप से गिरने पर होगा। सिद्ध कीजिए कि कण गोले को छोड़ देगा तथा तत्पश्चात् प्रक्षेप बिन्दु के ऊपर से व्यास \frac{25}{32} के दूरी की ऊंचाई से गुजरेगा।
(A particle is projected along the inside of a smooth fixed sphere from its lowest point with a velocity equal to that due to falling freely down the vertical diameter of the sphere.Show that the particle will leave the sphere and afterwards pass vertically over the point of projected at a distance equal to \frac{25}{32} of the diameter.)
(2.) एक कण 1 मीटर लम्बी एक अप्रत्यास्थ डोरी के सिरे से बंधा है।उसे ऐसे प्रारम्भिक क्षैतिज वेग से चलाया जाता है कि डोरी ढ़ीली पड़ जाती है,जब कण निम्नत्तम \frac{5}{3} बिन्दु से मीटर ऊंचा है। सिद्ध करो कि वह \frac{5}{27}  मीटर ओर ऊंचा जाएगा।
(A particle is hanging from a fixed point by a light inelastic cord 1 m long and has started moving with an initial horizontal velocity such that the cord slackens when the particle is \frac{5}{3} m above the lowest point.Show that it will rise further through \frac{5}{27} m.)
(3.) एक भारी कण किसी बिन्दु से एक भारहीन a लम्बाई की अवितान्य रस्सी द्वारा उर्ध्वाधर दिशा में लटक रहा है।वह \sqrt{2}gh वेग से क्षैतिज दिशा में प्रक्षिप्त किया जाता है।यदि \frac{5}{2}a>h>a, सिद्ध कीजिए कि वृत्तीय गति उस समय समाप्त हो जाती है जब वह \frac{1}{3}(a+2h) ऊंचाई तक पहुंच जाता है।साथ ही यह भी सिद्ध कीजिए कि कण का प्रक्षेप बिन्दु से अधिकतम ऊंचाई \frac{(4 a-h)(a+2 h)^{2}}{27a^{2}} तक सम्पूर्ण गति में पहुंच पाता है।
(A heavy particle hangs by an inextensible string of length a from a fixed point and is then projected horizontally with a velocity \sqrt{2}gh .If \frac{5}{2}a>h>a,prove that the circular motion ceases when the particle has reached the height \frac{1}{3}(a+2h).Prove also that the greatest height ever reached by the particle above the point of projection is \frac{(4 a-h)(a+2 h)^{2}}{27a^{2}}.)
(4.)एक कण किसी स्थिर बिन्दु O से एक डोरी जिसकी लम्बाई a है, लटकाया हुआ है।यदि एक कील O’ पर O के क्षैतिज तल पर O से b(<a) दूरी पर हो तो सिद्ध कीजिए कि कण का इसके निम्नत्तम बिन्दु पर निम्निष्ठ प्रक्षेप वेग \sqrt{g(5a-3b)} होना चाहिए जिससे वह डोरी को ढीले हुए बिना कील का पूरा चक्कर लगा सके।
(A particle is hanging from a fixed point O by means of a light string of length a.There is a small smooth nail at O’ in the same horizontal line with O at a distance b(<a) from O.Show that the minimum velocity with which the particle should be projected from its lowest position in order that make a complete revolution round the nail without the string becoming slack is \sqrt{g(5a-3b)} .)
(5.)एक w भार वाला कण जो कि स्थिर बिन्दु से एक भारहीन अवितान्य डोरी से बंधा है और एक उर्ध्वाधर तल में एक वृत्त में घूम रहा है।जब कण अधिकतम तथा न्यूनतम ऊंचाई पर होता है तो डोरी में खिंचाव क्रमशः mw और nw होता है तो सिद्ध कीजिए कि n=m+6.
(A heavy particle of weight w, attached to a fixed point by a light inextensible string,describes a circle in a vertical plane.The tension of the string has the values mw and nw respectively.When the particle is at the highest and lowest point of its path,show that n=m+6.)

उपर्युक्त उदाहरण के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।

7.कब एक कण एक ऊर्ध्वाधर में बढ़ रहा है ? (When a particle is moving in a vertical ?)-

एक कण ऊर्ध्वाधर तल में एक गोलाकार पथ में घूम रहा है। यह l लंबाई के एक छोर के एक छोर पर जुड़ा हुआ है जिसका दूसरा छोर निश्चित बिन्दु पर है।सबसे निम्नत्तम बिंदु पर वेग u है तब यह उर्ध्वाधर गति करता है। उदाहरणार्थ
जब स्ट्रिंग कोणों में दो स्थिति से गुजरती हैं 30∘ और 60 तब ऊर्ध्वाधर (सबसे कम स्थिति) से क्रमशः T_{1} और T_{2} हैं।

8.एक ऊर्ध्वाधर सर्कल में गति क्या है? (What is motion in a vertical circle?)-

किसी ऊर्ध्वाधर वृत्त में किसी पिंड की गति का अध्ययन करते समय हमें गुरुत्वाकर्षण के प्रभाव पर विचार करना होगा। पृथ्वी के गुरुत्वाकर्षण क्षेत्र के प्रभाव के कारण, शरीर के वेग के परिमाण और स्ट्रिंग में तनाव लगातार बदलते रहते हैं। … इसलिए वर्टिकल सर्कल में गति एक समान वृत्तीय गति नहीं है।

उपर्युक्त के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।

9.क्या लंबवत वृत्ताकार गति में सेंट्रीपीटल बल स्थिर है? (Is centripetal force constant in vertical circular motion?)-

रेडियल (सेंट्रिपेटल) बल स्थिर है (जैसे गुरुत्वाकर्षण के एक स्थिर बल के प्रभाव में पृथ्वी के बारे में घूमने वाला उपग्रह)। गति में परिवर्तन के जवाब में वृत्तीय गति इसकी त्रिज्या को समायोजित करती है।इसका मतलब है कि एक समान वृत्तीय गति के मामले के विपरीत,वृत्तीय पथ का त्रिज्या चर है।

उपर्युक्त के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।

10.जब गेंद सबसे नीचे होती है तो स्ट्रिंग में तनाव क्या होता है? (What is the tension in the string when the ball is at the bottom?)-

जब गेंद सर्कल के नीचे होती है, तो स्ट्रिंग में तनाव 15 N होता है।
वृत्ताकार पथ के तल पर, स्ट्रिंग में तनाव कार्य करता है जबकि गेंद का त्वरण नीचे होता है।अपने गोलाकार पथ में दो बार, स्ट्रिंग पूरी तरह से है।

उपर्युक्त के द्वारा चिकने ऊर्ध्वाधर वृत्त के अंदर गति (Motion inside a smooth vertical circle) समझ सकते हैं।

Also Read This Article:-Simple Harmonic Motion Formula

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here