Equation of Right Circular Cylinder
1.लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder),त्रिविम निर्देशांक ज्यामिति में लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder in 3D):
लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder) में लम्बवृत्तीय बेलन की परिभाषा निम्न है:लम्बवृत्तीय बेलन की परिभाषा (Definition of Right Circular Cylinder):
एक सरल रेखा द्वारा जनित पृष्ठ लम्बवृत्तीय बेलन कहलाता है यदि सरल रेखा एक निश्चित वृत्त को प्रतिच्छेदित करे तथा वृत्त के तल के लम्बवत् हो।निश्चित वृत्त को निर्देशक वृत्त (Guiding Circle) कहते हैं।
इस दशा में जनक रेखाएँ बेलन के अक्ष से नियत दूरी पर होती हैं।इस नियत दूरी को बेलन की त्रिज्या (radius) कहते हैं।
लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder):
इस लम्बवृत्तीय बेलन का समीकरण ज्ञात करना जिसकी त्रिज्या r तथा अक्ष के समीकरण \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} हैं।
(To find the equation of right circular cylinder whose axes is the line \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} and radius is r.)
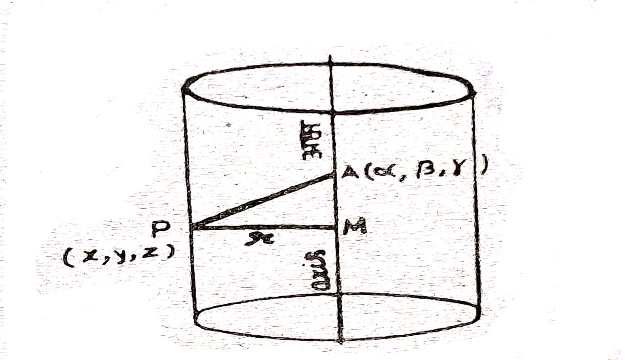
लम्बवृत्तीय बेलन पर कोई बिन्दु P(x,y,z) लो तब सलंग्न चित्रानुसार P(x,y,z) की बेलन के अक्ष से दूरी PM=r होगी।
अब \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} नियत बिन्दु A(\alpha,\beta ,\gamma) से गुजरती है।
A तथा P को मिलाओ तब एक समकोण त्रिभुज होगा।
A P^{2}=PM^{2}+A M^{2} \\ \Rightarrow(x-\alpha)^{2}+(y-\beta)^{2}+(z-\gamma)^{2}= r^{2}+\left[\frac{l(x-\alpha)+m(y-\beta)+n(z-\gamma)}{\sqrt{l^{2}+m^{2}+ n^{2}}}\right]^{2} \\ \Rightarrow\left[(x-\alpha)^{2}+(y-\beta)^{2}+(z-\gamma)^{2}\right]\left(l^{2}+m^{2}+n^{2}\right)-[l(x-\alpha)+m(y-\beta)+n(z-\gamma)]^{2} =r^{2}\left ( l^{2}+m^{2}+n^{2} \right ) \\ \Rightarrow \Sigma[(y-\beta) n-(z-\gamma) m)]^{2}=r^{2}\left(l^{2}+m^{2}+n^{2}\right)
जो कि लम्बवृत्तीय बेलन का अभीष्ट समीकरण है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Equation of Cone with Vertex at Origin
2.लम्बवृत्तीय बेलन का समीकरण के साधित उदाहरण (Equation of Right Circular Cylinder Solved Examples):
उस लम्बवृत्तीय बेलनों के समीकरण ज्ञात कीजिए जिनके अक्ष एवं त्रिज्या निम्नलिखित हैं:
(Find the equations of a right circular cylinders whose axis and radius are are the following):(Example 1 to 5):
Example:1.\frac{x-1}{2}=\frac{y-3}{2}=\frac{z-5}{-1} ; 3
Solution:बेलन के अक्ष की समीकरण: \frac{x-1}{2}=\frac{y-3}{2}=\frac{z-5}{-1}
तथा त्रिज्या (r)=3
माना कि बेलन पर कोई बिन्दु P(x,y,z) है।अब P से PM अक्ष पर लम्ब खींचा।स्पष्टतः अक्ष (1,3,5) से गुजरता है।
अब समकोण \triangle OPM से:
O P^{2}=P M^{2}+O M^{2} \\ (x-1)^{2}+(y-3)^{2}+(z-5)^{2}=(3)^{2}+\left[\frac{2(x-1)+2(y-3)-1(z-5)}{\sqrt{(2)^{2}+(2)^{2}+(-1)^{2}}}\right]^{2} \\ \Rightarrow x^{2}-2 x+(x-1)^{2}+(y-3)^{2}+(z-5)^{2}=9+\frac{(2 x-2+2 y-6-z+5)^{2}}{9} \\ \Rightarrow 9\left[(x-1)^{2}+(y-3)^{2}+(z-5)^{2}\right]-(2 x+2 y+z-3)^{2}=81
जो कि बेलन का अभीष्ट समीकरण है।
Example:2. \frac{x-3}{4}=\frac{y-4}{5}=\frac{z-5}{6} ; 3
Solution:बेलन के अक्ष की समीकरण: \frac{x-3}{4}=\frac{y-4}{5}=\frac{z-5}{6}
तथा त्रिज्या (r)=3
माना कि बेलन पर कोई बिन्दु P(x,y,z) है।अब P से PM अक्ष पर लम्ब खींचा।स्पष्टतः अक्ष (3,4,5) से गुजरता है।
अब समकोण \triangle OPM से:
OP^{2}=PM^{2}+O M^{2}\\ (x-3)^{2}+(y-4)^{2}+(z-5)^{2}=3^{2}+\left[\frac{4(x-3)+5(y-4)+6(z-5)}{\sqrt{(4)^{2}+(5)^{2}+(6)^{2}}}\right]\\ \Rightarrow(x-3)^{2}+(y-4)^{2}+(z-15)^{2}=9+\frac{(4 x-12+5 y-20+6 z-30)^{2}}{77} \\ \Rightarrow x^{2}-6 x+9+y^{2}-8 y+16+z^{2}-10 z+25=\frac{693+(4 x+5 y+6 z-62)^{2}}{77} \\ \Rightarrow 77 x^{2}+77 y^{2}+77 z^{2}-462 x-616 y-770 z+3850=693+(4 x+5 y)^{2}+(6 z-62)^{2}+2(4 x+5 y)(6 z-62) \\ \Rightarrow 77 x^{2}+77 y^{2}+77 z^{2}-462 x-616 y-770 z+3850= 693+16 x^{2}+25 y^{2}+40 x y +36 z^{2}+3844-744 z+48 x z-496 x+60 y z-620 y \\ \Rightarrow 61 x^{2}+52 y^{2}+41 z^{2}-40 x y-48 z x-60 y z+34 x+4 y-26 z-687=0
जो कि बेलन का अभीष्ट समीकरण है।
Example:3. \frac{x-1}{2}=\frac{y-2}{1}=\frac{z-3}{2} ; 2
Solution:बेलन के अक्ष की समीकरण: \frac{x-1}{2}=\frac{y-2}{1}=\frac{z-3}{2}
तथा त्रिज्या (r)=2
माना कि बेलन पर कोई बिन्दु P(x,y,z) है।अब P से PM अक्ष पर लम्ब खींचा।स्पष्टतः अक्ष (1,2,3) से गुजरता है।
अब समकोण \triangle OPM से:
OP^{2}=PM^{2}+OM^{2} \\(x-1)^{2}+(y-2)^{2}+(z-3)^{2}=2^{2}+\left[\frac{2(x-1)+1(y-2)+2(z-3)}{\sqrt{(2)^{2}+(1)^{2}+(2)^{2}}}\right]^{2} \\ \Rightarrow x^{2}-2 x+1+y^{2}-4 y+4+z^{2}-6 z+9=4+\frac{(2 x-2+y-2+2 z-6)^{2}}{9} \\ \Rightarrow 9 x^{2}-18 x+9 y^{2}-36 y+9 z^{2}-54 z+126=36+(2 x+y)^{2}+(2 z-1)^{2}+2(2 x+y)+(2z-10) \\ \Rightarrow 9 x^{2}+9 y^{2}+9 z^{2}-18 x-36 y-54 z+126=36+4 x^{2}+4 x y+y^{2}+4 z^{2}-40 z+100+8 x z-40 x+4 z y-20 y \\ \Rightarrow 5 x^{2}+8 y^{2}+5 z^{2}-4 y z-8 z x-4 x y+22 x-16 y-14 z-10=0
जो कि बेलन का अभीष्ट समीकरण है।
Example:4.\frac{x-1}{2}=\frac{y-2}{-3}=\frac{z-3}{6} ; 2
Solution:बेलन के अक्ष की समीकरण: \frac{x-1}{2}=\frac{y-2}{-3}=\frac{z-3}{6}
तथा त्रिज्या (r)=2
माना कि बेलन पर कोई बिन्दु P(x,y,z) है।अब P से PM अक्ष पर लम्ब खींचा।स्पष्टतः अक्ष (1,2,3) से गुजरता है।
अब समकोण \triangle OPM से:
O P^{2}=PM^{2}+OM^{2} \\ (x-1)^{2}+(y-2)^{2}+(z-3)^{2}=2^{2}+\left[\frac{\left[2(x-1)-3(y-2)+6(z-3)\right]}{\sqrt{(2)^{2}+(-3)^{2}+(6)^{2}}}\right]^{2} \\ \Rightarrow x^{2}-2 x+1+y^{2}-4 y+4+z^{2}-6 z+9=4+\frac{(2 x-2-3 y+6+6 z-18)^{2}}{49} \\ \Rightarrow 49 x^{2}+49 y^{2}+49 z^{2}-98 x-196 y-294 z+686=196+(2 x-3 y+6 z-14)^{2} \\ \Rightarrow 49 x^{2}+49 y^{2}+49 z^{2}-98 x-196 y-294 z+686=196+(2 x-3 y)^{2}+(6 z-14)^{2}+2(2 x-3 y)(6 z-14) \\ \Rightarrow 49 x^{2}+49 y^{2}+49 z^{2}-98 x-196 y-294z+686=196+4 x^{2}+9 y^{2}-12 x y +36 z^{2}+196-168 z+24 x z-56 x-36 y z+84 y \\ \Rightarrow 45 x^{2}+40 y^{2}+13 z^{2}+36 y z-24 z x+12 x y-42 x-280 y-126 z+294=0
जो कि बेलन का अभीष्ट समीकरण है।
Example:5.\frac{x-1}{2}=\frac{y}{3}=\frac{z-3}{1} ; 2
Solution:बेलन के अक्ष की समीकरण: \frac{x-1}{2}=\frac{y}{3}=\frac{z-3}{1}
तथा त्रिज्या (r)=2
माना कि बेलन पर कोई बिन्दु P(x,y,z) है।अब P से PM अक्ष पर लम्ब खींचा।स्पष्टतः अक्ष (1,0,3) से गुजरता है।
अब समकोण \triangle OPM से:
O P^{2}=P M^{2}+O M^{2} \\ (x-1)^{2}+y^{2}+(z-3)^{2}=2^{2}+\left[\frac{2(x-1)+3 y+1(z-3)}{\sqrt{2^{2}+3^{2}+1^{2}}}\right]^{2} \\ \Rightarrow x^{2}-2 x+1+y^{2}+z^{2}-6 z+9=4+\frac{(2 x-2+3 y+z-3)^{2}}{14} \\ \Rightarrow 14 x^{2}+14 y^{2}+14 z^{2}-28 x-84 z+140=56+(2 x+3 y)^{2}+(z-5)^{2}+2(2 x+3 y)(z-5) \\ \Rightarrow 14 x^{2}+14 y^{2}+14 z^{2}-28 x-84 z+140=56+4 x^{2}+9 y^{2}+12 x y+ z^{2}-10 z+25+4 x z-20 x+6 y z-30 y \\ \Rightarrow 10 x^{2}+5 y^{2}+13 z^{2}-12 x y-6 y z-4 z x-8 x+30 y-74 z+59=0
जो कि बेलन का अभीष्ट समीकरण है।
Example:6.किसी लम्बवृत्तीय बेलन की निर्देशक-वक्र x^{2}+y^{2}+z^{2}=9 , x-2 y+2 z=3 है।बेलन का समीकरण ज्ञात कीजिए।
(Find the equation of the right circular cylinder whose guiding circle is x^{2}+y^{2}+ z^{2}=9, x-2 y+2 z=3.)
Solution:गोले के केन्द्र (0,0,0) है तथा तल x-2y+2z=3 पर O से लम्ब ON है।यदि ON=p तब
p=\frac{3}{\sqrt{(1)^{2}+(-2)^{2}+(2)^{2}}}=\frac{3}{\sqrt{9}}=1
वृत्त की त्रिज्या=\sqrt{r^{2}-p^{2}} \\ =\sqrt{9-1}=\sqrt{8}
अब लम्बवृत्तीय बेलन का अक्ष O से होकर जानेवाला तल x-2y+2z=3 का अभिलम्ब है।अतः बेलन का अक्ष के समीकरण होंगे:
\frac{x-0}{1}=\frac{y-0}{-2}=\frac{z-0}{2} \\ \Rightarrow \frac{x}{1}=\frac{y}{-2}=\frac{z}{2}
माना कि बेलन पर कोई बिन्दु P(x,y,z) है।अब P से PM अक्ष पर लम्ब खींचा।तब PM=\sqrt{8},PO को मिलाओ।
अब समकोण \triangle OPM से:
O P^{2}=O M^{2}+MP^{2} \\ \Rightarrow x^{2}+y^{2}+z^{2}=8+[\frac{(x-0)-2(y-0) +2(z-0)}{\sqrt{1^{2}+(-2)^{2}+2^{2}}}]^{2} \\ \Rightarrow x^{2}+y^{2}+z^{2}=8+\frac{(x-2 y+2 z)^{2}}{9} \\ \Rightarrow 9 x^{2}+9 y^{2}+9 z^{2}=72+x^{2}+4 y^{2}+4 z-4 x y-8 y z+4 x z \\ 8 x^{2}+5 y^{2}+5 z^{2}+4 x y+8 y z-4 z x-72=0
जो कि बेलन का अभीष्ट समीकरण है।
उपर्युक्त उदाहरणों के द्वारा लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder),त्रिविम निर्देशांक ज्यामिति में लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder in 3D) को समझ सकते हैं।
3.लम्बवृत्तीय बेलन का समीकरण की समस्याएँ (Equation of Right Circular Cylinder Problems):
(1.)उस लम्बवृत्तीय शंकु का समीकरण ज्ञात करो जिसका अक्ष x=y=z है,शीर्ष मूलबिन्दु है और जिसका अर्द्धशीर्ष कोण 45° है।
(Find the equation of the right circular cone whose axis is x=y=z, vertex is origin and semi-vertical angle is 45°.)
(2.)लम्बवृत्तीय बेलन की समीकरण ज्ञात करो जो वृत्त x^{2}+y^{2}+z^{2}=1 और x+y+z=1 को प्रतिच्छेद करता है।
(Find the equation of the right circular cylinder through the circle of intersection of x^{2}+y^{2}+z^{2}=1 and x+y+z=1.)
उत्तर (Answers): \text { (1.) } x^{2}+y^{2}+z^{2}-4 y z-4 z x-4 x y=0 \\ \text { (2.) } x^{2}+y^{2}+z^{2}-yz-zx-x y=1
उपर्युक्त सवालों को हल करने पर लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder),त्रिविम निर्देशांक ज्यामिति में लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder in 3D) को ठीक से समझ सकते हैं।
Also Read This Article:-How to Find Envelope of a Curve?
4.लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder),त्रिविम निर्देशांक ज्यामिति में लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder in 3D) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.बेलन के अक्ष का समीकरण कैसे ज्ञात करते हैं? (How we find the equation the axis of cylinder?):
Solution:यदि हमें बेलन के अक्ष का समीकरण ज्ञात करना हो तो अक्ष वह रेखा है जो वृत्त के केन्द्र से गुजरती है तथा वृत्त के लम्बवत् है।अब वृत्त का केन्द्र (\frac{a}{2}, \frac{b}{2}, \frac{c}{2}) तथा वृत्त के तल के अभिलम्ब की दिककोज्याएँ (\frac{1}{a}, \frac{1}{b}, \frac{1}{c}) हैं,इसलिए बेलन के अक्ष का समीकरण होगा: \frac{x-(\frac{a}{2})}{\frac{1}{a}}=\frac{y-(\frac{b}{2})}{\frac{1}{b}}=\frac{z-(\frac{c}{2})}{\frac{1}{c}}
प्रश्न:2.z-अक्ष तथा त्रिज्या दी हुई हो तो लम्बवृत्तीय बेलन का समीकरण क्या होगा? (What will be equation of a right circular cylinder of the z-axis and radius are given?):
उत्तर:जब लम्बवृत्तीय बेलन का अक्ष,z-अक्ष है तथा त्रिज्या r है तब लम्बवृत्तीय बेलन का समीकरण x^{2}+y^{2}=r^{2} होगा।
प्रश्न:3.बेलन के अक्ष से गुजरनेवाला बिन्दु तथा दिक्अनुपात व त्रिज्या से बेलन का समीकरण ज्ञात करने का उदाहरण दो। (Given an example of finding the equation of the cylinder by the point passing through the axis of the cylinder and by the direction ratio and radius of the cylinder.):
उत्तर:उस लम्बवृत्तीय बेलन का समीकरण ज्ञात करो जिसका अर्द्धव्यास 3 हो और अक्ष बिन्दु (1,-1,2) से जाता हो और अक्ष के दिक्अनुपात 2,-1,3 हो।
(Find the equation of the right circular cylinder whose radius is 3 and whose axis passes through the point (1,-1,2). The direction ratios of the axis are 2,-1,3.):
Solution:बेलन पर बिन्दु P(x,y,z) है।अब P से PM अक्ष पर लम्ब खींचा।स्पष्टतः अक्ष (1,-1,2) से गुजरता है।अब समकोण \triangle OPM से:
O P^{2}=O M^{2}+MP^{2} \\ (x-1)^{2}+(y+1)^{2}+(z-2)^{2}=3^{2}+ \left[\frac{[2(x-1)-1(y+1)+3(z-2)}{\sqrt{2^{2}+(-1)^{2}+(2)^{2}}}\right]^{2} \\ x^{2}-2 x+1+y^{2}+2 y+1+z^{2}-4 z+4=9+\frac{(2 x-2-y-1+3 z-6)^{2}}{14} \\ \Rightarrow 14 x^{2}+14 y^{2}+14 z^{2}-28 x+28 y-56 z+84=126+4 x^{2}+y^{2}-4 x y+9 z^{2}+81-54 z +12 z x-36 x-6 y z+18 y \\ \Rightarrow 10 x^{2}+13 y^{2}+5 z^{2}+4 x y-12 z x +6 y z+8 x+10 y-2 z-123=0
उपर्युक्त प्रश्नों के उत्तर द्वारा लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder),त्रिविम निर्देशांक ज्यामिति में लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder in 3D) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Equation of Right Circular Cylinder
लम्बवृत्तीय बेलन का समीकरण
(Equation of Right Circular Cylinder)
Equation of Right Circular Cylinder
लम्बवृत्तीय बेलन का समीकरण (Equation of Right Circular Cylinder) में लम्बवृत्तीय बेलन
की परिभाषा निम्न है:लम्बवृत्तीय बेलन की परिभाषा (Definition of Right Circular Cylinder):
एक सरल रेखा द्वारा जनित पृष्ठ लम्बवृत्तीय बेलन कहलाता है