Congruence of Triangles in Class 9th
1.कक्षा 9वीं में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9th),त्रिभुजों की सर्वांगसमता के महत्त्वपूर्ण उदाहरण (Important Illustrations of Congruence of Triangles):
कक्षा 9वीं में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9th) के इस आर्टिकल में सर्वांगसमता पर आधारित सवालों को हल करके त्रिभुजों की सर्वांगसमता तथा उसके आधार पर विशिष्ट सवालों के हल समझेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Parallelogram in Class 9th
2.कक्षा 9वीं में त्रिभुजों की सर्वांगसमता के साधित उदाहरण (Congruence of Triangles in Class 9th Solved Illustrations):
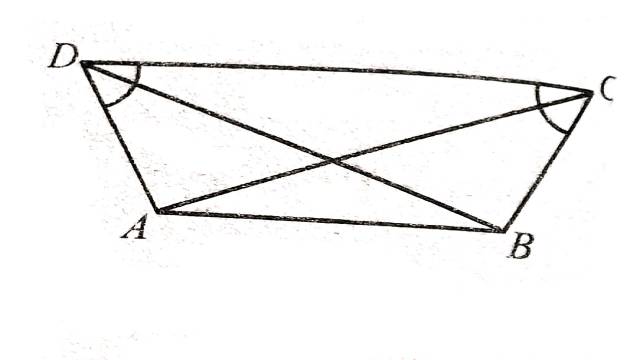
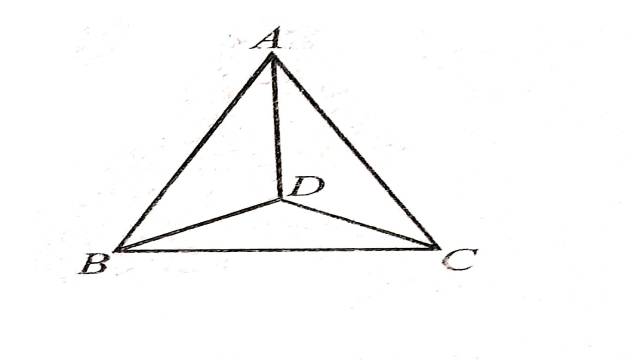
Illustration:1.चित्र में,एक चतुर्भुज ABCD में BC=AD एवं \angle ADC=\angle BCD हो,तो सिद्ध कीजिए:
(i)AC=BD (ii) \angle ACD=\angle CDB
Solution:दिया है (Given):BC=AD एवं \angle ADC=\angle BCD
सिद्ध करना है (To Prove): (i)AC=BD (ii) \angle ACD=\angle CDB
उपपत्ति (Proof): \triangle ADC एवं \triangle BCD में
AD=BC (दिया है)
CD=CD (उभयनिष्ठ भुजा)
\angle ADC=\angle BCD (दिया है)
अतः SAS सर्वांगसमता नियम से
\triangle ADC \cong \triangle BCD
AC=BD एवं \angle ACD=\angle CDB (सर्वांगसम त्रिभुजों के संगत अवयव बराबर होते हैं)
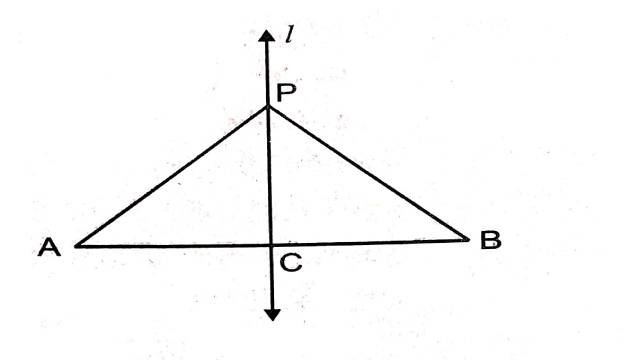
Illustration:2.AB एक रेखाखण्ड है और रेखा l इसका लम्ब समद्विभाजक है।यदि l पर स्थित कोई बिन्दु P है,तो दर्शाइए कि P, बिन्दुओं A और B से समदूरस्थ (equidistant) है।
Solution:दिया है (Given):AB का लम्ब समद्विभाजक l है अतः AC=BC तथा \angle ACP=\angle BCP
सिद्ध करना है (To Prove):AP=BP
उपपत्ति (Proof): \triangle PCA और \triangle PCB में
AC=BC (C,AB का मध्य बिन्दु है)
\angle PCA=\angle PCB=90^{\circ} (दिया है)
PC=PC (उभयनिष्ठ भुजा)
अतः SAS सर्वांगसमता नियम से
\triangle PCA \cong \triangle PCB
PA=PB (सर्वांगसम त्रिभुजों की संगत भुजाएँ बराबर होती हैं)
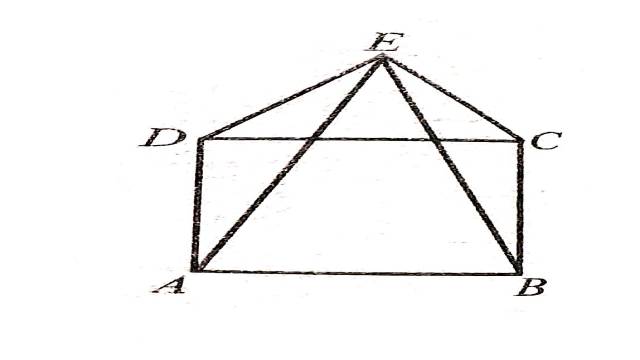
Illustration:3.चित्र के अनुसार ABCD एक वर्ग है तथा \triangle CDE एक समबाहु त्रिभुज हो,तो सिद्ध कीजिए कि AE=BE
Solution:दिया है (Given):ABCD एक वर्ग है एवं \triangle CDE एक समबाहु त्रिभुज है।
सिद्ध करना है (To Prove):AE=BE
उपपत्ति (Proof): \triangle CDE एक समबाहु त्रिभुज है।
अतः CD=DE=CE ….. (1)
\angle DEC=\angle EDC=\angle DCE=60^{\circ} \cdots(2)
एवं ABCD एक वर्ग है अतः
\angle ADC=\angle BCD=90^{\circ}
दोनों पक्षों में \angle EDC जोड़ने पर:
\angle ADC+\angle EDC=\angle BCD+\angle EDC \\ \Rightarrow \angle EDA=\angle BCD+\angle ECD(\because \angle EDC=\angle ECD) \\ \Rightarrow \angle EDA=\angle ECB \ldots(3)
अब \triangle ADE एवं \triangle BCE में
AD=BC (वर्ग की भुजाएँ)
\angle EDA=\angle ECB (सिद्ध किया है)
DE=EC [(1) से]
SAS सर्वांगसमता गुणधर्म से
\triangle ADE \cong \triangle BCE
AE=BE (सर्वांगसम त्रिभुजों की संगत भुजाएँ बराबर होती हैं)
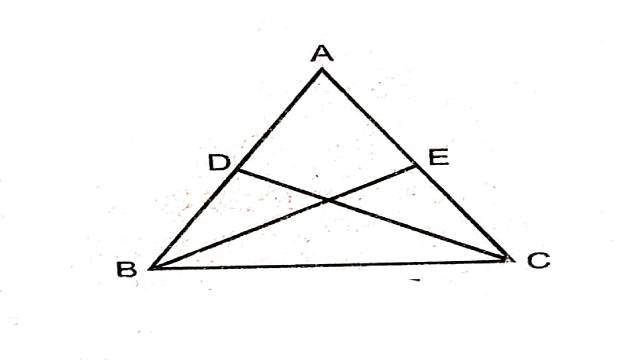
Illustration:4.सिद्ध कीजिए कि समद्विबाहु त्रिभुज की समान भुजाओं को समद्विभाजित करने वाली माध्यिकाएँ समान होती हैं।
Solution:दिया है (Given):एक समद्विबाहु त्रिभुज ABC में समान भुजाओं AB एवं AC के मध्य बिन्दु क्रमशः D एवं E हैं।
सिद्ध करना है (To Prove):BE=CD
उपपत्ति (Proof): \triangle ABC एक समद्विबाहु त्रिभुज है जिसकी भुजाएँ AB और AC समान हैं।
AB=AC ….. (1)
एवं \angle ABC=\angle ACB \cdots(2) (बराबर भुजाओं के अभिमुख कोण)
एवं D एवं E भुजा AB एवं AC के मध्य बिन्दु हैं।
अतः DB=DA=EC=AE … (3)
अब \triangle BCD एवं \triangle BCE में,
BC=BC (उभयनिष्ठ भुजा)
\angle DBC=\angle ECB [(2) से]
BD=CE [(3) से]
SAS सर्वांगसमता गुणधर्म से
\triangle BCD \cong \triangle BCE
BE=CD (सर्वांगसम त्रिभुजों की संगत भुजाएँ बराबर होती हैं)
Illustration:5.चित्र में,AB=AC हैं,एवं \triangle ABC में D एक ऐसा बिन्दु है कि \angle DBC=\angle DCB. सिद्ध कीजिए कि \angle BAC को AD समद्विभाजित करता है।
Solution:दिया है (Given): \triangle ABC में AB=AC एवं \angle DBC=\angle DCB
सिद्ध करना है (To Prove):AD, \angle BAC का समद्विभाजक है।अर्थात् \angle DBC=\angle DCB
उपपत्ति (Proof): \triangle BDC में \angle DBC=\angle DCB
अतः BD=DC (बराबर कोण की सम्मुख भुजाएँ)…. (1)
अब \triangle ABD एवं \triangle ACD में
BD=CD [(1) से]
AD=AD (उभयनिष्ठ भुजा)
AB=AC (दिया है)
SSS सर्वांगसमता गुणधर्म से
\triangle ABD \cong \triangle ACD
\angle BAD=\angle CAD (सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
अतः AD, \angle BAC का समद्विभाजक है।
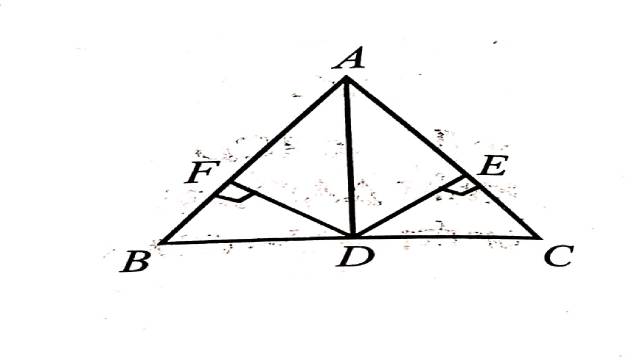
Illustration:6.यदि एक त्रिभुज की एक भुजा के मध्य से दूसरी दो भुजाओं पर डाले गए लम्ब समान हो,तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु होगा।
Solution:दिया है (Given): \triangle ABC की भुजा BC का मध्य बिन्दु D है एवं DE और DF क्रमशः AC एवं AB पर लम्ब हैं एवं DE=DF
सिद्ध करना है (To Prove): \triangle ABC एक समद्विबाहु त्रिभुज है अर्थात् AB=AC
रचना (Constructions):AD को मिलाया।
उपपत्ति (Proof): \triangle BDF एवं \triangle CDE में
कर्ण BD=कर्ण CD (दिया है)
\angle DFB=\angle DEC=90^{\circ}
एवं DF=DE (दिया है)
अर्थात् RHS सर्वांगसमता गुणधर्म से
\triangle BDF \cong \triangle CDE
अतः \angle B=\angle C (सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
AB=AC (बराबर कोण की सम्मुख भुजाएँ बराबर होती है)
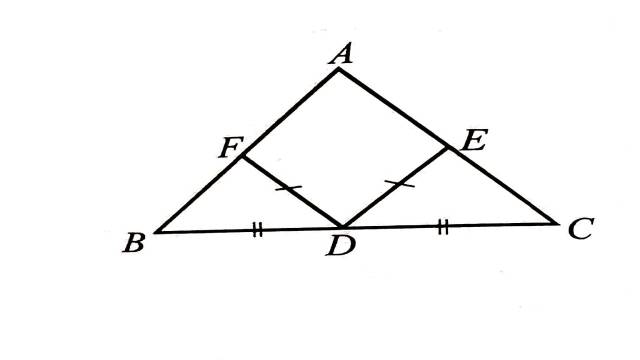
Illustration:7.एक समद्विबाहु त्रिभुज ABC में AB=AC हो,एवं भुजा BC,AC एवं AB के मध्य बिन्दु क्रमशः D,E,F हो,तो सिद्ध कीजिए कि DE=DF
Solution:दिया है (Given):समद्विबाहु \triangle ABC में AB=AC तथा भुजा BC,AC एवं AB के मध्य बिन्दु क्रमशः D,E,F हैं।
सिद्ध करना है (To Prove):DE=DF
उपपत्ति (Proof): \triangle ABC में
AB=AC ….. (1)
\triangle BDF एवं \triangle CDE में
BD=CD (D,भुजा BC का मध्य बिन्दु है)
CE=BF (दिया है कि AB=AC)
एवं \angle B=\angle C (समान भुजाओं के सामने के कोण)
अतः SAS सर्वांगसमता गुणधर्म से
\triangle BDF \cong \triangle CDE
अतः DE=DF (सर्वांगसम त्रिभुजों की संगत भुजाएँ बराबर होती हैं)
Illustration:8.चित्र में,ABC एक समकोण त्रिभुज है,जिसका कोण B समकोण इस प्रकार है कि \angle BCA=2 \angle BAC है।दर्शाइए कि कर्ण AC=2BC है।
Solution:दिया है (Given): \triangle ABC में \angle B=90^{\circ} तथा \angle BCA=2 \angle BAC
सिद्ध करना है (To Prove):AC=2BC
रचना (Construction):CB को बिन्दु D तक इस प्रकार बढाइए कि BC=BD हो तथा AD को मिलाइए।
उपपत्ति (Proof): \triangle ABC और \triangle ABD में
BC=BD (रचना से)
AB=AB (उभयनिष्ठ भुजा)
\angle ABC=\angle ABD=90^{\circ}
SAS सर्वांगसमता गुणधर्म से
\triangle ABC \cong \triangle ABD
अतः \angle CAB=\angle DAB ………(1) (सर्वांगसम त्रिभुजों के संगत अवयव बराबर होते हैं)
और AC=AD ………(2) (सर्वांगसम त्रिभुजों के संगत अवयव बराबर होते हैं)
तथा \angle ACD=\angle ADB ………(3) (सर्वांगसम त्रिभुजों के संगत अवयव बराबर होते हैं)
\angle CAD=\angle CAB+\angle BAD \\ \Rightarrow \angle CAD=\angle CAB+\angle CAB [(1) से]
\Rightarrow \angle CAD=2 \angle CAB \cdots(4)
परन्तु \angle ACB=2 \angle CAB (दिया है)
(3),(4) और (5) से:
\angle CAD=\angle ACD=\angle ADC
अर्थात् \triangle ACD एक समबाहु त्रिभुज है
अतः AC=CD
AC=2BC (क्योंकि BC=BD)
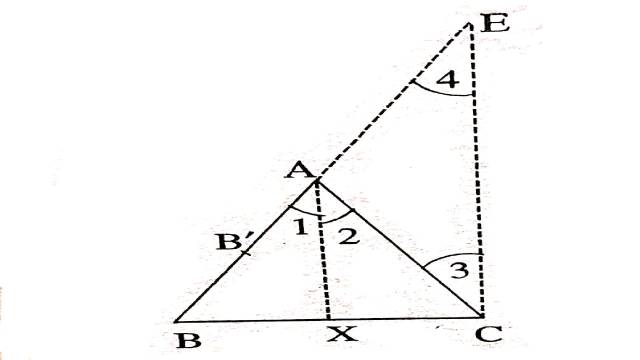
Illustration:9.यदि त्रिभुज के किसी कोण का समद्विभाजक सम्मुख भुजा को भी समद्विभाजित करता है तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु होगा।
Solution:दिया है (Given): \triangle ABC में AX, \angle BAC को समद्विभाजित करता है तथा BX=XC
सिद्ध करना है (To Prove):AB=AC
रचना (Construction):C से AX के समान्तर रेखा CE खींचिए जो BA (बढ़ी हुई) को E पर काटे।
उपपत्ति (Proof): XA \| CE तथा AC तिर्यक रेखा है
\therefore \angle 3 =\angle 2 (एकान्तर कोण)….(1)
तथा \angle 1=\angle 4 (संगत कोण)…..(2)
\because A X, \angle BAC का अर्द्धक है।
\therefore \angle 2=\angle 1 (दिया है)
(1), (2) तथा (3) से:
\angle 3=\angle 4
\triangle AEC के आधार के कोण बराबर हैं अतः
AE=AC ….. (4)
\because \triangle BCE में AX \| CE \\ \therefore \frac{BX}{XC}=\frac{BA}{AE} (आधारभूत आनुपातिक प्रमेय से)
\Rightarrow \frac{BX}{XC}=\frac{BA}{AC} [(4) से]
\Rightarrow \frac{BX}{BX}=\frac{B A}{A C} [BX=XC दिया है]
\therefore AB=AC
अतः \triangle ABC समद्विबाहु त्रिभुज है।
उपर्युक्त उदाहरणों के द्वारा कक्षा 9वीं में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9th),त्रिभुजों की सर्वांगसमता के महत्त्वपूर्ण उदाहरण (Important Illustrations of Congruence of Triangles) को समझ सकते हैं।
3.कक्षा 9वीं में त्रिभुजों की सर्वांगसमता पर आधारित समस्याएँ (Problems Based on Congruence of Triangles in Class 9th):
(1.)यदि किसी त्रिभुज की दो भुजाएँ और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों,तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।क्या यह कथन सत्य है? क्यों?
(2.)यदि किसी त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोण और एक भुजा के बराबर हों,तो त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।क्या यह कथन सत्य है? क्यों?
(3.)दिया हुआ है।क्या यह कथन सत्य है कि BC=QR है? क्यों?
उत्तर (Answers):(1.)नहीं,कोण दोनों भुजाओं के अन्तर्गत होना चाहिए।
(2.)हाँ,दो कोण और एक भुजा समान होने पर दोनों त्रिभुज सर्वांगसम होते हैं।
(3.)नहीं,BC=PQ होना चाहिए।
उपर्युक्त सवालों को हल करने पर कक्षा 9वीं में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9th),त्रिभुजों की सर्वांगसमता के महत्त्वपूर्ण उदाहरण (Important Illustrations of Congruence of Triangles) को ठीक से समझ सकते हैं।
Also Read This Article:- Inequalities in Triangles in Class 9th
4.कक्षा 9वीं में त्रिभुजों की सर्वांगसमता (Frequently Asked Questions Related to Congruence of Triangles in Class 9th),त्रिभुजों की सर्वांगसमता के महत्त्वपूर्ण उदाहरण (Important Illustrations of Congruence of Triangles) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.त्रिभुजों की सर्वांगसमता में नामों के क्रम में क्या सम्बन्ध होता है? (What is the Relation Between the Order of Names in the Congruence of Triangles?):
उत्तर:यदि \triangle ABC , \triangle DEF के सर्वांगसम है और संगतता ABC \longrightarrow EFG से एक त्रिभुज के छः भाग दूसरे त्रिभुज के छः भागों के सर्वांगसम हो जाते हैं,तो हम लिखते हैं:
\triangle ABC \cong \triangle EFG
त्रिभुजों के नामों में अक्षरों का क्रम,उस संगतता का भी संकेत करता है जिससे सर्वांगसमता स्थापित होती है।नाम लिखने के क्रम से,हम आसानी से छः समिकाएँ प्राप्त कर सकते हैं जो दो सर्वांगसम त्रिभुजों के संगत भागों के बीच होती है:
जैसे: \angle A =\angle E , \angle B =\angle F , \angle C =\angle G , AB=EF, BC=FG, AC=EG
प्रश्न:2.दो त्रिभुजों की सर्वांगसमता के लिए पर्याप्त प्रतिबन्ध क्या है? (What is the Sufficient Condition for the Congruence of Two Triangles?):
उत्तर:(1.)SSS सर्वांगसमता गुणधर्म या (2.)SAS सर्वांगसमता गुणधर्म या (3.)ASA सर्वांगसमता गुणधर्म या (4.)RHS सर्वांगसमता गुणधर्म
प्रश्न:3.कोण-कोण-भुजा सर्वांगसमता क्या है? (What is Angle-Angle-Side Congruence?):
उत्तर:दो त्रिभुजों में यदि एक त्रिभुज के दो कोण और एक भुजा (जो कोणों के अंतरित न हो) क्रमशः दूसरे त्रिभुज के संगत दो कोणों और एक भुजा के बराबर हो,तो वे त्रिभुज सर्वांगसम होते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा कक्षा 9वीं में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9th),त्रिभुजों की सर्वांगसमता के महत्त्वपूर्ण उदाहरण (Important Illustrations of Congruence of Triangles) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Congruence of Triangles in Class 9th
कक्षा 9वीं में त्रिभुजों की सर्वांगसमता
(Congruence of Triangles in Class 9th)
Congruence of Triangles in Class 9th
कक्षा 9वीं में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9th) के इस
आर्टिकल में सर्वांगसमता पर आधारित सवालों को हल करके त्रिभुजों की सर्वांगसमता तथा
उसके आधार पर विशिष्ट सवालों के हल समझेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.