cauchy Integral formula
1.कोशी समाकल सूत्र का परिचय (Introduction to cauchy Integral formula):
कोशी समाकल सूत्र (cauchy Integral formula) के द्वारा किसी विश्लेषिक फलन का किसी बिन्दु पर मान,विश्लेषिक फलन के अवकलज का मान किसी बिन्दु पर ज्ञात किया जा सकता है। इसलिए सर्वप्रथम हम कोशी समाकल सूत्र को सिद्ध करेंगे।इसके पश्चात् उदाहरणों के द्वारा कोशी समाकल सूत्र को समझेगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Hooke’s law for elastic string
2.कोशी समाकल सूत्र (cauchy Integral formula)-
(1.)प्रमेय (Theorem)-
माना कि f(z) चापकलनीय जोरदां वक्र C द्वारा परिबद्ध एकश: सम्बद्ध क्षेत्र G में एक विश्लेषिक फलन है तथा C पर यह संतत फलन है तो G के किसी बिन्दु { z }_{ 0 }के लिए
(Let f(z) be an analytic function in a simply connected domain G bounded by a rectfiable Jordan curve C and is continuous on C .Then for any point{ z }_{ 0 } of G.
f\left( { z }_{ 0 } \right) =\frac { 1 }{ 2\pi i } \int _{ c }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } dz
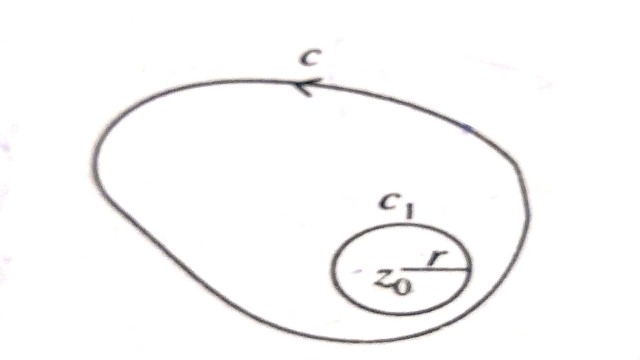
उपपत्ति (Proof):प्रमेय को सिद्ध करने के लिए एक वृत्त { c }_{ 1 }:\left| z-{ z }_{ 0 } \right| =rलीजिए। जहां r इतना छोटा हो ताकि वृत्त{ c }_{ 1 } पूर्णतः C के अन्दर स्थित हो।
माना किg\left( z \right) =\int _{ c }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } यह फलन z={ z }_{ 0 }जहां हर का मान शून्य है,के अलावा C द्वारा परिबद्ध पूरे क्षेत्र में विश्लेषिक फलन होगा। अतः C तथा { c }_{ 1 }द्वारा परिबद्ध द्वि-सम्बद्ध ( doubly connected) क्षेत्र में फलन f(z) विश्लेषिक फलन होगा।
तो कोशी प्रमेय का बहुसम्बन्धित प्रदेश के लिए विस्तार से-
\int _{ c }^{ \quad }{ g(z)dz } =\int _{ { c }_{ 1 } }^{ \quad }{ g(z) } dz\\ \quad \Rightarrow \int _{ c }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } =\int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } dz......(1)
जहां C तथा { c }_{ 1 }दोनों वामावर्त दिशा में लिए हुए है।स्पष्ट है कि कोई दांई ओर का समाकल r से स्वतन्त्र होगा। अतः r को हम जितना चाहे छोटा ले सकते हैं।
\int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } dz=\int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) -f\left( { z }_{ 0 } \right) +f\left( { z }_{ 0 } \right) }{ z-{ z }_{ 0 } } } dz\\ \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } dz=\int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( { z }_{ 0 } \right) }{ z-{ z }_{ 0 } } } dz\quad +\int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) -f\left( { z }_{ 0 } \right) }{ z-{ z }_{ 0 } } } dz
दांई ओर के प्रथम समाकल में z-{ z }_{ 0 }=r\quad { e }^{ i\theta }\quad ,\quad dz=ri\quad { e }^{ i\theta }\quad d\theta लेने पर-
\int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } dz=f\left( { z }_{ 0 } \right) \int _{ 0 }^{ 2\pi }{ \frac { ri\quad { e }^{ i\theta } }{ r\quad { e }^{ i\theta } } } d\theta \quad =\quad 2\pi i\quad f\left( { z }_{ 0 } \right) \\अतः \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } dz=2\pi i\quad f\left( { z }_{ 0 } \right) +\int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) -f\left( { z }_{ 0 } \right) }{ z-{ z }_{ 0 } } } dz.......(2)
चूंकि f(z), C के अन्दर प्रत्येक बिन्दु z={ z }_{ 0 }पर संतत फलन है अतः यह बिन्दु पर भी संतत फलन होगा।
फलत: किसी दिए हुए \varepsilon >0के लिए\delta >0 इस प्रकार विद्यमान होगा कि\left| f\left( z \right) -f\left( { z }_{ 0 } \right) \right| <\varepsilon ........(3)
जबकि\left| z-{ z }_{ 0 } \right| <\delta
चूंकि r का चयन हम इच्छानुसार कर सकते हैं अतः r<\delta लेने पर असमिका (3) के प्रत्येक बिन्दु के लिए सन्तुष्ट होगी।
समीकरण (2) से हम देखते हैं कि
\left| \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) -f\left( { z }_{ 0 } \right) }{ z-{ z }_{ 0 } } } dz \right| \le \int _{ { c }_{ 1 } }^{ \quad }{ \frac { \left| f\left( z \right) -f\left( { z }_{ 0 } \right) \right| }{ \left| z-{ z }_{ 0 } \right| } } \left| dz \right| \\ \quad \quad \quad \quad \quad \quad \quad <\frac { \varepsilon }{ r } \int _{ { c }_{ 1 } }^{ \quad }{ \left| dz \right| } \\ \quad \quad \quad \quad \quad \quad \quad <\frac { \varepsilon }{ r } \left( 2\pi r \right) \\ \quad \quad \quad \quad \quad \quad \quad <2\pi \varepsilon \\ \Rightarrow \left| \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) -f\left( { z }_{ 0 } \right) }{ z-{ z }_{ 0 } } } dz \right| <2\pi \varepsilon ..........(4)
अतः समीकरण (2) तथा (4) से
\left| \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } dz-2\pi i\quad f\left( { z }_{ 0 } \right) \right| <2\pi \varepsilon ..........(5)
चूंकि \varepsilon एक स्वेच्छ संख्या है एवं समीकरण (5) का बायां पक्ष पर निर्भर नहीं करता है। अतः
\int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } dz-2\pi i\quad f\left( { z }_{ 0 } \right) =0\\ अतःf\left( { z }_{ 0 } \right) =\frac { 1 }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } dz..........(6)
समीकरण (1) एवं (6) से कोशी समाकल सूत्र(cauchy Integral formula)
f\left( { z }_{ 0 } \right) =\frac { 1 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ z-{ z }_{ 0 } } } dz
यह कोशी समाकल सूत्र(cauchy Integral formula) है |
3.विश्लेषिक फलन के अवकलज (Derivatives of an analytic function)-
(1.)प्रमेय (Theorem):
यदि एक फलन f(z) सरल संवृत्त कंटूर C के अन्दर एवं ऊपर एक विश्लेषिक फलन हो तो C के अन्दर किसी बिन्दु { z }_{ 0 }पर इसके अवकलज का मान होगा:
(If a function f(z) is analytic within and on a simple closed contour C . Then its derivative at any point{ z }_{ 0 } inside C is given by)
{ f }^{ \prime }\left( { z }_{ 0 } \right) =\frac { 1 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz
उपपत्ति (Proof):माना कि बिन्दु के सामीप्य (neighbourhood) में कोई बिन्दु { z }_{ 0 }+hहै जहां h को हम इच्छानुसार अल्प संख्या का चयन कर सकते हैं तो कोशी समाकल सूत्र से-
f\left( { z }_{ 0 }+h \right) =\frac { 1 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ z-\left( { z }_{ 0 }+h \right) } } dz\\ \frac { f\left( { z }_{ 0 }+h \right) -f\left( { z }_{ 0 } \right) }{ h } =\frac { 1 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \left( \frac { 1 }{ z-{ z }_{ 0 }-h } -\frac { 1 }{ z-{ z }_{ 0 } } \right) f\left( z \right) } dz\\ =\frac { 1 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \left( \frac { 1 }{ z-{ z }_{ 0 }-h } -\frac { 1 }{ z-{ z }_{ 0 } } \right) f\left( z \right) } dz\\ =\frac { 1 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ \left( z-{ z }_{ 0 }-h \right) \left( z-{ z }_{ 0 } \right) } } dz\\ =\frac { 1 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { \left( z-{ z }_{ 0 } \right) f\left( z \right) }{ \left( z-{ z }_{ 0 }-h \right) { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz\\ =\frac { 1 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { \left( z-{ z }_{ 0 }-h+h \right) f\left( z \right) }{ \left( z-{ z }_{ 0 }-h \right) { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz\\ =\frac { 1 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz+\frac { h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ \left( z-{ z }_{ 0 }-h \right) { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz.......(1)
अब एक वृत्त{ c }_{ 1 }:\left| z-{ z }_{ 0 } \right| =r इस प्रकार बनाइए ताकि यह वृत्त पूर्णतः C के अन्दर स्थित हो तो बहुसम्बन्धित प्रदेश के लिए कोशी प्रमेय प्रयोग करने पर हमें प्राप्त होगा
\frac { h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ \left( z-{ z }_{ 0 }-h \right) { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz=\frac { h }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ \left( z-{ z }_{ 0 }-h \right) { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz.........(2)
अब h को इतना छोटा लो ताकि\left| h \right| \le \frac { r }{ 2 } \quad तथा\quad { z }_{ 0 }+h वृत्त C के अन्दर स्थित हो। चूंकि f(z) वक्र{ c }_{ 1 } पर विश्लेषिक फलन है अतः यह परिबद्ध फलन होगा। अतः किसी धनात्मक वास्तविक अचर संख्या M के लिए
\left| f\left( z \right) \right| \le M\quad \quad Z\in G
पुनः\left| \left( z-{ z }_{ 0 }-h \right) \right| \ge \left| z-{ z }_{ 0 } \right| -\left| h \right| \\ \quad \quad \quad \quad \quad \quad \quad \quad \ge r-\frac { r }{ 2 } \\ \quad \quad \quad \quad \quad \quad \quad \quad \ge \frac { r }{ 2 }
अब\left| \frac { h }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ \left( z-{ z }_{ 0 }-h \right) { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz \right| \le \frac { \left| h \right| }{ 2\pi } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { \left| f\left( z \right) \right| }{ \left| \left( z-{ z }_{ 0 }-h \right) \right| \left| { \left( z-{ z }_{ 0 } \right) }^{ 2 } \right| } } \left| dz \right| \\ \le \frac { M\left| h \right| }{ 2\pi { r }^{ 2 }\left( \frac { r }{ 2 } \right) } \int _{ { c }_{ 1 } }^{ \quad }{ \left| dz \right| } \\ \le \frac { M\left| h \right| }{ 2\pi { r }^{ 2 }\left( \frac { r }{ 2 } \right) } \times 2\pi r
अतः\left| \frac { h }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \frac { f\left( z \right) }{ \left( z-{ z }_{ 0 }-h \right) { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz \right| \le \left( \frac { 2M }{ { r }^{ 2 } } \right) \left| h \right| .......(3)
अब समीकरण (2) एवं (3) से-
\left| \frac { h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ \left( z-{ z }_{ 0 }-h \right) { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz \right| \le \left( \frac { 2M }{ { r }^{ 2 } } \right) \left| h \right| .......(4)\\ \\ \left| \frac { f\left( { z }_{ 0 }+h \right) -f\left( { z }_{ 0 } \right) }{ h } -\frac { h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz \right| \le \left( \frac { 2M }{ { r }^{ 2 } } \right) \left| h \right| .......(5)
अब जब h\rightarrow 0तो समीकरण (5) का दायां पक्ष शून्य को प्रवृत्त करेगा और हमें प्राप्त होगा:
\lim _{ h\rightarrow 0 }{ \frac { f\left( { z }_{ 0 }+h \right) -f\left( { z }_{ 0 } \right) }{ h } } =\frac { h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz
फलत: f\left( z \right) { ,z }_{ 0 } पर अवकलनीय फलन है और
{ f }^{ \prime }\left( { z }_{ 0 } \right) =\frac { h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz.......(6)
यह कोशी समाकल सूत्र(cauchy Integral formula) है |
(2.)प्रमेय ( Theorem):
किसी विश्लेषिक फलन का अवकलज स्वयं एक विश्लेषिक फलन होता है।
(The derivative of an analytic function is itself an analytic function.)
उपपत्ति (Proof):माना कि प्रान्त G में एक विश्लेषिक फलन है।यदि G में C कोई संवृत्त कंटूर तथा{ z }_{ 0 } वक्र C के अन्दर कोई बिन्दु हो तो विश्लेषिक अवकलज प्रमेय से
{ f }^{ \prime }\left( { z }_{ 0 } \right) =\frac { h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz.......(1)
माना कि C के अन्दर के{ z }_{ 0 } सामीप्य में कोई बिन्दु { z }_{ 0 }+hहै तो
\frac { { f }^{ \prime }\left( { z }_{ 0 }+h \right) -{ f }^{ \prime }\left( { z }_{ 0 } \right) }{ h } =\frac { h }{ 2\pi ih } \int _{ { c } }^{ \quad }{ \left[ \frac { 1 }{ { \left( z-{ z }_{ 0 }-h \right) }^{ 2 } } -\frac { 1 }{ { \left( z-{ z }_{ 0 } \right) }^{ 2 } } \right] \times f\left( z \right) } dz\\ =\frac { h }{ 2\pi ih } \int _{ { c } }^{ \quad }{ \left[ \frac { { \left( z-{ z }_{ 0 } \right) }^{ 2 }-{ \left( z-{ z }_{ 0 }-h \right) }^{ 2 } }{ { \left( z-{ z }_{ 0 }-h \right) }^{ 2 }{ \left( z-{ z }_{ 0 } \right) }^{ 2 } } \right] \times f\left( z \right) } dz\\ =\frac { 2 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { z-{ z }_{ 0 }-\frac { h }{ 2 } }{ { \left( z-{ z }_{ 0 }-h \right) }^{ 2 }{ \left( z-{ z }_{ 0 } \right) }^{ 2 } } f\left( z \right) } dz\\ =\frac { 2! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { \left[ \left( z-{ z }_{ 0 }-h \right) +h \right] \left[ \left( z-{ z }_{ 0 }-h \right) +\frac { h }{ 2 } \right] }{ { { \left( z-{ z }_{ 0 } \right) }^{ 3 }\left( z-{ z }_{ 0 }-h \right) }^{ 2 } } f\left( z \right) } dz\\ =\frac { 2! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { { \left( z-{ z }_{ 0 }-h \right) }^{ 2 }+\left( \frac { 3h }{ 2 } \right) \left( z-{ z }_{ 0 }-h \right) +\left( \frac { { h }^{ 2 } }{ 2 } \right) }{ { { \left( z-{ z }_{ 0 } \right) }^{ 3 }\left( z-{ z }_{ 0 }-h \right) }^{ 2 } } f\left( z \right) } dz\\ =\frac { 2! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ { \left( z-{ z }_{ 0 } \right) }^{ 3 } } dz } +\frac { 2!h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { \left( \frac { 3 }{ 2 } \right) \left( z-{ z }_{ 0 } \right) -h }{ { { \left( z-{ z }_{ 0 } \right) }^{ 3 }\left( z-{ z }_{ 0 }-h \right) }^{ 2 } } } f\left( z \right) dz\\ \\ \frac { { f }^{ \prime }\left( { z }_{ 0 }+h \right) -{ f }^{ \prime }\left( { z }_{ 0 } \right) }{ h } -\frac { 2! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ { \left( z-{ z }_{ 0 } \right) }^{ 3 } } dz } =\frac { 2!h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { \left( \frac { 3 }{ 2 } \right) \left( z-{ z }_{ 0 } \right) -h }{ { { \left( z-{ z }_{ 0 } \right) }^{ 3 }\left( z-{ z }_{ 0 }-h \right) }^{ 2 } } } f\left( z \right) dz........(2)
अब हम सिद्ध करेंगे कि यदि h\rightarrow 0तो समीकरण (2) का दायां पक्ष शून्य की ओर प्रवृत्त होगा।इसके लिए एक वृत्त { c }_{ 1 }:\left| z-{ z }_{ 0 } \right| =rवक्र C के अन्दर खींचो तो बहुसम्बन्धित प्रदेश के लिए कोशी प्रमेय से
\frac { 2!h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { \left( \frac { 3 }{ 2 } \right) \left( z-{ z }_{ 0 } \right) -h }{ { { \left( z-{ z }_{ 0 } \right) }^{ 3 }\left( z-{ z }_{ 0 }-h \right) }^{ 2 } } } f\left( z \right) dz=\frac { 2!h }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { \left( \frac { 3 }{ 2 } \right) \left( z-{ z }_{ 0 } \right) -h }{ { { \left( z-{ z }_{ 0 } \right) }^{ 3 }\left( z-{ z }_{ 0 }-h \right) }^{ 2 } } } f\left( z \right) dz.......(3)
h का इस प्रकार चयन करो ताकि\left| h \right| \le \frac { r }{ 2 } \quadतथा \quad { z }_{ 0 }+h वृत्त { c }_{ 1 }में ही रहे।
अब\left| z-{ z }_{ 0 }-h \right| \ge \left| z-{ z }_{ 0 } \right| -\left| h \right| \ge \left( \frac { r }{ 2 } \right) \\और\quad\left| \frac { 3 }{ 2 } \left( z-{ z }_{ 0 } \right) -h \right| \le \frac { 3 }{ 2 } \left| z-{ z }_{ 0 } \right| +\left| h \right| \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \le \frac { 3 }{ 2 } r+\left( \frac { r }{ 2 } \right) \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \le 2r\\ पुनः\quad\left| f\left( z \right) \right| \le M\quad \quad Z\in G
अतः समीकरण (3) से-
\left| \frac { 2!h }{ 2\pi i } \int _{ { { c }_{ 1 } } }^{ \quad }{ \frac { \left( \frac { 3 }{ 2 } \right) \left( z-{ z }_{ 0 } \right) -h }{ { { \left( z-{ z }_{ 0 } \right) }^{ 3 }\left( z-{ z }_{ 0 }-h \right) }^{ 2 } } } f\left( z \right) dz \right| =\left| \frac { 2!h }{ 2\pi i } \int _{ { { c }_{ 1 } } }^{ \quad }{ \frac { \left( \frac { 3 }{ 2 } \right) \left( z-{ z }_{ 0 } \right) -h }{ { { \left( z-{ z }_{ 0 } \right) }^{ 3 }\left( z-{ z }_{ 0 }-h \right) }^{ 2 } } } f\left( z \right) dz \right| \\ \le \frac { \left| h \right| }{ \pi } \int _{ { { c }_{ 1 } } }^{ \quad }{ \frac { \left| \left( \frac { 3 }{ 2 } \right) \left( z-{ z }_{ 0 } \right) -h \right| }{ { \left| { z-{ z }_{ 0 }-h } \right| }^{ 2 }{ \left| z-{ z }_{ 0 } \right| }^{ 3 } } } \left| f\left( z \right) \right| \left| dz \right| \\ \le \frac { \left| h \right| 2rM }{ \pi { \left( \frac { r }{ 2 } \right) }^{ 2 }{ r }^{ 3 } } \int _{ { { c }_{ 1 } } }^{ \quad }{ \left| dz \right| } \\ \le \frac { \left| h \right| 2rM }{ \pi { \left( \frac { r }{ 2 } \right) }^{ 2 }{ r }^{ 3 } } \times 2\pi r\\ \le \frac { 16M }{ { r }^{ 3 } } \left| h \right|
स्पष्ट है कि यदि h\rightarrow 0तो दायां पक्ष शून्य की ओर प्रवृत्त होगा।
अतः समीकरण (2) से-
\lim _{ h\rightarrow 0 }{ \frac { { f }^{ \prime }\left( { z }_{ 0 }+h \right) -{ f }^{ \prime }\left( { z }_{ 0 } \right) }{ h } } =\frac { 2! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ 3 } } } \\ { f }^{ \prime \prime }\left( { z }_{ 0 } \right) =\frac { 2! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ 3 } } }
अतः { f }^{ \prime }\left( { z }_{ 0 } \right) का प्रान्त G के किसी बिन्दु\quad z={ z }_{ 0 }
पर अद्वितीय अवकलज{ f }^{ \prime \prime }\left( { z }_{ 0 } \right)
है फलत: { f }^{ \prime }\left( { z } \right) विश्लेषिक फलन होगा।
अतः किसी विश्लेषिक फलन का अवकलज विश्लेषिक फलन होता है।
यह कोशी समाकल सूत्र(cauchy Integral formula) है |
(3.) प्रमेय (Theorem)-
यदि एकश: सम्बद्ध क्षेत्र G में f(z) एक विश्लेषिक फलन तथा G में C एक सरल संवृत्त कंटूर हो तो C के अन्दर प्रत्येक बिन्दु { z }_{ 0 } पर f(z) के प्रत्येक कोटि का अवकलज विद्यमान होगा तथा
(If f(z) is analytic in a simply connected domain G containing a simple closed contour C,then f(z) has derivatives of all orders at each point{ z }_{ 0 } inside C with.)
{ f }^{ n }\left( { z }_{ 0 } \right) =\frac { n! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ n+1 } } } ......(1)
उपपत्ति (Proof):इस प्रमेय को गणितीय आगमन सिद्धान्त से सिद्ध करेंगे।
हम जानते हैं कि{ f }^{ \prime }\left( { z }_{ 0 } \right) =\frac { 1 }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ { \left( z-{ z }_{ 0 } \right) }^{ 2 } } } dz.....(2)
माना कि समीकरण (1) n=m ( एक स्थिर धनात्मक पूर्णांक) के लिए सत्य है। अर्थात्
{ f }^{ m }\left( { z }_{ 0 } \right) =\frac { m! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ m+1 } } } ......(3)\\ { { f }^{ \prime }\left( { z }_{ 0 }+h \right) -{ f }^{ \prime }\left( { z }_{ 0 } \right) }{ h }=\frac { m! }{ 2\pi ih } \int _{ { c } }^{ \quad }{ \left[ \frac { { \left( z-{ z }_{ 0 } \right) }^{ m+1 }-{ \left( z-{ z }_{ 0 }-h \right) }^{ m+1 } }{ { \left( z-{ z }_{ 0 }-h \right) }^{ m+1 }{ \left( z-{ z }_{ 0 } \right) }^{ m+1 } } \right] f\left( z \right) } dz
[जहां C के अन्दर{ z }_{ 0 } के सामीप्य में बिन्दु{ z }_{ 0 }+h है]
=\frac { m! }{ 2\pi ih } \int _{ { c } }^{ \quad }{ \left[ \frac { { \left\{ \left( z-{ z }_{ 0 }-h \right) +h \right\} }^{ m+1 }-{ \left( z-{ z }_{ 0 }-h \right) }^{ m+1 } }{ { \left( z-{ z }_{ 0 }-h \right) }^{ m+1 }{ \left( z-{ z }_{ 0 } \right) }^{ m+1 } } \right] f\left( z \right) } dz\\ =\frac { m! }{ 2\pi ih } \int _{ { c } }^{ \quad }{ \left[ \frac { { { \left( z-{ z }_{ 0 }-h \right) }^{ m+1 }+\left( m+1 \right) h{ \left( z-{ z }_{ 0 }-h \right) }^{ m }+......+ }{ h }^{ m+1 }-{ \left( z-{ z }_{ 0 }-h \right) }^{ m+1 } }{ { \left( z-{ z }_{ 0 }-h \right) }^{ m+1 }{ \left( z-{ z }_{ 0 } \right) }^{ m+1 } } \right] f\left( z \right) } dz\\ =\frac { m! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \left[ { { \left( z-{ z }_{ 0 }-h \right) }^{ m }+\frac { m }{ 2! } { \left( z-{ z }_{ 0 }-h \right) }^{ m-1 }h+......+ }\frac { { h }^{ m } }{ m+1 } \right] \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 }-h \right) }^{ m+1 }{ \left( z-{ z }_{ 0 } \right) }^{ m+1 } } } \\ =\frac { \left( m+1 \right) ! }{ 2\pi i } \left[ \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) \left( z-{ z }_{ 0 }-h+h \right) }{ \left( z-{ z }_{ 0 }-h \right) { \left( z-{ z }_{ 0 } \right) }^{ m+2 } } dz } \right] +\\ \frac { \left( m+1 \right) ! }{ 2\pi i } \left[ \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) }{ { \left( z-{ z }_{ 0 }-h \right) }^{ m+1 }{ \left( z-{ z }_{ 0 } \right) }^{ m+1 } } \left\{ \frac { m }{ 2! } { \left( z-{ z }_{ 0 }-h \right) }^{ m-1 }h+....+\frac { { h }^{ m+1 } }{ m+1 } \right\} dz } \right] \\ =\frac { \left( m+1 \right) ! }{ 2\pi i } \left[ \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ m+2 } } } \right] +\\ \frac { \left( m+1 \right) ! }{ 2\pi i } \left[ h\int _{ { c } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 }-h \right) \left( z-{ z }_{ 0 } \right) }^{ m+2 } } } +h\int _{ { c } }^{ \quad }{ \frac { f\left( z \right) g\left( z \right) dz }{ { \left( z-{ z }_{ 0 }-h \right) }^{ m+1 }{ \left( z-{ z }_{ 0 } \right) }^{ m+1 } } } \right]
जहांg\left( z \right) =\frac { m }{ 2! } { \left( z-{ z }_{ 0 }-h \right) }^{ m-1 }+............+\frac { { h }^{ m-1 } }{ m+1 } .......(4)\\I=\frac { { f }^{ m }\left( { z }_{ 0 }+h \right) -{ f }^{ m }\left( { z }_{ 0 } \right) }{ h } -\frac { \left( m+1 \right) ! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ m+2 } } } \\ =\frac { \left( m+1 \right) !h }{ 2\pi i } \int _{ c }^{ \quad }{ \left[ \frac { 1 }{ z-{ z }_{ 0 } } +\frac { g\left( z \right) }{ { \left( z-{ z }_{ 0 }-h \right) }^{ m } } \right] } \times \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ m+1 }\left( z-{ z }_{ 0 }-h \right) } \\ =\frac { \left( m+1 \right) !h }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \left[ \frac { 1 }{ z-{ z }_{ 0 } } +\frac { g\left( z \right) }{ { \left( z-{ z }_{ 0 }-h \right) }^{ m } } \right] } \times \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ m+1 }\left( z-{ z }_{ 0 }-h \right) } .......(5)
जहां C में एक छोटा वृत्त है।
\left| I \right| \le \frac { \left( m+1 \right) !\left| h \right| }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \left[ \frac { 1 }{ \left| z-{ z }_{ 0 } \right| } +\frac { \left| g\left( z \right) \right| }{ { { \left| z-{ z }_{ 0 }-h \right| }^{ m } } } \right] } \times \frac { \left| f\left( z \right) \right| \left| dz \right| }{ { \left| z-{ z }_{ 0 } \right| }^{ m+1 }\left| z-{ z }_{ 0 }-h \right| } .......(6)
अब, \left| z-{ z }_{ 0 } \right| =r,\left| z-{ z }_{ 0 }-h \right| \ge \frac { r }{ 2 },जहां \left| h \right| \le \frac { r }{ 2 }
पुनः f(z) विश्लेषिक फलन है तथा g(z) जो कि (4) से परिभाषित है एक बहुपद फलन है अतः यह भी विश्लेषिक फलन होगा।फलत: f(z) तथा g(z) दोनों परिबद्ध फलन है।यदि f(z) तथा g(z) के ऊपरी परिबन्ध क्रमशः M तथा N हों तो
\left| f\left( z \right) \right| \le Mऔर\left| g\left( z \right) \right| \le N\quad Z\in G
अब (6) से
\left| I \right| \le \frac { \left( m+1 \right) !\left| h \right| }{ 2\pi i } \int _{ { c }_{ 1 } }^{ \quad }{ \left[ \frac { 1 }{ r } +\frac { N }{ { { \left( \frac { r }{ 2 } \right) }^{ m } } } \right] } \times \frac { M }{ \left( \frac { r }{ 2 } \right) { \left( r \right) }^{ m+1 } } 2\pi r
यदि \left| h \right| \rightarrow 0\quadतो\quad I\rightarrow 0
अतः{ f }^{ m+1 }\left( { z }_{ 0 } \right) =\lim _{ h\rightarrow 0 }{ \frac { { f }^{ m }\left( { z }_{ 0 }+h \right) -{ f }^{ m }\left( { z }_{ 0 } \right) }{ h } } \\ =\frac { \left( m+1 \right) ! }{ 2\pi r } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ m+2 } } }
इससे यह सिद्ध हो गया कि परिणाम (1) n=m+1 के लिए भी सत्य है।फलत: प्रत्येक धनात्मक पूर्णांक मानों n के लिए प्रमेय सत्य होगी।
यह कोशी समाकल सूत्र(cauchy Integral formula) है |
Question-1.कोशी समाकल सूत्र (cauchy Integral formula)से सिद्ध करो कि
(Using Cauchy integral formula,prove that)
\int _{ \left| z \right| =2 }^{ \quad }{ \frac { z-3cosz }{ { \left( Z-\frac { \pi }{ 2 } \right) }^{ 2 } } dz } =8\pi
Solution-\int _{ \left| z \right| =2 }^{ \quad }{ \frac { z-3cosz }{ { \left( Z-\frac { \pi }{ 2 } \right) }^{ 2 } } dz } =8\pi
कोशी समाकल सूत्र से (By cauchy Integral formula)-
{ f }^{ n }\left( { z }_{ 0 } \right) =\frac { n! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ n+1 } } } ......(2)
(1) व (2) की तुलना करने पर-
f\left( z \right) =z-3cosz\\ n+1=2\\ n=1\\ { z }_{ 0 }=\frac { \pi }{ 2 }
उपर्युक्त मान (2) में मान रखने पर
{ f }^{ \prime }\left( \frac { \pi }{ 2 } \right) =\frac { n! }{ 2\pi i } \int _{ \left| z \right| =2 }^{ \quad }{ \frac { z-3cosz }{ { \left( Z-\frac { \pi }{ 2 } \right) }^{ 2 } } dz } \\ f\left( z \right) =z-3cosz\\ { f }^{ \prime }\left( z \right) =1+3sinz\\ { f }^{ \prime }\left( \frac { \pi }{ 2 } \right) =1+3sin\left( \frac { \pi }{ 2 } \right) \\ { f }^{ \prime }\left( \frac { \pi }{ 2 } \right) =1+3\left( 1 \right) =4
समीकरण (3) में मान रखने पर-
2\pi i\left( 4 \right) =\int _{ \left| z \right| =2 }^{ \quad }{ \frac { z-3cosz }{ { \left( Z-\frac { \pi }{ 2 } \right) }^{ 2 } } dz } \\ \int _{ \left| z \right| =2 }^{ \quad }{ \frac { z-3cosz }{ { \left( Z-\frac { \pi }{ 2 } \right) }^{ 2 } } dz } =8\pi i
इस उदाहरण से कोशी समाकल सूत्र ( cauchy Integral formula) को समझा जा सकता है।
Question-2.कोशी समाकल सूत्र(cauchy Integral formula) से मान ज्ञात करो
(Using Cauchy integral formula, Evaluate)
\int _{ c }^{ \quad }{ \frac { sin\pi { z }^{ 2 }+cos\pi { z }^{ 2 } }{ { \left( z-2i \right) }^{ 2 } } dz }
Solution-\int _{ c }^{ \quad }{ \frac { sin\pi { z }^{ 2 }+cos\pi { z }^{ 2 } }{ { \left( z-2i \right) }^{ 2 } } dz }.............(1)
कोशी समाकल सूत्र से (By cauchy Integral formula)-
{ f }^{ n }\left( { z }_{ 0 } \right) =\frac { n! }{ 2\pi i } \int _{ { c } }^{ \quad }{ \frac { f\left( z \right) dz }{ { \left( z-{ z }_{ 0 } \right) }^{ n+1 } } } ......(2)
(1) व (2) की तुलना करने पर
n+1=2\\ n=1\\ { z }_{ 0 }=2i\\ f\left( z \right) =sin\pi { z }^{ 2 }+cos\pi { z }^{ 2 }
उपर्युक्त मान (2) में मान रखने पर
{ f }^{ \prime }\left( 2i \right) =\frac { ! }{ 2\pi i } \int _{ c }^{ \quad }{ \frac { sin\pi { z }^{ 2 }+cos\pi { z }^{ 2 } }{ { \left( z-2i \right) }^{ 2 } } dz } \\ 2\pi i\quad \times \quad { f }^{ \prime }\left( 2i \right) =\int _{ c }^{ \quad }{ \frac { sin\pi { z }^{ 2 }+cos\pi { z }^{ 2 } }{ { \left( z-2i \right) }^{ 2 } } dz } ......(3)\\ f\left( z \right) =sin\pi { z }^{ 2 }+cos\pi { z }^{ 2 }\\ { f }^{ \prime }\left( z \right) =2\pi z\quad cos\pi { z }^{ 2 }-2\pi z\quad sin\pi { z }^{ 2 }\\ { f }^{ \prime }\left( z \right) =2\pi \left( 2i \right) \quad cos\left\{ \pi { \left( 2i \right) }^{ 2 } \right\} -2\pi \left( 2i \right) \quad sin\left\{ \pi { \left( 2i \right) }^{ 2 } \right\} \\ { f }^{ \prime }\left( 2i \right) =4\pi i\quad cos4\pi -\quad 4\pi i\quad sin4\pi \\ { f }^{ \prime }\left( 2i \right) =4\pi i\left( 1 \right) -\quad 4\pi i\left( 0 \right) \\ { f }^{ \prime }\left( 2i \right) =4\pi i.........(4)
समीकरण (3) में मान रखने पर-
2\pi i\left( 4\pi i \right) =\int _{ c }^{ \quad }{ \frac { sin\pi { z }^{ 2 }+cos\pi { z }^{ 2 } }{ { \left( z-2i \right) }^{ 2 } } dz } \\ 8\pi i^{ 2 }=\int _{ c }^{ \quad }{ \frac { sin\pi { z }^{ 2 }+cos\pi { z }^{ 2 } }{ { \left( z-2i \right) }^{ 2 } } dz } \\ \int _{ c }^{ \quad }{ \frac { sin\pi { z }^{ 2 }+cos\pi { z }^{ 2 } }{ { \left( z-2i \right) }^{ 2 } } dz } =-8{ \pi }^{ 2 }
उपर्युक्त उदाहरणों से कोशी समाकल सूत्र ( cauchy Integral formula) को समझा जा सकता है। दोनों उदाहरण कोशी समाकल सूत्र (cauchy Integral formula) पर आधारित है।
Also Read This Article:-Milne Thomson Construction Method
उपर्युक्त विवरण में कोशी समाकल सूत्र ( cauchy Integral formula) के बारे में बताया गया है।
cauchy Integral formula
कोशी समाकल सूत्र ( cauchy Integral formula)
cauchy Integral formula
कोशी समाकल सूत्र (cauchy Integral formula) के द्वारा किसी विश्लेषिक फलन का किसी बिन्दु पर मान,विश्लेषिक फलन के अवकलज का मान किसी बिन्दु पर ज्ञात किया जा सकता है। इसलिए सर्वप्रथम हम कोशी समाकल सूत्र को सिद्ध करेंगे।इसके पश्चात् उदाहरणों के द्वारा कोशी समाकल सूत्र को समझेगे।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |