Relative Velocity and Acceleration
1.आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration),गति विज्ञान में आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration in Dynamics):
आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration) के इस आर्टिकल में आपेक्षिक वेग और त्वरण से सम्बन्धित सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Relative Velocity in Dynamics
2.आपेक्षिक वेग और त्वरण के साधित उदाहरण (Relative Velocity and Acceleration Solved Illustrations):
Illustration:1.एक जहाज,धारा के सापेक्ष जो कि 6 km p.h. के वेग से दक्षिण दिशा में बह रही है,15 km p.h. के वेग से पश्चिम दिशा में जा रहा है।यदि एक रेलगाड़ी उत्तर की ओर 30 km p.h. के वेग से जा रही है तो उसका वेग जहाज के सापेक्ष ज्ञात कीजिए।
(A ship steams due west at the rate of 15 km p.h. relative to the current which is flowing at the rate of 6 km p.h. due south.What is the velocity relative to the ship of a train going due north at the rate of 30 km p.h.)
Solution:जहाज का धारा के सापेक्ष वेग=जहाज का वास्तविक वेग (विपरीत दिशा में)+धारा का वास्तविक वेग
\Rightarrow 15=जहाज का वास्तविक वेग+6
\Rightarrow जहाज का वास्तविक वेग=15-6=9
रेलगाड़ी का जहाज के सापेक्ष आपेक्षिक वेग=15-6=9
रेलगाड़ी का जहाज के सापेक्ष आपेक्षिक वेग=30+9=39 km p.h.
कोण \cos \theta=\frac{\text { आधार }}{\text { कर्ण }}=\frac{15}{39} \\ \Rightarrow \theta=\cos ^{-1}\left(\frac{5}{13}\right)
Illustration:9.दो सीधी रेल लाइनें समपार पर कोण पर अभिसृत होती हैं तथा दो रेलगाड़ियाँ समपार की ओर u तथा v वेगों से रेल लाइनों के जोड़ की ओर चल रही है।यदि रेलों की समपार से प्रारम्भिक दूरियाँ a तथा b है,तो सिद्ध करो कि उनकी परस्पर निकटतम दूरी निम्न होगीः
(Two straight railway coverage to a level crossing at an angle and two trains are moving towards the crossing with velocities u and v.If a and b are initial distances of the trains from the crossing,show that their least distance apart will be):
\frac{(a v-b u) \sin \alpha}{\sqrt{\left(u^2+v^2-2 u v \cdot \cos \alpha\right)}}
Solution:दो रेलगाड़ियों द्वारा t समय में तय की गई दूरियाँ ut और vt है ताकि क्रासिंग से उनकी दूरियाँ a-ut और b-vt और उनकी स्थितियाँ A’ व B’ हैं,तब
\left(A^{\prime} B^{\prime}\right)^2 ={O A^{\prime}}^2+{O B^{\prime}}^2-2 O A^{\prime} \cdot O B^{\prime} \cos \alpha \\ =(a-u t)^2+(b-v t)^2-2(a-u t)(b-v t) \cos \alpha \\ \Rightarrow \left(A^{\prime} B^{\prime}\right)^2 =t^2\left(u^2+v^2-2 u v \cos \alpha\right)-2t(a u+b v-a v \cos \alpha-b u \cos \alpha)+\left(a^2+b^2-2 a b \cos \alpha\right) \cdots(1)
A’B’ निम्नतम होगा यदि
\frac{d}{d t}\left(A^{\prime} B^{\prime}\right)^2=0\\ \Rightarrow 2 t\left(u^2+v^2-2 u v \cos \alpha\right)-2[a(u-v \cos \alpha) +b(v-u \cos \alpha)]=0 \\ \therefore t=\frac{2\left[a(u-v \cos \alpha)+b(v-u \cos \alpha) \right]}{2\left(u^2+v^2-2 u v \cos \alpha\right)} \\ \Rightarrow t=\frac{[a(u-v \cos \alpha)+b(v-u \cos \alpha)]}{\left(u^2+v^2-2 u v \cos \alpha\right)}
t का मान समीकरण (1) में रखने पर:
\left(A^{\prime} B^{\prime}\right)^2=\frac{[a(u-v \cos \alpha)+b(v-u \cos \alpha)]^2}{\left(u^2+ v^2-2 u v \cos \alpha\right)^2} \times \left(u^2+v^2-2 u v \cos \alpha\right)-\frac{2[a(u-v \cos \alpha)+ b(v-u \cos \alpha)} {\left(u^2+v^2-2 u v \cos \alpha\right)} \times (a u+b v-a v \cos \alpha-b u \cos \alpha)+\left(a^2+b^2-2 a b \cos \alpha\right) \\ =\frac{[a(u-v \cos \alpha)+b(v-u \cos \alpha)]^2}{\left(u^2+v^2-2 u v \cos \alpha\right)} -\frac{2[a(u-v \cos \alpha)+b(v-u \cos \alpha)]^2}{\left(u^2+v^2-2 u v \cos \alpha\right)}+\left(a^2+b^2-2 a b \cos \alpha\right) \\ =-\frac{[a(u-v \cos \alpha)+b(v-u \cos \alpha)]^2}{\left(u^2+v^2-2 u v \cos \alpha\right)}+\left(a^2+b^2-2 a b \cos \alpha \right)\\ =\frac{\begin{array}{c} -a^2 u^2-a^2 v^2 \cdot \cos ^2 \alpha-b^2 v^2-b^2 \cdot u^2\cos ^2 \alpha \\ +2 a^2 u v \cos \alpha-2 a b u v+2 a b u^2 \cos \alpha+2 a b v^2 \cos \alpha \\ -2 a \sin v \cos ^2 \alpha+2 b^2 u v \cos \alpha +a^2 u^2 \\ +a^2 v^2-2 u v a^2 \cos \alpha +b^2 u^2+b^2 v^2-2 u v b^2 \cos \alpha \\ -2 u^2 a b \cos \alpha-2 a b v^2 \cos \alpha+4a b u v \cos ^2 \alpha \end{array} }{\left(u^2+v^2-2 u v \cos \alpha\right)} \\ =\frac{a^2 v^2\left(1-\cos ^2 \alpha\right)+b^2 u^2\left(1-\cos ^2 \alpha\right)-2 a b u v\left(1-\cos ^2 \alpha\right) }{\left(u^2+v^2-2 u v \cos \alpha\right)} \\=\frac{a^2 v^2 \sin ^2 \alpha+b^2 u^2 \sin ^2 \alpha-2 a b u v \sin ^2 \alpha}{\left(u^2+v^2-2 u v \cos \alpha\right.} \\ =\frac{\left(a^2 v^2+b^2 u^2-2 a b u v\right) \sin ^2 \alpha}{\left(u^2+v^2-2 u v \cos \alpha\right)} \\ \Rightarrow\left(A^{\prime} B^{\prime}\right)^2=\frac{(a v-b u)^2 \sin ^2 \alpha}{\left(u^2+v^2-2 u v \cos \alpha\right)} \\ \Rightarrow A^{\prime} B^{\prime}=\frac{(a v-b u) \sin \alpha}{\sqrt{u^2+v^2-2 u v \cos \alpha}}
Illustration:10.दो बिन्दुओं P तथा Q को मिलाने वाली रेखा की लम्बाई a अचर है तथा P और Q के वेग की दिशाएं PQ के साथ क्रमशः \alpha व \beta कोण बनाती हैं।सिद्ध करो कि PQ का कोणीय वेग \frac{u \sin (\alpha-\beta)}{a \cos \beta} है,जहाँ u,P का वेग है।
(The line joining two points P and Q is of constant length a and the velocities of P and Q are in directions which make angles \alpha and \beta with PQ.Prove that the angular velocity of PQ is \frac{u \sin (\alpha-\beta)}{a \cos \beta} ,where u is the velocity of P.)
Solution:PQ का कोणीय वेग Q के सापेक्ष है
\frac{u \sin \alpha-v \sin \beta}{PQ} \cdots(1)
P का Q के सापेक्ष वेग PQ के अनुदिश है
=u \cos \alpha-v \cos \beta
परन्तु PQ अचर लम्बाई हैः
अतः PQ के अनुदिश इसके घटक शून्य हो जाते हैंः
\therefore u \cos \alpha-v \cos \beta=0 \\ \Rightarrow v=\frac{u \cos \alpha}{\cos \beta}
PQ का कोणीय वेग=\frac{u \sin \alpha-u \frac{\cos \alpha}{\cos \beta} \sin \beta}{a} \\ =\frac{u \sin (\alpha-\beta)}{a \cos \beta}
Illustration:11.एक चलती हुई रेलगाड़ी पर उसकी गति की दिशा से कोण बनाते हुए एक सन्दूक की गोली चलाई जाती है।गोली एक डिब्बे में इन्जिन से दूर वाले कोने से अन्दर घुसती है और उस विकर्ण के सामने वाले कोने से बाहर निकलती है।यदि रेलगाड़ी का वेग u मीटर प्रति सेकण्ड है और डिब्बे की लम्बाई तथा चौड़ाई a व b मीटर है तो सिद्ध कीजिए कि डिब्बे से गोली का गुजरने का समय \frac{(b \cot \alpha-a)}{u} सेकण्ड है।
(A pistol shot is fired on a running train at an angle with its direction of motion.The shot enters a carriage at a corner farthest from the engine and passes out at the diagonally opposite corner.If u be the velocity of the train in meters per second and a,b are the length and breadth of the compartments in meters,show that the time of the shot takes to pass through the compartment is \frac{(b \cot \alpha-a)}{u} sec .)
Solution:गोली डिब्बे को विकर्णत क्रास करती है,यदि सापेक्ष वेग की दिशा \theta है तो:
\tan \theta=\frac{a}{b} \\ V \cos \theta=u_1 \cos \beta-u
तथा V \sin \theta=u_1 \sin \beta \cdots(1)
रेल का उर्ध्वाधर वेग नहीं है
\therefore \tan \theta=\frac{u_1 \sin \beta}{u_1 \cos \beta-u}=\frac{a}{b} \\ \sin \beta=\sin \alpha (दिया है)
\Rightarrow \frac{u_1 \sin \alpha}{u_1 \cos \beta-u}=\frac{a}{b} \\ \Rightarrow \sqrt{1-\cos ^2 \beta}=\sin \alpha \\ \Rightarrow 1-\cos ^2 \beta=\sin ^2 \alpha \\ \Rightarrow \cos ^2 \beta=1-\sin ^2 \alpha \\ \Rightarrow \cos^2 \beta=\cos ^2 \alpha \\ \Rightarrow \cos \beta=\cos \alpha \\ \Rightarrow \frac{u_1 \sin \alpha}{u_1 \cos \alpha-u}=\frac{a}{b} \\ \Rightarrow b u_1 \sin \alpha=a u_1 \cos \alpha-a u \\ \Rightarrow a u_1 \cos \alpha-b u_1 \sin \alpha=a u \\ \Rightarrow u_1=\frac{a u}{a \cos \alpha-b \sin \alpha} \cdots(2)
उर्ध्वाधर घटक=u_1 \sin \beta तथा उर्ध्वाधर दूरी a मीटर है
\therefore a=u_1 \sin \beta \cdot t \\ \Rightarrow a=\frac{a u}{a \cos \alpha-b \sin \alpha} \sin \alpha \cdot t [(2) से]
\Rightarrow t=\frac{a \cos \alpha-b \sin \alpha}{u \sin \alpha} \\ \Rightarrow t=\left(\frac{a \cot \alpha-b}{u}\right)
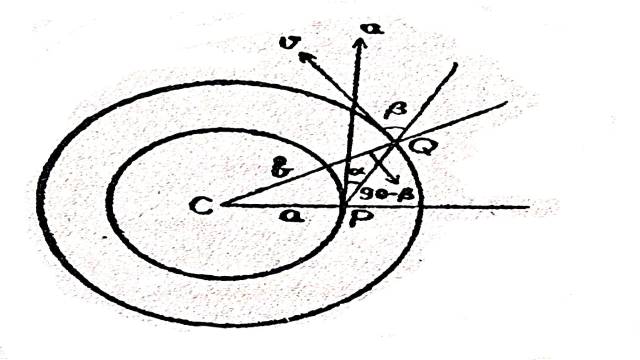
Illustration:12.दो कण a तथा b त्रिज्या वाले सहकेन्द्रीय वृत्तों में क्रमशः कोणीय वेगों तथा से चल रहे हैं।सिद्ध करो कि उनको मिलाने वाली रेखा,जिसकी लम्बाई r है,का कोणीय वेग होगाः
(Two particles are describing concentric circles of radii a and b with angular velocities and respectively.Prove that the angular velocity of the line joining them when it is of the length r is):
\frac{\left(r^2+a^2-b^2\right) w+\left(r^2-a^2+b^2\right) w^{\prime}}{2 r^2}
Solution:यदि u तथा v,P और Q के रैखिक वेग हों तो
\omega=\frac{u}{a} तथा \omega^{\prime}=\frac{v}{b} \cdots(1)
माना वेग,PQ के साथ कोण \alpha व \beta बनाते हैं;तब रेखा PQ का कोणीय वेग अर्थात् P का Q के सापेक्ष वेग हैः
=\frac{\text{the component of velocity of P relative to Q} \bot \text{to PQ}}{\text{PQ}} \\ \frac{(\text { actual of } P -\text {actual of } Q) \bot \text {to PQ}}{P Q} \\ =\frac{u \sin \alpha-v \sin \beta}{r} \\ =\frac{a \omega \sin \alpha-b \omega^{\prime} \sin \beta}{r} [(1) से]
\triangle CPQ से
a^2=b^2+r^2-2 b r \cos (90-\beta) \\ \therefore b \sin \beta=\frac{b^2+r^2-a^2}{2 r} \cdots(3)
तथा b^2=a^2+r^2-2 a r \cos (90+\alpha) \\ a \sin \alpha=\frac{b^2-a^2-r^2}{2 r} \cdots(4)
(3) और (4) से (2) में मान रखने परः
=\omega \frac{\left(b^2-a^2-r^2\right)}{2 r}-\omega^{\prime} \frac{\left(b^2+r^2-a^2\right)}{2 r} \\ =-\frac{w\left(r^2+a^2-b^2\right)}{2 r}-\frac{w^{\prime}\left(b^2+r^2-a^2\right)}{2 r} \\ =-\left[ \frac{w\left(r^2+a^2-b^2\right)+w^{\prime}\left(r^2-a^2+b^2\right)}{2 r}\right]
ऋणात्मक चिन्ह की उपेक्षा करने पर :
=\frac{\left(r^2+a^2-b^2\right) \omega+\left(r^2-a^2+b^2\right) \omega^{\prime}}{2 r}
उपर्युक्त उदाहरणों के द्वारा आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration),गति विज्ञान में आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration in Dynamics) को समझ सकते हैं।
3.आपेक्षिक वेग और त्वरण के सवाल (Relative Velocity and Acceleration Questions):
(1.)किसी भी समय दो गतिमान बिंदुओं के बीच की दूरी a होती है और उनका सापेक्ष वेग V है,a की दिशा के अनुदिश तथा लंबवत क्रमशः u,v V के घटक हैं। दिखाएँ कि जब वे एक-दूसरे के सबसे निकट होते हैं तो उनकी दूरी \frac{av}{V} होती है और उनकी निकटतम दूरी पर पहुंचने से पहले जो समय व्यतीत हुआ है वह \frac{au}{V^2} है।
(The distance between two moving points at any time is a and their relative velocity is V,u being the components of V respectively along and perpendicular to the direction of a. Show that their distance when they are nearest to one another is \frac{av}{V} and the time that elapses before they arrive at their nearest distance is \frac{au}{V^2}.)
(2.)एक क्रैंक CP एक निश्चित केंद्र C के चारों ओर घूमता है जबकि कनेक्टिंग राॅड PD पीडी का अंत D (पिस्टन) पिस्टन के वेग के साथ चलने के लिए विवश होता है,D का रैखिक वेग है:
(A crank CP rotates about a fixed centre C while the end D (the piston) of the connecting rod PD is constrained to move along velocity of piston, the linear velocity of D is \omega )
-\text{CP} \cdot \frac{\sin (\theta+\phi)}{\cos \phi} \omega
उपर्युक्त सवालों को हल करने पर आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration),गति विज्ञान में आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration in Dynamics) को ठीक से समझ सकते हैं।
Also Read This Article:- Motion of a Particle in a Plane
4.आपेक्षिक वेग और त्वरण (Frequently Asked Questions Related to Relative Velocity and Acceleration),गति विज्ञान में आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration in Dynamics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
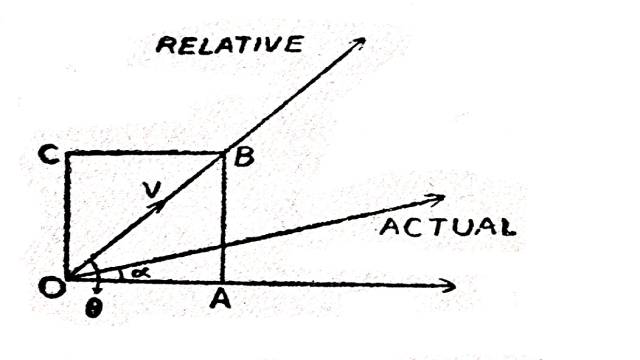
प्रश्न:1.आपेक्षिक वेग तथा रेखा AB के मध्य कोण का सूत्र लिखो। (Write the Formula of Angle between the Relative Velocity and the Line AB):
उत्तर:यदि B का A के सापेक्ष आपेक्षिक वेग V हो तथा वह AB के साथ \theta कोण बनाये,तब
V \cos \theta=v \cos \beta-u \cos \alpha
तथा V \sin \theta=v \sin \beta-u \sin \alpha
वर्ग करके जोड़ने परः
V^2=u^2+v^2-2 u v \cos (\alpha-\beta)
तथा पहले का दूसरे में भाग देने परः
\tan \theta=\frac{v \sin \beta-u \sin \alpha}{v \cos \beta-u \cos \alpha}
प्रश्न:2.आपेक्षिक कोणीय वेग का सूत्र लिखो। (Write the Formula for Relative Angular Velocity):
उत्तर:B का A के सापेक्ष आपेक्षिक कोणीय वेग=\frac{v \sin \beta-u \sin \alpha}{A B}
प्रश्न:3.आपेक्षिक वेग का सूत्र लिखो। (Write the Formula of Relative Velocity):
उत्तर: V=\sqrt{u^2+v^2-2 u v \cos (\alpha-\beta)}
उपर्युक्त प्रश्नों के उत्तर द्वारा आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration),गति विज्ञान में आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration in Dynamics) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here | |
| 7. | click here |
Relative Velocity and Acceleration
आपेक्षिक वेग और त्वरण
(Relative Velocity and Acceleration)
Relative Velocity and Acceleration
आपेक्षिक वेग और त्वरण (Relative Velocity and Acceleration) के इस आर्टिकल में
आपेक्षिक वेग और त्वरण से सम्बन्धित सवालों को हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.