Prove that by Contour Integration
1.परिरेखा समाकलन द्वारा सिद्ध कीजिए (Prove that by Contour Integration),परिरेखा समाकलन (Contour Integration):
परिरेखा समाकलन द्वारा सिद्ध कीजिए (Prove that by Contour Integration) के इस आर्टिकल में ऐसे समाकलों का मान ज्ञात करना सीखेंगे जिन्हें वर्ग,आयत,वृत्त के चतुर्थांश आदि परिरेखा का प्रयोग किया गया हो।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Use Method of Contour Integration
2.परिरेखा समाकलन द्वारा सिद्ध कीजिए के उदाहरण (Prove that by Contour Integration Examples):
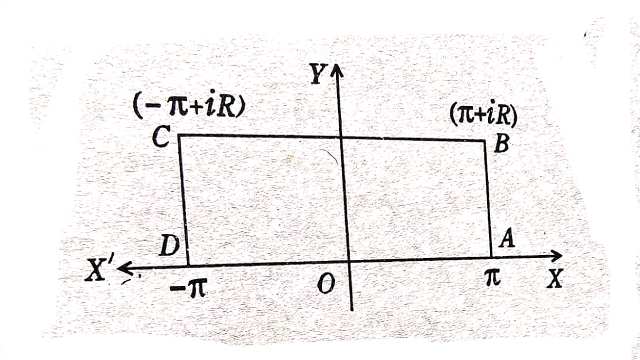
Example:1.एक आयत जिसके सम्मिश्र तल में शीर्ष बिन्दु z= \pm \pi, \pm \pi i R हैं,पर \frac{z}{1-a e^{i z}} का समाकलन करते हुए सिद्ध कीजिए यदि a \geq 1
(Integrating \frac{z}{1-a e^{i z}} round the rectangle with vertices at z= \pm \pi, \pm \pi i R ,prove that if a \geq 1)
\int_0^\pi \frac{a x sin x}{1-2 a \cos x+a^2} d x=\pi \log \left(1+\frac{1}{a}\right)
इस समाकल का मान क्या होगा जब 0 < a < 1
(What is the value of this integral when?)
Solution:समाकल \int_c \frac{z}{1-a e^{-i z}} d z=\int_c f(z) d z पर विचार करो,जहाँ C शीर्षों x= \pm \pi , y=0,y=R वाला आयत है।f(z) में सरल अनन्तक हैं जो निम्न द्वारा दिए गए हैं:
e^{i z}=a=\exp (\log a+2 n \pi i) \\ \Rightarrow z=-i(\log a+2 n \pi i), n=0,\pm1, \pm 2 \ldots
यदि 0< a< 1 यहाँ केवल z=-i \log a अनन्तक है जो आयत C के भीतर स्थित है।यदि a >1 तो C के अन्दर कोई अनन्तक नहीं है।
z=-i \log a पर अवशेष है:
\left[\frac{z}{D\left(1-a e^{-i z}\right)}\right]_{z=-i \log a}=\frac{-i \log a}{a i \exp (-\log a)}=-\log a
कोशी अवशेष प्रमेय द्वारा
\int_c f(z) d z=\int_{-\pi}^\pi f(x) d x+\int_0^R f(\pi+i y) i dy+\int_\pi^{-\pi} f(x+i R) d x+\int_R^0 f(-\pi+i y) i d y=2 \pi i(-\log a) \ldots(1)
अब \int_\pi^{-\pi} f(x+i R) d x \leq \int_\pi^{-\pi} \frac{|x+i R|}{|1-a \exp (-i x+R)|} d x \\ \leq \int_\pi^{-\pi} \frac{|x|+R}{a e^R-1} d x \rightarrow 0 \operatorname{as} R \rightarrow \infty \\ \int_{-\pi}^\pi f(x) d x=\int_{-\pi}^\pi \frac{x d x}{1-a e^{-i x}}=\int_{-\pi}^0 \frac{x d x}{1-a e^{-i x}} +\int_0^\pi \frac{x d x}{1-a e^{-i x}}
प्रथम समाकल में x की जगह -x रखने परः
I=\int_\pi^0 \frac{x d x}{1-a e^{i x}}+\int_0^\pi \frac{x d x}{1-a e^{-i x}}=\int_0^\pi x\left(\frac{1}{1-a e^{-i x}}-\frac{1}{1-a e^{i x}}\right) d x \\ =\int_0^\pi \frac{-x a\left(e^{i x}-e^{-i x}\right)}{1-a\left(e^{i x}+e^{-i x}\right)+a^2} d x = \int^{\pi}_0 \frac{-2a ix \sin x}{1-2a \cos x +a^2} dx\\ \underset{R \rightarrow \infty}{\lim } \left[\int_0^R f(\pi+i y) i d y+\int_R^{0} f(-\pi+i y)i d y\right]\\ =\int_0^{\infty} \left[\frac{\pi+i y}{1-a \exp (-i \pi+y)}-\frac{(-\pi+i y)}{1-a \exp (\pi i+y)}\right] i d y \\ =\int_0^{\infty} \frac{2 \pi}{1+a e^y}i d y=\int_0^{\infty} \frac{2 \pi i e^{-y}}{e^{-y}+a} d y \\=-2 \pi i\left[\log \left(e^{-y}+a\right) \right]_0^{\infty} =2 \pi i[\log (1+\infty)-\log a]
as R \rightarrow \infty , (1) से :
\int_0^\pi \frac{-2 i x a \sin x}{1-2 a \cos x+a^2}d x+2 \pi i[\log (1+a)-\log a]= 2 \pi i (- \log a) , 0 < a <1 \\ \Rightarrow \int_0^\pi \frac{x a \sin x}{i-2 a \cos x+a^2} d x=\pi \log (1+a)
जब a > 1 ,हम (1) से रखते हैं
\int_0^\pi \frac{-2 i x a \sin x}{1-2 a \cos x+a^2} d x+2 \pi[\log (1+a)-\log a]=0 \\ \Rightarrow \int_0^\pi \frac{a x \sin x}{1-2 a \cos x+a^2} d x=\pi \log \left(1+\frac{1}{a}\right)
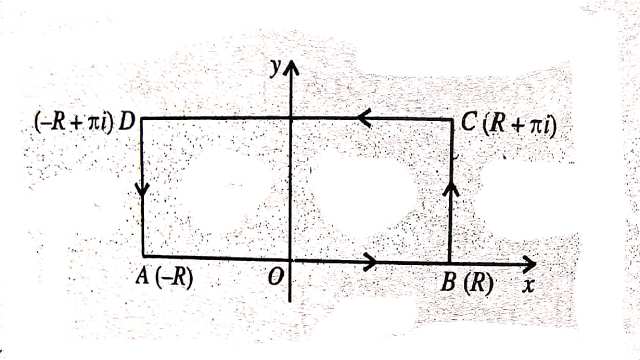
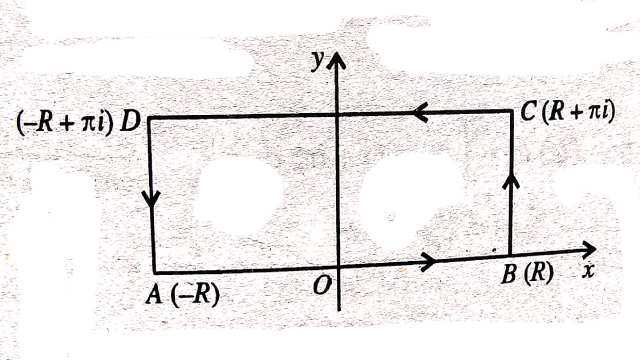
Example:2.एक आयत जिसके सम्मिश्र तल में शीर्ष z= \pm R , z= \pm R+\pi i हैं,पर \frac{z e^{a z}}{1+e^{a z}} का समाकल करते हुए,सिद्ध कीजिए:
(By integrating \frac{z e^{a z}}{1+e^{a z}} round a rectangle whose vertices are at z= \pm R , z= \pm R+\pi i , prove that)
\int_0^{\infty} \frac{t^{a-1} \log t}{1+t^2} d t=-\frac{\pi^2}{4} \frac{\cos \left(\frac{\pi a}{2}\right)}{\sin ^2\left(\frac{\pi a}{2}\right)} where o < a <2 )
Solution:माना f(z)=\frac{z e^{a z}}{1+e^{a z}} ,
समाकल पर विचार करो,जहाँ C शीर्ष -R,R , R+ \pi , -R+i \pi वाला ABCD आयत है।
f(z) के अनन्तक दिए जाते हैं:
1+e^{2 z}=0 \\ \Rightarrow e^{2 z}=-1=e^{(2 n+1) \pi i} \\ \Rightarrow 2 z=(2 n+1) \pi i \\ \Rightarrow z=\left(n+\frac{1}{2}\right) \pi i, जहाँ n=0, \pm 1, \pm 2, \pm 3
f(z) का C के अन्दर z=\frac{\pi i}{2} साधारण अनन्तक हैः
z=\frac{\pi i}{2} पर अवशेष=\underset{z \rightarrow \frac{\pi i}{2}}{\lim} \frac{\phi(z)}{\psi^{\prime}(z)} जहाँ f(z)=\frac{\phi(z)}{\psi^{\prime}(z)} \\ =\underset{z \rightarrow \frac{\pi i}{2}}{\lim} \frac{z e^{a z}}{2 e^{2 z}}=\frac{\pi i}{2} \cdot \frac{e^{\frac{i \pi a}{2}}}{2 e^{i \pi}}=-\frac{i \pi}{4} e^{\frac{i \pi a}{2}}
कोशी अवशेष प्रमेय द्वारा
\int_c f(z) dz=2 \pi i \cdot \operatorname{Res}\left(z=\frac{\pi i}{2}\right) \\ =2 \pi i \cdot\left(-\frac{\pi i}{4}\right) e^{\frac{i \pi a}{2}} \\ \Rightarrow \left[\int_{A B}+\int_{B C}+\int_{C D}+\int_{D A}\right] f(z) d z=\frac{\pi^2}{2} e^{\frac{i \pi a}{2}} \ldots(1) \\ \Rightarrow \int_{A B} f(z) d z=\int_{-R}^R f(x) d x=\int_{-R}^R \frac{x e^{a x}}{1+e^{2 x}} d x \ldots(2) \\ \int_{B C} f(z) d z=\int_0^\pi f(R+i y) i d y= \int_0^{\pi} \frac{(R+i y) e^{a(R+i y)}}{1+e^{2(R+i y)}} idy \\ =\int_0^\pi \frac{(R+i y) e^{a R} e^{i a y} i d y}{1+e^{2 R} \cdot e^{2 i y}} \\ \Rightarrow\left|\int_{B C} f(z) d z\right| \leq \int_0^\pi \frac{(R+y) e^{a R} d y}{e^{2 R}-1}=\frac{e^{a R}}{e^{2R-1}}\left[R y+\frac{y^2}{2}\right]_0^\pi \\=\left(R \pi+\frac{\pi^2}{2}\right) \cdot \frac{1}{e^{(2-a) R}-e^{-a R}} \rightarrow 0 \text { as } R \rightarrow \infty
for 2-a > 0 ; a >0\\ \therefore \underset{R \rightarrow \infty}{\lim} \int_{B C} f(z) d z=0 \cdots(3)
इसी प्रकार
\underset{R \rightarrow \infty}{\lim} \int_{D A} f(z) d z=0 \ldots(4) \\ \int_{C D} f(z) d z =\int_R^{-R} f(x+i \pi) d x=\int_R^{-R} \frac{(x+i \pi) e^{a(x+i \pi)}}{1+e^{2(x+i \pi)}} d x \\=-\int_{-R}^R \frac{(x+i \pi) e^{a x} \cdot e^{i \pi) a}}{1+e^{2 x}} d x \ldots(5)
(1) में R \rightarrow \infty प्रयोग करने और (2),(3),(4) तथा (5) से हम प्राप्त करते हैं:
\int_{-\infty}^{\infty} \frac{x e^{a x}}{1+e^{2 x}} d x-\int_{-\infty}^{\infty} \frac{(x+i \pi) e^{d x} \cdot e^{i \pi a}}{1+e^{2 x}} d x=\frac{\pi^2}{2} e^{\frac{i \pi a}{2}}
दोनों पक्षों के वास्तविक और काल्पनिक भागों की तुलना करने परः
\int_{-\infty}^{\infty} \frac{e^{a x}}{1+e^{2 x}}[x(1-\cos \pi a)+\pi \sin \pi a] d x=\frac{\pi^2}{2} \cos \left(\frac{\pi a}{2}\right) \ldots(6) \\ \int_{-\infty}^{\infty} \frac{e^{a x}}{1+e^{2 x}}[-x \sin \pi a-\pi \cos \pi a] d x=\frac{\pi^2}{2} \sin \left(\frac{\pi a}{2}\right) \ldots(7)
(6) को \cos \pi a से,(7) को \sin \pi a से गुणा करके जोड़ने परः
\int_{-\infty}^{\infty} \frac{e^{a x}}{1+e^{2 x}}\left[x\left(\cos \pi a-\cos ^2 \pi a-\sin ^2 \pi a\right) d x\right]=\frac{\pi^2}{2}\left[\cos \pi a \cdot \cos \frac{\pi a}{2}+\sin \pi \sin \frac{\pi a}{2}\right] \\ \int_{-\infty}^{\infty} \frac{x e^{8 x}}{1+e^{2 x}}(\cos \pi a-1) d x=\frac{\pi^2}{2} \cos \left(\pi a-\frac{\pi a}{2}\right) \\ \Rightarrow \int_{-\infty}^{\infty} \frac{x e^{a x}}{1+e^{2 x}} d x=-\frac{\pi^2}{2} \cdot \frac{\cos \left(\frac{\pi a}{2}\right)}{2 \sin ^2\left(\frac{\pi a}{2}\right)}
e^x=t रखने पर ताकि x=\log t, d x=\frac{d t}{t} \\ x=\infty \Rightarrow t=\infty तथा x=-\infty \Rightarrow t=0 \\ \int_0^{\infty} \frac{t^{a-1} \log t}{1+t^2} d t=-\frac{\pi^2}{4} \frac{\cos \left(\frac{\pi a}{2}\right)}{\sin ^2\left(\frac{\pi a}{2}\right)}
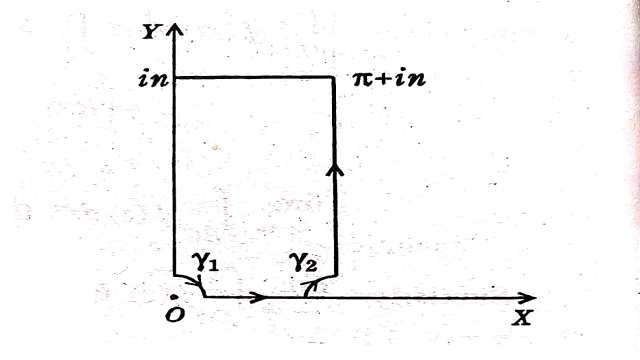
Example:3.फलन \frac{e^{a z}}{e^{-2 i z}-1} को उपयुक्त परिरेखा पर समाकलन करते हुए सिद्ध कीजिए कि
(By integrating \frac{e^{a z}}{e^{-2 i z}-1} round a suitable contour,show that)
\int_0^{\infty} \frac{\sin a y}{e^{2 y}-1} d y=\frac{\pi}{4} \operatorname{coth} \frac{\pi a}{2}-\frac{1}{2 a}
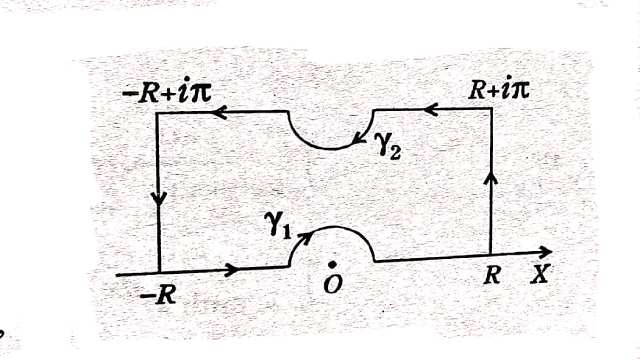
Solution:समाकल \int_c \frac{e^{a z}}{e^{-2iz-1}} d z=\int_c f(z) d z पर विचार करो,जहाँ C चित्र में दिखाई गई परिरेखा है।
फलन f(z),C के अन्दर नियमित है अतः अवशेष प्रमेय द्वारा
\int_c f(z) d z= \int_{\rho_1}^{\pi-\rho_2} f(x) d x+\int_{\gamma_2} f(z) dz + \int_{\rho_2}^n f(\pi+i y) id y+\int_\pi^0 f(x+i n) d x +\int_n^{\rho_1} f(i y) i d y+\int_{\gamma_1} f(z) d z=0 \\ \Rightarrow I_1+I_2+I_3+I_4+I_5+I_6=0 \\ \underset{z \rightarrow 0}{\lim} z f(z)=\underset{z \rightarrow 0}{\lim} \frac{z e^{a z}}{e^{-2 i z}-1}=-\frac{1}{2 i} \\ \therefore \underset{\rho_{1} \rightarrow 0}{\lim} I_6=i\left(0-\frac{\pi}{2}\right)\left(-\frac{1}{2 i}\right)=\frac{\pi}{4} \\ \underset{z \rightarrow \pi}{\lim} (z-\pi) f(z)=\underset{z \rightarrow \pi}{\lim} \frac{(z-\pi) e^{a z}}{e^{-2 i z}-1} \\ \underset{z \rightarrow \pi}{\lim} \frac{e^{a z}+(z-\pi) a e^{a z}}{-2 i \cdot e^{-2 i z}}=\frac{e^{a \pi}}{-2 i} \\ \therefore \underset{\rho_{2} \rightarrow 0}{\lim} I_2=i\left(0-\frac{\pi}{2}\right)\left(\frac{e^{a \pi}}{-2 i}\right)=\frac{\pi}{4} e^{a \pi} \\ \underset{\rho_{1} \rightarrow 0 , \rho_{2} \rightarrow 0}{\lim} I_1=\underset{\rho_{1} \rightarrow 0 , \rho_{2} \rightarrow 0}{\lim} \int_{\rho_2 \rightarrow 0}^{\pi-\rho_2} \frac{e^{ax}}{e^{-2 i x}-1} d x= \int_0^\pi \frac{e^{a x}}{e^{-2 i x}-1} d x \\ =-\int_0^\pi \frac{e^{a x}\left(1-e^{2i x}\right)}{\left(1-e^{2i x}\right) \left(1-e^{-2 i x}\right)} d x=-\int_0^\pi \frac{e^{a x}\left(1-e^{2 i x}\right)}{2(1-\cos 2 x)} d x \\ =-\frac{1}{4} \int_0^\pi \frac{e^{a x}\left(1-e^{2 i x}\right)}{\sin ^2 x} d x \\ \underset{n \rightarrow \infty , \rho_{2} \rightarrow 0}{\lim} I_3=\underset{n \rightarrow \infty }{\lim} \int_0^n \frac{\exp a(\pi+i y) i d y}{\exp [-2 i(\pi+i y)]-1}=\int_{0}^{\infty} \frac{e^{a \pi} e^{a i y}}{e^{2 y}-1} dy \\ \left|I_4\right|= \left|\int_\pi^0 \frac{e^{a(x+i n)}}{e^{-2i(x+i n)}-1} d x\right| \leq \int_\pi^0 \frac{\left|e^{a x} e^{iax}\right| }{\left|e^{-2i(x+i n)}\right|-1} dx \\ =\int_\pi^0 \frac{e^{a x}}{e^{2 n}-1} \rightarrow 0 \text { as } n \rightarrow \infty
तथा \underset{\substack{n \rightarrow \infty \\ \rho_1 \rightarrow 0}}{\lim} I_5=\underset{n \rightarrow \infty}{\lim} \int_n^0 \frac{e^{a i y} i d y}{e^{2 y}-1}=\int_{\infty}^0 \frac{e^{iay} i d y}{e^{2 y}-1}
इस प्रकार (1) सेः
–\frac{1}{4} \int_0^\pi \frac{e^{a x}\left(1-e^{i 2 x}\right)}{\sin ^2 x} d x+\frac{\pi}{4} e^{a \pi}+ \int_0^{\infty} \frac{e^{a \pi} e^{i a y}}{e^{2 y}-1} i dy+\int^0_{\infty} \frac{e^{i a y}}{e^{2 y}-1} i dy+ \frac{\pi}{4}=0 \\ \Rightarrow \frac{\pi}{4}\left(1+e^{a \pi}\right)-\frac{1}{4} \int_0^\pi \frac{e^{a x}\left(1-e^{i 2 x}\right)}{\sin ^2 x} d x+ \int_0^{\infty} \frac{\left(e^{a \pi}-1\right) i e^{i a y} }{e^{2 y}-1}d y=0
दोनों पक्षों के वास्तविक भागों की तुलना करने परः
\left(1-e^{a \pi}\right) \int_0^{\infty} \frac{\sin a y}{e^{2 y}-1} d y+\frac{\pi}{4}\left(1+e^{a \pi} \right)-\int_0^\pi \frac{e^{a x}(1-\cos 2 x)}{4 \sin 2 x} d x=0 \\ \Rightarrow \left(1-e^{a \pi}\right) \int_0^{\infty} \frac{\sin a y}{e^{2 y}-1} d y=\frac{1}{2 a}\left[e^{a x}\right]_0^\pi-\frac{\pi}{4}\left(1+e^{a \pi}\right) \\ =\frac{1}{2 a}\left(e^{a \pi}-1\right)-\frac{\pi}{4}\left(1+e^{a \pi}\right) \\ \therefore \int_0^{\infty} \frac{\sin ay dy}{e^{2 y}-1}=-\frac{1}{2 a}-\frac{\pi}{4} \cdot \frac{1+e^{a \pi}}{1-e^{a \pi}}=\frac{\pi}{4} \operatorname{coth} \frac{a \pi}{2} -\frac{1}{2a}
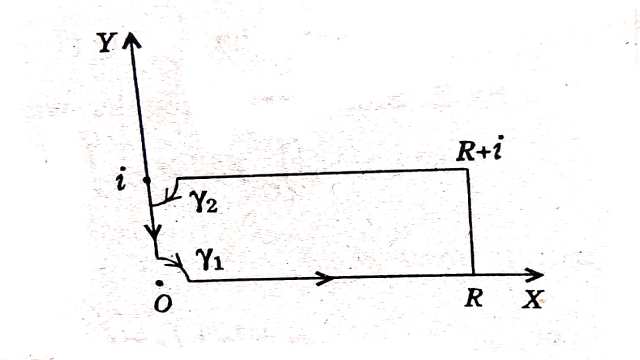
Example:4.0 और i पर इंडेंट किए गए भुजाओं x=0,x=R,y=0,y=1 के आयत के चारों ओर \frac{e^{i a z}}{e^{2 \pi z}-1} (a वास्तविक है) का समाकलन करते हुए,सिद्ध करो कि
(Integrating \frac{e^{i a z}}{e^{2 \pi z}-1} , (a is real) round the rectangle of sides x=0,x=R,y=0,y=1 indented at 0 and i,prove that)
\int_0^{\infty} \frac{\sin a x}{e^{2 \pi x}-1}= \frac{1}{4} \operatorname{coth} \frac{1}{2} a-\frac{1}{2} a
Solution: \int_c \frac{e^{i a z}}{e^{2 \pi z}-1} d z=\int_c f(z) d z पर विचार करो,जहाँ C चित्र में दिखाई गई परिरेखा है।जबकि f(z),C के अन्दर नियमित है अतः अवशेष प्रमेय द्वारा हम रखते हैं:
\int_c f(z) d z=\int_{\gamma_1} f(z) d z+\int_{\rho_1}^R f(x) d x+\int_0^1 f(R+i y) i d y + \int_R^{\rho_2} f(R+i) d x+\int_{\gamma_2} f(z) d z+\int_{1-\rho_2}^{\rho_2} f(i y) i d y=0 \\ \Rightarrow I_1+I_2+I_3+I_4+I_5+I_6=0 \cdots(1)
जबकि \underset{z \rightarrow 0}{\lim} z f(z)=\underset{z \rightarrow 0}{\lim} z \frac{e^{i a z}}{e^{2 n \pi}-1}= \underset{z \rightarrow 0}{\lim} \frac{e^{i a z}+i a z e^{i a z}}{2 \pi e^{2 \pi z}}=\frac{1}{2 a} \\ \therefore \underset{\rho_1 \rightarrow 0}{\lim} I_1=i\left(0-\frac{\pi}{2}\right) \frac{1}{2 \pi}=\frac{-i}{4} \\ \underset{z \rightarrow i}{\lim} (z-i) f(z)=\lim _{z \rightarrow i} \frac{(z-i) e^{i a z}}{e^{2 \pi z}-1}= \underset{z \rightarrow i}{\lim} \frac{e^{i a z}+(z-i) i a e^{i a z}}{2 \pi e^{2 \pi z}}=\frac{e^{-a}}{2 \pi} \\ \therefore \underset{\rho_2 \rightarrow 0}{\lim} I_5=-\frac{i}{4} e^{-a} \\ \left|I_3\right|=\left|\int_0^1 \frac{\exp [ia(R+i y)] i d y}{\exp [2 \pi(R+i y)-1}\right| \leq \int_0^1 \frac{e^{-a y}}{\exp 2 R \pi-1} d y \rightarrow 0 \text { as } R \rightarrow \infty
इस प्रकार R \rightarrow \infty, \rho_1 \rightarrow 0, \rho_2 \rightarrow 0, (1) से रखते हैं:
\int_0^{\infty} f(x) d x+\int_{\infty}^0 f(x+i) d x+\int_1^0 f(i y) i d y=\frac{i}{4}\left(1+e^{-a}\right) \\ \Rightarrow \int_0^{\infty} \frac{e^{i a x}}{e^{2 \pi x}-1} d x+\int_{\infty}^0 \frac{e^{i a(x+i)}}{e^{2 \pi(x+i)}} d x+\int_1^0 \frac{e^{-a y}}{e^{2 \pi i y}-1} d y=\frac{i}{4}\left(1+e^{-a}\right) \\ \Rightarrow \int_0^{\infty} \frac{\left(1-e^{-a}\right) e^{i a x}}{e^{2 \pi x}-1} d x=\frac{i}{4}\left(1+e^{-a}\right)+ \int_0^1 \frac{e^{-ay}-e^{-i \pi y}}{e^{i \pi y}-e^{-i \pi y}} dy=\frac{i}{4}\left(1+e^{-a}\right)+\int_0^1 \frac{e^{-a y} e^{-i \pi y}}{2 \sin \pi y} d y
दोनों पक्षों के काल्पनिक भागों की तुलना करने परः
\int_0^{\infty} \frac{\sin a x}{e^{2 \pi x}-1} d x=\frac{1}{4} \cdot \frac{1+e^{-a}}{1-e^{-a}}-\frac{1}{1-e^{-a}} \int_0^1 \frac{e^{-a y}}{2} d y =\frac{1}{4} \operatorname{coth}\left(\frac{a}{2}\right)-\frac{1}{2 a} \frac{1-e^{-a}}{\left(1-e^{-a}\right)}=\frac{1}{4} \operatorname{coth} \frac{a}{2} - \frac{1}{2 a}
Example:5.परिरेखा समाकलन द्वारा सिद्ध करो कि
(By contour integration, prove that)
\int_0^{\infty} \frac{\cosh a x}{\cosh x} d x=\frac{\pi}{2} \sec \left(\frac{\pi a}{2}\right) if |a|<1
Solution:माना f(z)=\frac{e^{a z}}{\cosh z}=\frac{2 e^{a z}}{e^z+e^{-z}}
f(z) के अनन्तक दिए जाते हैं:
e^z+e^{-z}=0 \\ \Rightarrow e^{2 z}+1=0 \Rightarrow e^{2 z}=-1 \\ =e^{(2 n+1) \pi i} \\ \Rightarrow z=\left(n+\frac{1}{2}\right) \pi i जहाँ n=0, \pm 1, \pm 2, \ldots \\ \Rightarrow z= \pm \frac{i \pi}{2}, \pm \frac{3 i \pi}{2}, \ldots
\int_C f(z) d z पर विचार करो,जहाँ C,ABCD आयत है जो चित्र में दिखाया गया हैः
C के अन्दर z=\frac{i \pi}{2} केवल एक अनन्तक है।
z=\frac{i \pi}{2} पर अवशेष= \underset{z \rightarrow \frac{i \pi}{2}}{\lim} \frac{\phi(z)}{\psi^{\prime}(z)} जहाँ f=\frac{\phi}{\psi} \\ =\underset{z \rightarrow \frac{i \pi}{2}}{\lim} \frac{e^{a z}}{\sinh z}=\frac{e^{\frac{i \pi g}{2}}}{\sinh \left(\frac{i \pi}{2}\right)} \\=\frac{2 e^{\frac{i \pi a}{2}}}{e^{\frac{i \pi}{2}}-e^{-\frac{i \pi}{2}}}=\frac{2 e^{\frac{i \pi a}{2}}}{i+i}=-i e^{\frac{i \pi}{a}}
कोशी अवशेष प्रमेय सेः
\int_C f(z) d z=2 \pi i \cdot \operatorname{Res}\left(z=\frac{i \pi}{2}\right)=2 \pi i(-i) e^{\frac{i \pi a}{2}} \\ \Rightarrow \left| \int_{AB}+\int_{BC}+\int_{CD}+\int_{DA}\right| f(z) d z=2 \pi e^{\frac{i \pi g}{2}} \cdots(1) \\ \int_{A B} f(z) d z=\int_{-R}^R f(x) d x=\int_{-R}^R \frac{e^{a x} d x}{\cosh x} \cdots(2) \\ \Rightarrow \int_{B C} f(z) d z=\int_0^\pi \frac{e^{a(R+i y)}}{\cosh (R+i y)} i dy \\ 2 \int_0^\pi \frac{e^{a R} \cdot e^{i a y} i d y}{e^R \cdot e^{i y}+e^{-R} \cdot e^{-i y}} \\ \therefore \left|\int_{B C} f(z) d z\right| \leq 2 \int_0^\pi \frac{e^{a R} d y}{e^R-e^{-R}} \\ =2 \pi \frac{1}{e^{(1-a) R}-e^{-(1+a) R}} \rightarrow 0 \text { as } R \rightarrow \infty \\ \left[\because 1-a>0,-(1+a)<0 \right] \\ \therefore \lim _{R \rightarrow \infty} \int_{B C} f(z) d z=0 \cdots(3)
इसी प्रकार \underset{R \rightarrow \infty}{\lim} \int_{D A} f(z) d z=0 \cdots(4) \\ \int_{C D} f(z) d z=\int_R^{-R} f(x+i \pi) d x=\int_R^{-R} \frac{e^a(x+i \pi)}{\cosh (x+i \pi)} d x \\ \cosh (x+i \pi) \equiv \frac{e^{x+i \pi}+e^{-(x+i \pi)}}{2}=\frac{-e^x-e^{-x}}{2}=-\cosh x \\ \therefore \int_{C D} f(z) d z=-\int_{-R}^R \frac{e^{a x} \cdot e^{i \pi a}}{-\cosh x} d x \cdots(5)
(1) में R \rightarrow \infty बनाने पर तथा (2),(3),(4),(5) से हम प्राप्त करते हैं:
\int_{-\infty}^{\infty} \frac{e^{a x}}{\cosh x} d x+\int_{-\infty}^{\infty} \frac{e^{a x} \cdot e^{i \pi a}}{\cosh x} d x=2 \pi e^{\frac{i \pi a}{2}} \\ \Rightarrow \int_{-\infty}^{\infty} \frac{e^{a x}}{\cosh x} d x= \frac{2 \pi \cdot e^{\frac{i \pi a}{2}}}{1+e^{i \pi a}} \\ =\frac{2 \pi}{e^{\frac{i \pi a}{2}}+e^{-\frac{i \pi a}{2}}} =\frac{\pi}{\cos \left(\frac{\pi a}{2}\right)} \\ \Rightarrow \int_{-\infty}^0 \frac{e^{a x}}{\cosh x} dx+\int_0^{\infty} \frac{e^{a x}}{\cosh x} d x=\pi \sec \left(\frac{\pi a}{2}\right)
प्रथम समाकल में x को -x से परिवर्तित करने पर,हम प्राप्त करते हैं:
\int_{\infty}^{\infty} \frac{e^{-a x}(-d x)}{\cosh x}+\int_0^{\infty} \frac{e^{a x} d x}{\cosh x}=\pi \sec \left(\frac{\pi a}{2}\right) \\ \Rightarrow \int_0^{\infty} \frac{e^{a x}+e^{-a x}}{\cosh x} d x=2 \int_0^{\infty} \frac{\cosh a x}{\cosh x} dx \\ \Rightarrow \int_0^{\infty} \frac{\cosh a x}{\cosh x} d x=\frac{\pi}{2} \sec \left(\frac{\pi a}{2}\right)
Example:6.एक आयत जिसके सम्मिश्र तल में शीर्ष बिन्दु \pm R, \pm R+i \pi हैं पर \frac{e^{i \alpha z}}{\sinh z} का समाकलन करते हुए सिद्ध कीजिए:
(Integrate \frac{e^{i \alpha z}}{\sinh z} round a suitable indented rectangle with vertices \pm R, \pm R+i \pi and show that)
\int_0^{\infty} \frac{\sin \alpha x}{\sinh x} d x=\frac{\pi}{2}\left(\frac{e^{\alpha \pi}-1}{e^{ \alpha \pi}+1}\right)
बशर्ते की काल्पनिक भाग -1 और 1 के बीच स्थित हों
(Provided that the imaginary part lies between -1 and 1)
Solution: \int_c f(z) d z=\int_c \frac{e^{i \alpha z}}{\sinh z} dz पर विचार करो,जहाँ C आयत है जिसके शीर्ष \pm R, \pm R+i \pi हैं और z=0 तथा i \pi पर इंडेंट किया गया है।
f(z) के अनन्तक दिए जाते हैं:
\sinh (z)=0 \Rightarrow e^z-e^{-z}=0 \\ \Rightarrow e^{2 z}-1=0 \Rightarrow e^{2 z}=1=e^{2 n \pi i} \\ \Rightarrow z=n \pi i, n=0, \pm 1, \pm 2 \ldots
ये f(z) के साधारण अनन्तक हैं और इनमें से कोई भी C के अन्दर स्थित नहीं है।
कोशी अवशेष प्रमेय से हम रखते हैं:
\int_C f(z) d z=\int_{-R}^{-\rho} f(x) d x+\int_{\gamma_1} f(z) d z+\int_{\rho_1}^R f(x) d x +\int_0^\pi f(R+i y) i d y+\int_R^{\rho_2} f(x+i \pi) d x+\int_{\gamma_2} f(z) dz+\int_{-\rho_2}^{-R} f(x+i \pi) d x+\int_\pi^0 f(-R+i y) i d y=0 \cdots(1) \\ \left|\int_0^\pi f(R+i y) \cdot i d y\right| \leq \int_0^\pi \left|\frac{e^{i \alpha(R+i y)} i d y}{\sinh (R+i y)}\right| \\ \leq \int_0^\pi \frac{e^{-\alpha y} d y}{|\sinh R \cos y+i \cosh R \sin y|} \\ \leq \int_0^\pi \frac{e^{-\alpha y} d y}{\sinh \cos y-\cosh R \sin y} \\ = \int_0^\pi \frac{2 e^{-\alpha y} d y}{\left(e^R-e^{-R}\right) \cos y-\left(e^R+e^{-R}\right) \sin y} \\ =\int_0^\pi \frac{2 e^{-\alpha y} d y}{e^R(\cos y-\sin y)-e^{-R}(\cos y+\sin y)}
इसी प्रकार \int_\pi^0 f(-R+i y) i d y \rightarrow 0 as R \rightarrow \infty
जबकि \underset{z \rightarrow 0}{\lim} z f(z)=\underset{z \rightarrow 0}{\lim} \frac{z e^{i \alpha} z}{\sinh z}=1 \\ \therefore \underset{\rho_1 \rightarrow 0}{\lim} \int_{\gamma_1} f(z) d z=i(0-\pi) 1=-i \pi
जबकि \underset{z \rightarrow i \pi}{\lim} (z-i \pi) f(z)=\underset{z \rightarrow i \pi}{\lim}(z-\pi i) \frac{e^{i \alpha z}}{\sinh z}=-e^{-\alpha \pi} \\ \underset{\rho_2 \rightarrow 0}{\lim} \rightarrow 0 \int_{\gamma_2} f(z) d z=i(0-\pi)\left(-e^{-\alpha \pi}\right)=i \pi e^{-\alpha \pi}
जब R \rightarrow \infty, \rho_1 \rightarrow 0, \rho_2 \rightarrow 0 , (1) से हम रखते हैं:
\int_{-\infty}^{\infty} f(x) d x-i \pi+\int_0^{\infty} f(x) d x+\int_{\infty}^{\infty} f(x+i \pi) d x +i \pi e^{-\alpha \pi}+\int_0^{-\infty} f(x+i \pi) d x=0 \\ \Rightarrow \int_{-\infty}^{\infty} \frac{e^{i \alpha x}}{\sinh x} d x-\int_{-\infty}^{\infty} \frac{e^{i \alpha(x+i \pi)}}{\sinh (x+i \pi)} d x=i \pi\left(1-e^{-\alpha \pi}\right) \\ \Rightarrow \int_{-\infty}^{\infty} \frac{e^{i \alpha x}}{\sinh x} d x+\int_{-\infty}^{\infty} \frac{e^{i \alpha x} e^{-\alpha \pi}}{\sinh x} d x=\pi i\left(1-e^{-\alpha \pi}\right) [\because \sinh (x+i \pi)=\sinh x \cos \pi+i \cosh x \sin \pi=-\sin x] \\ \Rightarrow \int_{-\infty}^{\infty} \frac{\left(1+e^{-\alpha \pi} \right)}{\sinh x} e^{i \alpha x} d x=i \pi\left(1-e^{-\alpha \pi}\right)
दोनों पक्षों के काल्पनिक भागों की तुलना करने परः
\int_{-\infty}^{\infty} \frac{\left(1+e^{-\alpha \pi}\right) \sin \alpha x}{\sinh x} d x=\pi\left(1-e^{-\alpha \pi}\right) \\ \Rightarrow 2 \int_0^{\infty} \frac{\sin \alpha x}{\sinh x} d x=\pi\left(\frac{e^{\alpha \pi}-1}{e^{\alpha \pi}+1}\right) \\ \Rightarrow \int_0^{\infty} \frac{\sin \alpha x}{\sinh x} d x=\frac{\pi}{2}\left(\frac{e^{\alpha \pi}-1}{e^{\alpha \pi}+1}\right)
उपर्युक्त उदाहरणों के द्वारा परिरेखा समाकलन द्वारा सिद्ध कीजिए (Prove that by Contour Integration),परिरेखा समाकलन (Contour Integration) को समझ सकते हैं।
Also Read This Article:- To Use Method of Contour Integration
3.परिरेखा समाकलन द्वारा सिद्ध कीजिए (Frequently Asked Questions Related to Prove that by Contour Integration),परिरेखा समाकलन (Contour Integration) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.परिरेखा का क्या अर्थ है? (What Does Contour Mean?):
उत्तर:यदि x(t) तथा y(t) जहाँ \alpha \leq t \leq \beta ,t के संतत फलन हों तो समीकरण
z=z(t)=x(t)+i y(t) …..(1)
सम्मिश्र तल में एक संतत चाप L को निरूपित करता है।
यदि उक्त समीकरण (1) में दिए हुए प्रान्त में t के एक से अधिक मान के लिए सन्तुष्ट हो तो बिन्दु z या (x,y) को चाप का बहुल बिन्दु (multiple point) कहते हैं।बिना बहुल बिन्दु वाले संतत चाप को जोरदाँ (Jordan) चाप कहते हैं।
परिमित संख्या में नियमित चापों के संतत श्रृंखला (chain) से बनने वाले जोरदाँ वक्र को कंटूर (contour) कहा जाता है।
प्रश्न:2.अनन्तकों पर अवशेषों का योग कैसे ज्ञात करते हैं? (How is the Sum of Residues on poles Determined?):
उत्तर: \int_0^{\infty} f(x) d x तथा \int_{-\infty}^{\infty} f(x) d x दोनों अभिसारी हैं,तो \int_{-\infty}^{\infty} f(x) dx= 2 \pi i \Sigma R^{+} यहाँ \Sigma R^{+} फलन f(z) के उपरि z-अर्धतल में स्थित अनन्तकों पर अवशेष का योग है।
प्रश्न:3.वृत्त का चतुर्थांश और आयत आदि परिरेखाओं के समाकलन के बारे में बताएं। (Describe the Integration of a Circle of Quadrant and Rectangle etc. with Contour):
उत्तर: \int_{-\infty}^{\infty} f(x) d x प्रकार के समाकलों का मूल्यांकन करने के लिए अन्य प्रकार की दन्तुरण सहित और दन्तुरण रहित परिरेखाओं जैसे वृत्त का चतुर्थांश,वृत्त खण्ड,आयत आदि का प्रयोग करते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा परिरेखा समाकलन द्वारा सिद्ध कीजिए (Prove that by Contour Integration),परिरेखा समाकलन (Contour Integration) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here | |
| 7. | click here |
Prove that by Contour Integration
परिरेखा समाकलन द्वारा सिद्ध कीजिए
(Prove that by Contour Integration)
Prove that by Contour Integration
परिरेखा समाकलन द्वारा सिद्ध कीजिए (Prove that by Contour Integration) के इस आर्टिकल
में ऐसे समाकलों का मान ज्ञात करना सीखेंगे जिन्हें वर्ग,आयत,वृत्त के चतुर्थांश आदि परिरेखा
का प्रयोग किया गया हो।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.