Vectors in Class 12
1.कक्षा 12 में सदिश (Vectors in Class 12),सदिश कक्षा 12 (Vectors Class 12):
कक्षा 12 में सदिश (Vectors in Class 12) के इस आर्टिकल में सदिशों के मात्रक सदिश व सदिश की दिक्कोसाइन ज्ञात करने से सम्बन्धित सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Vectors Class 12
2.कक्षा 12 में सदिश के उदाहरण (Vectors in Class 12 Illustrations):
Illustration:1.निम्नलिखित सदिशों के परिमाण का परिकलन कीजिए:
\vec{a}=\hat{i}+\hat{j}+\hat{k} ; \vec{b}=2 \hat{i}-7 \hat{j}-3 \hat{k} ; \vec{c}=\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}+\frac{1}{\sqrt{3}} \hat{k}
Solution:सदिश \vec{a} का परिमाण=|\vec{a}|\\ =|\hat{i}+\hat{j}+\hat{k}| \\ =\sqrt{(1)^2+(1)^2+(1)^2} \\ =\sqrt{1+1+1} \\ \Rightarrow|\vec{a}| =\sqrt{3}
सदिश \vec{b} का परिमाण=|\vec{b}| \\ =|2 \hat{i}-7 \hat{j}-3 \hat{k}| \\ =\sqrt{(2)^2+(-7)^2+(-3)^2} \\ =\sqrt{4+49+9} \\ =\sqrt{62} \\ \Rightarrow |\vec{b}|=\sqrt{62}
सदिश \vec{c} का परिमाण=|\vec{c}| \\ =\left|\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}-\frac{1}{\sqrt{3}} \hat{k}\right| \\ =\sqrt{\left(\frac{1}{\sqrt{3}}\right)^2+\left(\frac{1}{\sqrt{3}}\right)^2 +\left(-\frac{1}{\sqrt{3}}\right)^2} \\ =\sqrt{\frac{1}{3}+\frac{1}{3}+\frac{1}{3}} \\ =\sqrt{\frac{1+1+1}{3}} \\ \Rightarrow|\vec{c}|=1
अतः |\vec{a}|=\sqrt{3},|\vec{b}|=\sqrt{62},|\vec{c}|=1
Illustration:2.समान परिमाण वाले दो विभिन्न सदिश लिखिए।
Solution:माना \vec{a}=2 \hat{i}+3 \hat{j}-4 \hat{k}\\ \vec{b} =4 \hat{i}-2 \hat{j}+3 \hat{k} \\ |\vec{a}| =\sqrt{(2)^2+(3)^2+(-4)^2} \\ =\sqrt{4+9+16} \\ \Rightarrow |\vec{a}| =\sqrt{29} \\ |\vec{b}| =|4 \hat{i}-2 \hat{j}+3 \hat{k}| \\ =\sqrt{(4)^2+(-2)^2+(3)^2} \\ =\sqrt{16+4+9} \\ \Rightarrow |\vec{b}|=\sqrt{29}
अतः |\vec{a}|=|\vec{b}|
फलतः \vec{a} व \vec{b} भिन्न सदिश हैं जिनके परिमाण समान हैं।
Illustration:3.समान दिशा वाले दो विभिन्न सदिश लिखिए।
Solution:माना सदिश
\vec{a}=2 \hat{i}+3 \hat{j}+4 \hat{k} तथा \vec{b}=6 \hat{i}+9 \hat{j}+12 \hat{k}
सदिश \vec{a} के दिक्कोसाइन
l_1=\frac{2}{\sqrt{(2)^2+(3)^2+(4)^2}}=\frac{2}{\sqrt{4+9+16}}=\frac{2}{\sqrt{29}} \\ m_2=\frac{3}{\sqrt{(2)^2+(3)^2+(4)^2}}=\frac{3}{\sqrt{4+9+16}}=\frac{3}{\sqrt{29}} \\ n_2=\frac{4}{\sqrt{(2)^2+(3)^2+(4)^2}}=\frac{4}{\sqrt{4+9+16}}=\frac{4}{\sqrt{29}}
सदिश \vec{b} के दिक्कोसाइन
l_2=\frac{6}{\sqrt{(6)^2+(9)^2+(12)^2}}=\frac{6}{\sqrt{36+81+144}}=\frac{9}{\sqrt{261}}=\frac{2}{\sqrt{29}} \\ m_2=\frac{9}{\sqrt{(6)^2+(9)^2+(1)^2}}=\frac{9}{\sqrt{36+81+144}}=\frac{9}{\sqrt{261}} =\frac{3}{\sqrt{29}} \\ n_2=\frac{12}{\sqrt{(6)^2+(9)^2+(12)^2}}=\frac{12}{\sqrt{36+81+444}} =\frac{12}{\sqrt{261}}=\frac{4}{\sqrt{29}}
अतः दोनों सदिशों \vec{a} व \vec{b} की दिक्कोसाइन समान हैं अर्थात्
\frac{2}{\sqrt{29}}, \frac{3}{\sqrt{29}}, \frac{4}{\sqrt{29}}
परन्तु दोनों सदिशों का परिमाण भिन्न है:
|\vec{a}|=\sqrt{(2)^2+(3)^2+(4)^2}=\sqrt{4+9+16}=\sqrt{25} \\ |\vec{b}|=\sqrt{(6)^2+(9)^2+(12)^2}=\sqrt{36+81+144}=\sqrt{26} \\ \Rightarrow |\vec{a}| \neq |\vec{b}|
Illustration:4.x और y के मान ज्ञात कीजिए ताकि सदिश 2 \hat{i}+3 \hat{j} और x \hat{i}+y \hat{j} समान हों।
Solution: \vec{a}=\vec{b} \\ =2 \hat{i}+3 \hat{j}=x \hat{i}+y \hat{j}
तुलना करने परः
x=2,y=3
Illustration:5.एक सदिश का प्रारम्भिक बिन्दु (2,1) है और अन्तिम बिन्दु (-5,7) है।इस सदिश के अदिश और सदिश घटक ज्ञात कीजिए।
Solution:माना A(2,1) तथा B(-5,7) है तब \overrightarrow{A B} =\overrightarrow{O B}-\overrightarrow{O A} \\ =(-5 \hat{i}+7 \hat{j})-(2 \hat{i}+\hat{j}) \\ \Rightarrow \overrightarrow{A B} =-7 \hat{j}+6 \hat{j}
\therefore \overrightarrow{A B} के अदिश घटक -7 तथा 6 हैं।
तथा के सदिश घटक -7 \hat{j} तथा 6 \hat{j} हैं।
Illustration:6.सदिश \vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k} और \vec{z}=\hat{i}-6 \hat{j}-7 \hat{k} का योगफल ज्ञात कीजिए।
Solution:सदिशों \vec{a}, \vec{b} और \vec{c} का योगफल
=\vec{a}+\vec{b}+\vec{c} \\ =\hat{i}-2 \hat{j}+\hat{k}-2 \hat{i}+4 \hat{j}+5 \hat{k}+\hat{i}-6 \hat{j}-7 \hat{k} \\ \vec{a}+\vec{b}+\vec{c}=-4 \hat{j}-\hat{k}
Illustration:7.सदिश \vec{a}=\hat{i}+\hat{j}+2 \hat{k} के अनुदिश एक मात्रक सदिश ज्ञात कीजिए।
Solution: \vec{a}=\hat{i}+\hat{j}+2 \hat{k} \\ |\vec{a}|=\sqrt{(1)^2+(1)^2+(2)^2} =\sqrt{1+1+4}=\sqrt{6}
मात्रक सदिश \hat{a}=\frac{\vec{a}}{| \vec{a}|} \\ =\frac{\hat{i}+\hat{j}+2 \hat{k}}{\sqrt{6}} \\ \Rightarrow \hat{a}=\frac{1}{\sqrt{6}} \hat{i}+\frac{1}{\sqrt{6}} \hat{j}+\frac{2}{\sqrt{6}} \hat{k}
Illustration:8.सदिश के अनुदिश मात्रक सदिश ज्ञात कीजिए जहाँ बिन्दु P और Q क्रमशः (1,2,3) और (4,5,6) हैं।
Solution: \overrightarrow{PQ}=\overrightarrow{O Q}-\overrightarrow{OP} \\ =(4 \hat{i}+5 \hat{j}+6 \hat{k})-(\hat{i}+2 \hat{j}+3 \hat{k}) \\ \Rightarrow \overrightarrow{P Q}=3 \hat{i}+3 \hat{j}+3 \hat{k}
मात्रक सदिश
\widehat{PQ}=\frac{\overrightarrow{P Q}}{|\overrightarrow{P Q}|} \\ =\frac{3 \hat{i}+3 \hat{j}+3 \hat{k}}{\sqrt{(3)^2+(3)^2+(3)^2}} \\ =\frac{3(\hat{i}+\hat{j}+\hat{k})}{\sqrt{9+9+9}} \\ =\frac{3(\hat{i} +\hat{j}+\hat{k})}{\sqrt{27}} \\ =\frac{3(\hat{i}+\hat{j}+\hat{k})}{3 \sqrt{3}} \\ \Rightarrow \widehat{PQ} =\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}+\frac{1}{\sqrt{3}} \hat{k}
Illustration:9.दिए हुए सदिशों \vec{a}=2 \hat{i}-\hat{j}+2 \hat{k} और \vec{b}=-\hat{i}+\hat{j}-\hat{k} के लिए सदिश \vec{a}+\vec{b} के अनुदिश मात्रक सदिश ज्ञात कीजिए।
Solution: \vec{a}=2 \hat{i}-\hat{j}+2 \hat{k} तथा \vec{b}=-\hat{i}+\hat{j}-\hat{k} \\ \vec{a}+\vec{b}=(2 \hat{i}-\hat{j}+2 \hat{k})+(- \hat{i}+\hat{j}-\hat{k}) \\ \Rightarrow \vec{a}+\vec{b}= \hat{i}+ \hat{k} \\ |\vec{a}+\vec{b}|=|\hat{i}+\hat{k}| \\ =\sqrt{(1)^2+(0)^2+(1)^2} \\ =\sqrt{1+1} \\ |\vec{a}+\vec{b}|=\sqrt{2}
सदिश \vec{a}+\vec{b} के अनुदिश मात्रक सदिश = \frac{\vec{a}+\vec{b}}{|\vec{a}+\vec{b}|} \\ =\frac{\hat{i}+\hat{k}}{\sqrt{2}} \\ =\frac{1}{\sqrt{2}} \hat{i}+\frac{1}{\sqrt{2}} \hat{k}
Illustration:10.सदिश 5 \hat{i}-\hat{j}+2 \hat{k} के अनुदिश एक ऐसा सदिश ज्ञात कीजिए जिसका परिमाण 8 इकाई है।
Solution:माना \vec{a}=5 \hat{i}-\hat{j}+2 \hat{k} \\ |\vec{a}|=\sqrt{(5)^2+(-1)^2+(2)^2} \\ \Rightarrow |\vec{a}|=\sqrt{25+7+4}=\sqrt{30}
\vec{a} के अनुदिश एकांक सदिश \hat{a}=\frac{\vec{a}}{|\vec{a}|} \\ \hat{a}=\frac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}}
अतः \vec{a} के अनुदिश 8 परिमाण वाला सदिश =8 \hat{a} \\ =8\left(\frac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}}\right) \\ \Rightarrow 8 \hat{a} =\frac{50}{\sqrt{30}} \hat{i}-\frac{8}{\sqrt{30}} \hat{j}+\frac{16}{\sqrt{30}} \hat{k}
Illustration:11.दर्शाइए कि सदिश 2 \hat{i}-3 \hat{j}+4 \hat{k} और -4 \hat{i}+6 \hat{j}-8 \hat{k} संरेख हैं।
Solution:माना \vec{a}=2 \hat{i}-3 \hat{j}+4 \hat{k}
तथा \vec{b}=-4 \hat{i}+6 \hat{j}-8 \hat{k} \\ =-2(2 \hat{i}-3 \hat{j}+4 \hat{k}) \\ \Rightarrow \vec{b} =-2 \vec{a}
अतः सदिश \vec{a} को \vec{b} के रूप में और \vec{b} को \vec{a} के रूप में व्यक्त किया जा सकता है।फलतः सदिश \vec{a} व \vec{b} संरेख है।
Illustration:12.सदिश \hat{i}+2 \hat{j}+3 \hat{k} की दिक् cosine ज्ञात कीजिए।
Solution:माना \vec{r}=\hat{i}+2 \hat{j}+3 \hat{k}
के दिक् अनुपात हैं 1,2,3
\sqrt{a^2+b^2+c^2}=\sqrt{(1)^2+(2)^2+(3)^2}=\sqrt{14}
\therefore दिक्कोसाइन l= \pm \frac{a}{\sqrt{a^2+b^2+c^2}}= \pm \frac{1}{\sqrt{14}} \\ m=\pm \frac{ b}{\sqrt{a^2+b^2+c^2}}= \pm \frac{2}{\sqrt{14}}
तथा n=\pm \frac{ c}{\sqrt{a^2+b^2+c^2}}= \pm \frac{3}{\sqrt{14}}
अतः दिए गए सदिश के दिक्कोसाइन हैंः
\pm \frac{1}{\sqrt{14}}, \pm \frac{2}{\sqrt{14}}, \pm \frac{3}{\sqrt{14}}
Illustration:13.बिन्दुओं A(1,2,-3) एवं B(-1,-2,1) को मिलाने वाले एवं A से B की तरफ दिष्ट सदिश की दिक् cosine ज्ञात कीजिए।
Solution:A से B की तरफ दिष्ट सदिश =\overrightarrow{A B} \\ \overrightarrow{A B}=\left(x_2-x_1\right) \hat{i}+\left(y_2-y_1\right) \hat{j}+\left(z_2-z_1\right) \hat{k}
यहाँ \left(x_1, y_1, z_1\right)=(1,2,-3)
तथा \left(x_2, y_2, z_2\right)=(-1,-2,1) \\ \Rightarrow \overrightarrow{A B}=(-1-1) \hat{i}+(-2-2) \hat{j}+(1-(-3)) \hat{k} \\ \Rightarrow \overrightarrow{A B}=-2 \hat{i}-4 \hat{j}+4 \hat{k}
सदिश \overrightarrow{A B} के दिक् अनुपात a,b,c=-2,-4,4
\sqrt{a^2+b^2+c^2}=\sqrt{(-2)^2+(-4)^2+(4)^2} \\ =\sqrt{4+16+16} \\ =\sqrt{36} \\ \Rightarrow \sqrt{a^2+b^2+c^2}=6
अतः \overrightarrow{A B} के दिक्कोसाइन
l=\pm \frac{ a}{\sqrt{a^2+b^2+c^2}}= \pm \frac{(-2)}{6}=\mp \frac{1}{3} \\ m= \pm \frac{ b}{\sqrt{a^2+b^2+c^2}}= \pm \frac{(-4)}{6}=\mp \frac{2}{3} \\ n= \pm \frac{c}{\sqrt{a^2+b^2+c^2}}= \pm \frac{4}{6}= \pm \frac{2}{3}
अतः अभीष्ट दिक्कोसाइन हैंः
\mp \frac{1}{3}, \mp \frac{2}{3}, \pm \frac{2}{3}
Illustration:14.दर्शाइए कि सदिश \hat{i}+\hat{j}+\hat{k} अक्षों OX,OY एवं OZ के साथ बराबर झुका हुआ है।
Solution:माना \vec{r}=\hat{i}+\hat{j}+\hat{k}
\vec{r} के दिक् अनुपात a,b,c=1,1,1
\sqrt{a^2+b^2+c^2}=\sqrt{(1)^2+(1)^2+(1)^2}=\sqrt{3} \\ l= \pm \frac{a}{\sqrt{a^2+b^2+c^2}}, m= \pm \frac{b}{\sqrt{a^2+b^2+c^2}}, n= \pm \frac{c}{\sqrt{a^2+b^2+c^2}} \\ \Rightarrow l= \pm \frac{1}{\sqrt{3}}, \quad m= \pm \frac{1}{\sqrt{3}}, n= \pm \frac{1}{\sqrt{3}} \\ \Rightarrow l=m=n= \pm \frac{1}{\sqrt{3}}
अतः सदिश अक्षों के साथ बराबर झुका हुआ है।
Illustration:15.बिन्दुओं P(\hat{i}+2 \hat{j}-\hat{k}) और Q(-\hat{i}+\hat{j}+\hat{k}) को मिलाने वाली रेखा को 2:1 के अनुपात में (i)अंतः (ii)बाह्य, विभाजित करने वाले बिन्दु R का स्थिति सदिश ज्ञात कीजिए।
Solution: \overrightarrow{OP}=\hat{i}+2 \hat{j}-\hat{k}
तथा \overrightarrow{OQ}=-\hat{i}+\hat{j}+\hat{k}
R,P व Q को मिलाने वाली रेखा को 2:1 में अन्तः विभाजित करता है तब
\overrightarrow{OR} =\frac{m(\overrightarrow{OQ})+n(\overrightarrow{OP})}{m+n} \\ =\frac{2(-\hat{i}+\hat{j}+\hat{k})+1(\hat{i}+2 \hat{j}-k)}{2+1} \\ =\frac{-2 \hat{i}+2 \hat{j}+2 \hat{k}+\hat{i}+2 \hat{j}-\hat{k}}{3} \\ \Rightarrow \overrightarrow{OR}=-\frac{1}{3} \hat{i}+\frac{4}{3} \hat{j}+\frac{1}{3} \hat{k}
R,P तथा Q को मिलाने वाली रेखा को 2:1 के अनुपात में बाह्य विभाजित करता है,तब
\overrightarrow{OR}=\frac{m(\overrightarrow{OQ})-n(\overrightarrow{O P})}{m-n} \\ =\frac{2(-\hat{i}+\hat{j}+\hat{k})-1(\hat{i}+2 \hat{j}-k)}{2-1} \\ =\frac{-2 \hat{i}+2 \hat{j}+2 \hat{k}-\hat{i}-2 \hat{j}+\hat{k}}{1} \\ \Rightarrow \overrightarrow{OR}=-3 \hat{i}+3 \hat{k}
Illustration:16.दो बिन्दुओं P(2,3,4) और Q (4,1,-2) को मिलाने वाले सदिश का मध्य बिन्दु ज्ञात कीजिए।
Solution: \overrightarrow{O P}=2 \hat{i}+3 \hat{j}+4 \hat{k}
तथा \overrightarrow{OQ}=4 \hat{i}+\hat{j}-2 \hat{k}
मध्य बिन्दु R का स्थिति सदिश
\overrightarrow{O R} =\frac{\overrightarrow{OP}+\overrightarrow{O Q}}{2} \\ =\frac{2 \hat{i}+3 \hat{j}+4 \hat{k} +4 \hat{i}+ \hat{j}-2 \hat{k}}{2} \\ \Rightarrow \overrightarrow{O R}=\frac{6 \hat{i}+4 \hat{j}+2 \hat{k}}{2} \\ \Rightarrow \overrightarrow{O R} =3 \hat{i}+2 \hat{j}+\hat{k}
Illustration:17.दर्शाइए कि बिन्दु A,B और C,जिनके स्थिति क्रमशः \vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}, \vec{b}=2 \hat{i}-\hat{j}+\hat{k} और \vec{c}=\hat{i}-3 \hat{j}-5 \hat{k} हैं,एक समकोण त्रिभुज के शीर्षों का निर्माण करते हैं।
Solution:प्रश्नानुसार \overrightarrow{O A}=\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k} \\ \overrightarrow{O B}=\vec{B}=2 \hat{i}-\hat{j}+\hat{k}, \overrightarrow{O C}=\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k} \\ \overrightarrow{A B}=\overrightarrow{O B}-\overrightarrow{OA}=(2 \hat{i}-\hat{j}+\hat{k})-(3 \hat{i}-4 \hat{j}-4 \hat{k}) \\ =2 \hat{i}-\hat{j}+\hat{k}-3 \hat{i}+4 \hat{j}+4 \hat{k} \\ \Rightarrow \overrightarrow{A B}=-\hat{i}+3 \hat{j}+5 \hat{k} \\ \overrightarrow{A B}=\sqrt{(-1)^2+(3)^2+(5)^2} \\ =\sqrt{1+9+25} \\ \Rightarrow |\overrightarrow{A B}|=\sqrt{35} \\ \overrightarrow{B C}=\overrightarrow{OC}-\overrightarrow{OB} =(\hat{i}-3 \hat{j}-5 \hat{k})-(2 \hat{i}-\hat{j}+\hat{k}) \\ =\hat{i}-3 \hat{j}-5 \hat{k}-2 \hat{i}+\hat{j}-\hat{k} \\ \Rightarrow \overrightarrow{B C}=-\hat{i}-2 \hat{j}-6 \hat{k} \\ |\overrightarrow{B C}| =\sqrt{(-1)^2+(-2)^2+(-6)^2} \\ =\sqrt{1+4+36} \\ \Rightarrow |\overrightarrow{B C}|=\sqrt{41} \\ \overrightarrow{C A}=\overrightarrow{O A}-\overrightarrow{O C}=(3 \hat{i}-4 \hat{j}-4 \hat{k})-(\hat{i}-3 \hat{j}-5 \hat{k}) \\ = 3 \hat{i}-4 \hat{j}-4 \hat{k}-\hat{i}+3 \hat{j}+5 \hat{k} \\ \Rightarrow \overrightarrow{C A}=2 \hat{i}-\hat{j}+\hat{k} \\ \Rightarrow |\overrightarrow{C A}|=|2 \hat{i}-\hat{j}+\hat{k}| \\ =\sqrt{(2)^2+(-1)^2+(1)^2} \\ =\sqrt{4+1+1} \\ \Rightarrow |\overrightarrow{C A}| =\sqrt{6} \\ |\overrightarrow{A B}|^2+|\overrightarrow{C A}|^2=(\sqrt{35})^2+(\sqrt{6})^2 \\ =35+6 \\ =41 \\ \Rightarrow|\overrightarrow{A B}|^2+|\overrightarrow{C A}|^2=|\overrightarrow{B C}|^2
अतः \triangle A B C एक समकोण त्रिभुज है।
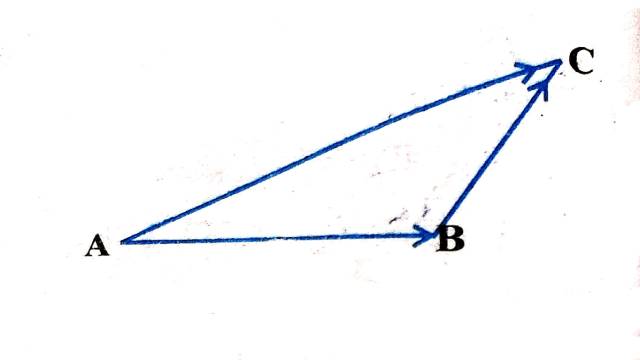
Illustration:18.त्रिभुज ABC (आकृति 10.18) के लिए निम्नलिखित में से कौन सा कथन सत्य नहीं है।
(A) \overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}=\overrightarrow{0}
(B) \overrightarrow{A B}+\overrightarrow{B C}-\overrightarrow{A C}=\overrightarrow{0}
(C) \overrightarrow{A B}+\overrightarrow{B C}-\overrightarrow{C A}=\overrightarrow{0}
(D) \overrightarrow{A B}-\overrightarrow{C B}+\overrightarrow{C A}=\overrightarrow{0}
Solution:सदिशों के योगफल त्रिभुज नियम के अनुसार
\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C} \\ \Rightarrow \overrightarrow{A B}+\overrightarrow{B C}-\overrightarrow{A C}=0 \\ \Rightarrow \overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}=0
अतः कथन (C) सत्य नहीं है फलतः विकल्प (C) उत्तर होगा।
Illustration:19.यदि \vec{a} और \vec{b} दो संरेख सदिश हैं तो निम्नलिखित में से कौन सा कथन सही नहीं है।
(A)\vec{b}=\lambda \vec{a},किसी अदिश \lambda के लिए
(B) \vec{a}= \pm \vec{b}
(C) \vec{a} और \vec{b} के क्रमागत घटक समानुपाती हैं।
(D)दोनों सदिशों \vec{a} तथा \vec{b} की दिशा समान है परन्तु परिमाण विभिन्न हैं।
Solution:संरेख सदिश आपस में समान्तर होते हैं परन्तु यह आवश्यक नहीं है कि उनकी दिशा और परिमाण समान हो।
अतः विकल्प (D) सही नहीं है।फलतः विकल्प (D) उत्तर होगा।
उपर्युक्त उदाहरणों के द्वारा कक्षा 12 में सदिश (Vectors in Class 12),सदिश कक्षा 12 (Vectors Class 12) को समझ सकते हैं।
3.कक्षा 12 में सदिश के सवाल (Vectors in Class 12 Questions):
(1.)त्रिभुज ABC की भुजाओं BC,CA और AB के मध्य बिन्दु क्रमशः D,E और F है,तो सिद्ध कीजिए कि
\overrightarrow{A D}+\overrightarrow{B E}+\overrightarrow{C F}=\overrightarrow{0}
(2.)सिद्ध कीजिए कि किसी त्रिभुज में किन्हीं दो भुजाओं के मध्य बिन्दुओं को मिलाने वाली रेखा,तीसरी भुजा के समान्तर और उसकी आधी होती है।
उपर्युक्त सवालों को हल करने पर कक्षा 12 में सदिश (Vectors in Class 12),सदिश कक्षा 12 (Vectors Class 12) को ठीक से समझ सकते हैं।
4.दो बिन्दुओं को मिलाने वाला सदिश (Vector joining two points):
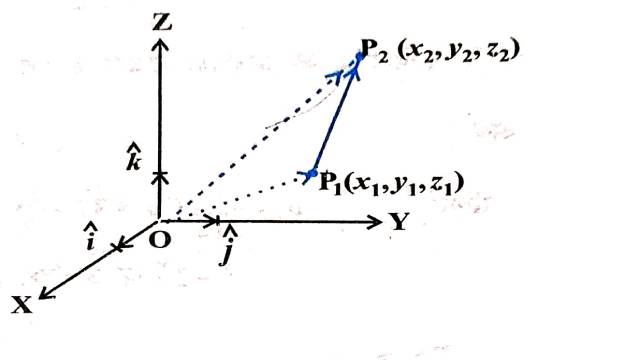
यदि P_1\left(x_1, y_1, z_1\right) और P_2\left(x_2, y_2, z_2\right) दो बिन्दु हैं तब P_1 को P_2 से मिलाने वाला सदिश है (आकृति)। P_1 और P_2 को मूल बिन्दु O से मिलाने पर और त्रिभुज नियम का प्रयोग करने पर हम त्रिभुज O P_1 P_2 से पाते हैं कि \overrightarrow{O P_1}+\overrightarrow{P_1 P_2}=\overrightarrow{O P_2} सदिश योगफल के गुणधर्मों का उपयोग करते हुए उपर्युक्त समीकरण निम्नलिखित रूप से लिखा जाता है:
\overrightarrow{P_1 P_2}=\overrightarrow{O P_2}-\overrightarrow{O P_1} \\ \Rightarrow \overrightarrow{P_1 P_2}=\left(x_2 \hat{i}+y_2\hat{j}+z_2 \hat{k}\right)-\left(x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}\right) \\ \Rightarrow \overrightarrow{P_1 P_2}=\left(x_2-x_1\right) \hat{i}+\left(y_2-y_1\right) \hat{j}+\left(z_2-z_1\right) \hat{k}
सदिश \overrightarrow{P_1 P_2} का परिमाण
\left| \overrightarrow{P_1 P_2}\right|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}
Also Read This Article:- Differential Equations in Class 12
5.कक्षा 12 में सदिश (Frequently Asked Questions Related to Vectors in Class 12),सदिश कक्षा 12 (Vectors Class 12) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.सदिश योग का त्रिभुज नियम क्या है? (What is the Triangle Law of Addition of Vectors?):
उत्तर:यदि दो सदिश परिमाण तथा दिशा में किसी त्रिभुज की दो क्रमवार भुजाओं से निरूपित किया जा सके तो इन सदिशों का योग,परिमाण व दिशा में,त्रिभुज की तीसरी भुजा द्वारा विपरीत क्रम में निरूपित होगा।
प्रश्न:2.सदिश योग का समान्तर चतुर्भुज नियम क्या है? (What is the Parallelogram Law of Addition of Vectors?):
उत्तर:यदि दो सदिश तथा परिमाण तथा दिशा में समान्तर चतुर्भुज की दो संलग्न (adjacent) भुजाओं द्वारा निरूपित होते हों तो उनका योग,परिमाण व दिशा में,सहप्रारम्भिक बिन्दु से गुजरने वाले विकर्ण द्वारा निरूपित होगा।
प्रश्न:3.मात्रक सदिश ज्ञात करने का सूत्र लिखो। (Write the Formula for Finding the Unit Vector):
उत्तर:सदिश का मात्रक सदिश निम्न प्रकार ज्ञात करते हैं:
\hat{a}=\frac{1}{|\hat{a}|} \vec{a}
उपर्युक्त प्रश्नों के उत्तर द्वारा कक्षा 12 में सदिश (Vectors in Class 12),सदिश कक्षा 12 (Vectors Class 12) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here | |
| 7. | click here |
Vectors in Class 12
कक्षा 12 में सदिश (Vectors in Class 12)
Vectors in Class 12
कक्षा 12 में सदिश (Vectors in Class 12) के इस आर्टिकल में सदिशों के मात्रक सदिश व
सदिश की दिक्कोसाइन ज्ञात करने से सम्बन्धित सवालों को हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.