Vertical Motion Under Gravity
1.गुरुत्वाकर्षण के अधीन उर्ध्वाधर गति (Vertical Motion Under Gravity),वेग के वर्ग-समानुपाती प्रतिरोध के अधीन एक कण की उर्ध्वाधर गति (Vertical Motion of a Particle Under Resistance Varies as Square of Velocity):
गुरुत्वाकर्षण के अधीन उर्ध्वाधर गति (Vertical Motion Under Gravity) कर रहे कण पर आधारित सवालों को हल करके गुरुत्वाकर्षण के अधीन कण एक ऐसे माध्यम में होकर गिरता है जिसका प्रतिरोध उसके वेग के वर्ग के समानुपाती है,समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Motion in Resisting Medium
2.गुरुत्वाकर्षण के अधीन उर्ध्वाधर गति पर आधारित उदाहरण (Illustration Based on Vertical Motion Under Gravity):
Illustration:1.एक कण को गुरुत्वाकर्षण के तहत प्रक्षेपित किया जाता है,हवा का प्रतिरोध वेग के विपरीत एक त्वरण उत्पन्न करता है और संख्यात्मक रूप से kv^2 के बराबर होता है,जहाँ v वेग है और k एक स्थिरांक है।यदि प्रारम्भिक वेग V है और \frac{k V^2}{g} का वर्ग उपेक्षित हो सकता है,तो दिखाएं कि कण अपनी उच्चतम ऊँचाई तक समय \frac{V}{g}-\frac{k V^2}{3 g^2} में पहुँचता है तथा उच्चतम लम्ब \frac{V^2}{2 g}-\frac{k V^4}{4 g^2} है
यदि प्रारम्भिक वेग,उर्ध्वाधर घटक V के अलावा,एक छोटा क्षैतिज घटक U है और प्रतिरोध उसी नियम का पालन करता है,तो दिखाएं कि जब कण मूल स्तर पर लौटता है तो इसका क्षैतिज वेग लगभग होता है:
v e^{-\frac{k v^2}{g}}
(A particle is projected vertically upwards under gravity.The resistance of the air produces an acceleration opposite of the velocity and numerically equal to kv^2 ,where v is the velocity and k a constant.If the initial velocity is V and the square of \frac{k V^2}{g} can be neglected,show that the particle reaches its highest point in time \frac{V}{g}-\frac{k V^2}{3 g^2} and that the greatest altitude reached is
\frac{V^2}{2 g}-\frac{k V^4}{4 g^2}
If the initial velocity,in addition to the vertical component V,has a small horizontal component V,and the resistance follows the same law,show that when the particle returns to the original level,its horizontal velocity is approximately v e^{-\frac{k v^2}{g}} .)
Solution:प्रतिरोध=k v^2
ऊपर की ओर गति का समीकरण
v \frac{d v}{d x}=-g-k v^2 \\ =-k\left(\frac{g}{k}+v^2\right) \cdots(1) \\ \Rightarrow \frac{2 v d v}{\frac{g}{k}+v^2}=-2 k d x
समाकलन करने पर:
\log \left(\frac{g}{k}+v^2\right)=-2 k x+C
प्रारम्भ में v=V,x=0 \therefore C=\log \left(\frac{g}{k}+V^2\right) \\ \therefore \log \left(\frac{g}{k}+v^2 \right)=-2 k x+\log \left(\frac{g}{k}+V^2\right) \\ \Rightarrow 2 k x=\log \left(\frac{\frac{g}{k}+V^2}{\frac{g}{k}+v^2}\right) \cdots(2)
उच्चतम बिन्दु पर v=0,माना x=h तब समीकरण (2) से
2kh=\log \left(\frac{\frac{g}{K}+V^2}{\frac{g}{K}}\right) \\ =\log \left(1+\frac{k}{g} V^2\right) \\ =\frac{k}{g} V^2-\frac{1}{2} \frac{k^2 V^4}{g^2}
[ \log \left(1+\frac{k}{g} V^2\right) का विस्तार करने पर:]
\Rightarrow h=\frac{v^2}{2 g}-\frac{k V^4}{4 g^2}
कण द्वारा समीकरण उच्चतम लम्ब (ऊँचाई) तक पहुँचने का समीकरण देती है।
समीकरण (1) को लिखा जा सकता है:
\frac{d v}{d t}=-k\left(\frac{g}{k}+v^2\right) \\ \Rightarrow \frac{d v}{\frac{g}{k}+v^2}=-k d t
समाकलन करने पर:
\frac{1}{\sqrt{\frac{g}{k}}} \tan^{-1} \left(v \sqrt{\frac{k}{g}}\right)=-k t+D \cdots(3)
प्रारम्भ में जब t=0,v=V
\therefore D=\frac{1}{\sqrt{\frac{g}{k}}} \tan ^{-1}\left(V \sqrt{\frac{k}{g}}\right)
अतः समीकरण (3) से:
t=\frac{1}{\sqrt{k g}}\left[\tan ^{-1}\left(V \sqrt{\frac{k}{g}}\right)-\tan ^{-1}\left(v \sqrt{\frac{k}{g}}\right)\right] \cdots(4)
यदि उच्चतम लम्ब तक पहुँचने में लगा समय t’ है तब समीकरण (4) में v=0 तथा t=t’ रखने पर:
t^{\prime}=\frac{1}{\sqrt{k g}} \tan ^{-1}\left(V \sqrt{\frac{k}{g}}\right) \\ =\frac{1}{\sqrt{k g}} \left[\sqrt{\left(\frac{k}{g}\right)} V-\frac{1}{3}\left(\frac{k}{g}\right)^{\frac{3}{2}} V^3+\cdots\right] \\ =\frac{V}{g}-\frac{k V^3}{3 g^2}
( \frac{k V^2}{g} का वर्ग तथा उच्चतम घातों की उपेक्षा करने पर)
जो कि अभीष्ट समय है।
अब जब क्षैतिज वेग V है,तब समय t में क्षैतिज तय की गई दूरी y है।क्षैतिज दिशा में गति का समीकरण:
\frac{d^2 y}{d t^2}=-k v^2 \cos \psi \\ \frac{d^2 y}{d t^2}=-k\left(\frac{d s}{d t}\right)^2 \frac{d y}{d s}\left[\because V=\frac{d s}{d t} \text{ तथा } \cos \psi=\frac{d y}{d s}\right] \\ =-k \frac{d s}{d t} \cdot \frac{d y}{d t} \\ \Rightarrow \frac{\frac{d^2 y}{d t^2}}{\frac{d y}{d t}}=-k \frac{d s}{d t}
समाकलन करने पर:
\log \left(\frac{d y}{d t}\right)=-k s+A
समाकलन करने पर:
प्रारम्भ में जब s=0 , \frac{d y}{d t}=V \therefore A=\log U \\ \therefore \log \left(\frac{d y}{d t}\right)=-k s+\log U \\ \Rightarrow \frac{d y}{d t}=U e^{-k s} \cdots(5)
U छोटा है और प्रतिरोधी माध्यम के कारण घटेगा तथा क्षैतिज तय की गई दूरी बहुत कम है तथा उर्ध्वाधर गति की तुलना में उपेक्षा कर सकते हैं।अतः उच्चतम लम्ब का दुगुना लगभग s ले सकते हैं जब कण पुनः तल पर पहुँचता है:
ks=2k (greatest altitude I.e. h)
=2kh \\ =\frac{k}{g} V^2-\frac{1}{2} \frac{k^2 V^4}{g^2} (h का मान रखने पर)
समीकरण (5) से:
\frac{d y}{d t}=u e^{-\frac{k V^2}{g}}
यह वेग का क्षैतिज घटक है।
Illustration:2.द्रव्यमान m का एक कण पृथ्वी के केन्द्र से a दूरी पर विरामावस्था से गिरता है,गति v वेग के वर्ग के आनुपातिक एक छोटे प्रतिरोध के साथ मिलती है और इकाई वेग के लिए मंदता \mu होती है,दिखाएँ कि केन्द्र से x दूरी पर गतिज ऊर्जा है।
m g r^2 \left[\frac{1}{x}-\frac{1}{a}+2 \mu\left(1-\frac{x}{a}\right)-2 \mu \log \left(\frac{a}{x}\right)\right] \\ \mu के वर्ग की उपेक्षा कर दी जाती है तथा r पृथ्वी की त्रिज्या है।
(A particle of mass m falls from rest at a distance a from the centre of the earth,the motion meeting a small resistance proportional to the square of the velocity v and the retardation being \mu for unit velocity,show that the kinetic energy at a distance x from the centre is
m g r^2 \left[\frac{1}{x}-\frac{1}{a}+2 \mu\left(1-\frac{x}{a}\right)-2 \mu \log \left(\frac{a}{x}\right)\right] \\ \mu the square of being neglected and r is the radius of the earth.)
Solution:माना पृथ्वी का केन्द्र O,जो निश्चित बिन्दु है।अतः कण O की ओर गिर रहा है।माना किसी क्षण कण की स्थिति P, O से x दूरी पर है।P पर कण पर निम्नलिखित बल कार्यरत हैं:
(1) \frac{\lambda}{x^2} आकर्षण पृथ्वी के केन्द्र की ओर अर्थात् x घटने की ओर
(3)माध्यम का प्रतिरोध \mu v^2 , O से दूर अर्थात् x बढ़ने की ओर।
अतः कण की गति का समीकरण:
v \frac{d v}{d x}=\mu v^2-\frac{\lambda}{x^2} \cdots(1)
पृथ्वी के तल पर गुरुत्वाकर्षण के कारण त्वरण g होगा:
g=\frac{\lambda}{r^2} \quad[\because x=r] \\ \Rightarrow \lambda=g r^2 \cdots(2)
(1) व (2) से:
v \frac{d v}{d x}=\mu v^2-\frac{g r^2}{x^2} \\ \Rightarrow \frac{1}{2} \frac{d v^2}{d x}-\mu v^2=-\frac{g r^2}{x^2} \\ \Rightarrow \frac{d v^2}{d x}-2 \mu v^2=-\frac{2 g r^2}{x^2} \cdots(3)
यह v^2 में रैखिक अवकल समीकरण है अतः
समाकलन गुणक (I.F.)=e^{\int -2 \mu d x}=e^{-2 \mu x}
(3) के दोनों पक्षों को e^{-2 \mu x} से गुणा करके समाकलन करने पर:
v^2 e^{-2 \mu x}=-2 g r^2 \int \frac{1}{x^2} e^{-2 \mu x} d x+C \\ \Rightarrow v^2(1-2 \mu x)=-2 g r^2 \int \frac{1}{x^2} (1-2 \mu x) d x+C
[ e^{-2 \mu x} का विस्तार करने एवं \mu की उच्चतम घातों को नगण्य मानने पर]
\Rightarrow v^2(1-2 \mu x)=-2 g r^2 \int \left[\frac{1}{x^2}-\frac{2 \mu}{x}\right] d x+C \\ =-2 g r^2\left[-\frac{1}{x}-2 \mu \log u\right]+C \cdots(4)
प्रारम्भ में जब x=0 तो v=0
\therefore C= 2 g r^2\left(-\frac{1}{a}-2 \mu \log a\right) \\ \therefore v^2(1-2 \mu x)=2 g r^2 \left(\frac{1}{x} +2 \mu \log x\right)+2 g r^2\left(-\frac{1}{a}-2 \mu \log a\right) \\ =2 g r^2\left[\frac{1}{x}-\frac{1}{a}-2 \mu \log \frac{a}{x}\right] \\ \Rightarrow v^2= 2 g r^2\left[\frac{1}{x}-\frac{1}{a} \cdot 2 \mu \log \frac{a}{x}\right](1-2 \mu x)^{-1} \\ =2g r^2\left[\frac{1}{x}-\frac{1}{a}-2 \mu \log \frac{a}{x}\right](1+2 \mu x+\cdots) \\ =2gr^2\left[\frac{1}{x}-\frac{1}{a}+\left(\frac{1}{x}-\frac{1}{a}\right) 2\ mu x-2 \mu \log \frac{a}{x}\right]
[ \mu का वर्ग और उच्चतम घातों को नगण्य मानने पर]
O (पृथ्वी के केन्द्र) से x दूरी पर कण की गतिज ऊर्जा =\frac{1}{2} m v^2 \\ =m g r^2\left[\frac{1}{x}-\frac{1}{a}+2 \mu x\left(\frac{1}{x}-\frac{1}{a}\right)-2 \mu \log \frac{a}{x}\right] \\ =m g r^2\left[\frac{1}{x}-\frac{1}{a}+2 \mu \left(1-\frac{x}{a}\right)-2 \mu \log \frac{a}{x}\right]
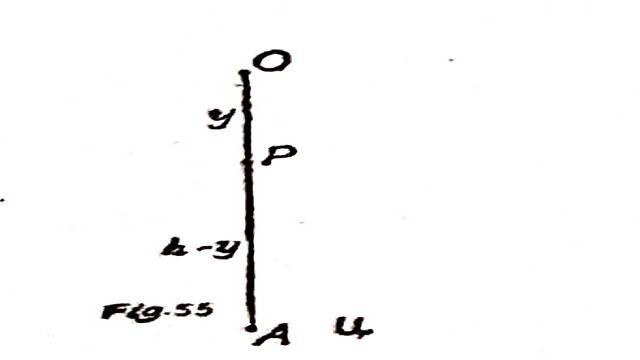
Illustration:3.किसी माध्यम में चलने वाले दो कण वेग के वर्ग के अनुसार गति करते हैं।एक को h ऊँचाई से गिरने दिया जाता है और दूसरे को उसी क्षण ऊपर की ओर प्रक्षेपित किया जाता है जिसका प्रारम्भिक वेग h ऊँचाई तक ले जाने के लिए पर्याप्त होता है।दर्शाइए कि कण \cos h \cdot \cos (\alpha-\beta)=1 द्वारा दिए गए उच्चतम बिन्दु के नीचे y की गहराई पर मिलते हैं जहाँ gy=V^2 \log \cosh \beta तथा g h=V^2 \sec \alpha ,V टर्मिनल वेग है।
(Two particles move in a medium whose resistance varies as square of the velocity.One is let fall from a height h and the other projected upwards at the same instant with initial velocity sufficient to carry it to a height h.Show that the particles meet at a depth y below the heightest point given by \cos h \cdot \cos (\alpha-\beta)=1 where gy=V^2 \log \cosh \beta and g h=V^2 \sec \alpha , V being the terminal velocity)
Solution:माना कि O से नीचे y गहराई पर t समय पश्चात P बिन्दु पर मिलते हैं तब
(प्रतिरोध वेग के वर्ग समानुपाती वाले सूत्र से)
\therefore gy=V^2 \log \cosh \beta जहाँ \beta=\frac{g}{v} t
पुनः यदि कण u वेग से प्रक्षेपित किया जाता है,तब
\frac{2 g}{V^2} x=\log \frac{V^2+u^2}{V^2+v^2} \cdots(2)
(प्रतिरोध वेग के वर्ग-समानुपाती सूत्र से)
उच्चतम ऊँचाई h है तब v=0 तथा x=h
\therefore \frac{2 g}{V^2} h=\log \frac{V^2+u^2}{V^2} \\ =\log \left(1+\frac{u^2}{V^2}\right) \cdots(3)
यदि \frac{u}{V}=\tan \alpha तब
\frac{2 g}{V^2} \cdot h =\log \left(1+\tan ^2 \alpha\right) \\ =\log \sec ^2 \alpha \\ =2 \log \sec \alpha \\ \therefore g h=V^2 \log \sec \alpha \cdots(4)
यदि P पर किसी समय t पर वेग v है जहाँ x=OP=h-y, तब (यह समय t समीकरण (1) से वही है प्रक्षेपित किया जाता है जबकि दूसरा कण उसी समय गिरता है)
t=\frac{V}{g}\left(\tan ^{-1} \frac{u}{V}-\tan ^{-1} \frac{v}{V}\right)
तथा \therefore \frac{2 g}{V^2}(h-y)=\log \frac{V^2+u^2}{V^2+v^2} [(2) से]…….(5)
\therefore \frac{2 g h}{V^2}-\frac{2 g}{V^2} y=\log \left(1+\frac{u^2}{V^2}\right)-\log \left(1+ \frac{v^2}{V^2}\right) \\ \Rightarrow \frac{2 g}{V^2} y=\log \left(1+\frac{v^2}{V^2}\right) [(3) से]
\Rightarrow 2 \log \cosh \beta=\log \left(1+\frac{v^2}{V^2}\right) [(1) से]
\Rightarrow \cosh ^2 \beta=1+\frac{v^2}{V^2} \\ \Rightarrow \cosh \beta-1=\frac{v^2}{V^2} \\ \Rightarrow \sinh \beta=\frac{v}{V} \cdots(6) \\ \frac{g t}{V}\left(\tan ^{-1} \frac{u}{V}-\tan ^{-1} \frac{v}{V}\right) [(5) से]
\beta=\tan ^{-1}(\tan \alpha)-\tan ^{-1}(\sinh \beta) [(1) व (6) से]
\Rightarrow \tan ^{-1}(\sinh \beta)=\alpha-\beta \\ \Rightarrow \sinh \beta=\tan (\alpha-\beta) \\ \Rightarrow \cos (\alpha-\beta)=\frac{1}{\sqrt{(1+\tan^2 (\alpha-\beta))}} \\ =\frac{1}{\sqrt{1+\sinh ^2 \beta}} \\ =\frac{1}{\cosh \beta} \\ \therefore \cosh \beta \cos (\alpha-\beta)=1 \cdots(7)
(1),(4),(7) से अभीष्ट परिणाम सिद्ध हुआ।
Illustration:4.एक कण को एक माध्यम में प्रक्षेपित किया जाता है जिसका प्रतिरोध g \frac{v}{V} है जहाँ वेग v है।यदि V प्रक्षेप वेग u की तुलना में बड़ा है,उर्ध्वाधर ऊँचाई तक पहुँच गया,चढ़ाई का समय और नीचे गिरने का समय उनके मूल्यों के भिन्न \frac{2 u}{3 V}, \frac{1}{2} \frac{u}{V} तथा \frac{1}{6} \frac{u}{V} लिया जाता है जब कोई प्रतिरोध नहीं होता है तथा कण प्रक्षेप बिन्दु पर वेग u\left(1-\frac{2}{3} \frac{u}{V}\right) से लौटता है।
(A particle is projected in a medium whose resistance is g \frac{v}{V} where v is the velocity.If V be large compared to u the velocity of projection, the vertical height reached, the time of ascent and the time of descent are described respectively by fraction \frac{2 u}{3 V}, \frac{1}{2} \frac{u}{V} and \frac{1}{6} \frac{u}{V} of their values when there is no resistance and that the particle returns to the point of projection with velocity u\left(1-\frac{2}{3} \frac{u}{V}\right)
Solution:प्रतिरोध=g \frac{v}{V}
गति का समीकरण
\frac{d^2 x}{d t^2}=-g-g \frac{v}{V}=-g\left(1+\frac{v}{V}\right) \\ \Rightarrow v \frac{d v}{d x}=-\frac{g}{V}(V+v) \cdots(1) \\ \int \frac{v+V-V}{V+v} d v=\int-\frac{g}{V} d x \\ \Rightarrow v-V \log (V+v)=-\frac{g}{V} x+A
जब x=0,v=u (दिया है)
\therefore u-V \log (V+u)=A \\ \therefore v-V \log (V+v)=-\frac{g}{V} x+u-V \log (V+u) \\ \therefore \frac{g}{V} x=u-v+V \log \frac{V+v}{V+u}
उच्चतम ऊँचाई पर x=h,v=0
\therefore \frac{g}{V} h=u+V \log \frac{V}{V+u}=1 \\ h=\frac{V u}{g}+\frac{V^2}{g} \log \frac{V}{V+u} \cdots(2)
उच्चतम ऊँचाई तक समय ज्ञात करने के लिए गति का समीकरण
\frac{d v}{d t}=-\frac{g}{V}(V+v) \\ \Rightarrow \int \frac{d v}{V+v}=-\int \frac{g}{V} d t \\ \log (V+v)=-\frac{g}{V} t+B
जब t=0,v=u \therefore B=\log (V+u) \\ \therefore \log \left(\frac{V+v}{V+u}\right)=-\frac{g}{V} t_1 \\ \log \frac{V}{V+u}=-\frac{g}{V} t_1 \\ \Rightarrow t_1 =-\frac{V}{g} \log \frac{V}{V+u} \cdots(3) \\ =\frac{V}{g} \log \left(\frac{V+u}{V}\right) \\ =\frac{V}{g} \log \left(1+\frac{u}{V}\right) \\ =\frac{V}{g} \left(\frac{u}{V}-\frac{u^2}{2 V^2}+\cdots\right) \\ \frac{u}{V} उच्चतम ऊँचाई पर v=0 तथा समय t_1 लिया हो तो
की उच्चतम घातों को नगण्य मानने पर:
\Rightarrow t_1=\frac{u}{g}-\frac{u^2}{2 V g}
जब प्रतिरोध नहीं है तो कण द्वारा लिया गया समय T_1=T_2=\frac{u}{g}
उच्चतम ऊँचाई H=\frac{u^2}{2 g} \cdots(4)
अतः t_1=T_1-T_1 \cdot \frac{u}{2 V}
अतः समय में कमी=T_1-t_1 \\ =T_1-\left(T_1-T_1 \frac{u}{2 V}\right) \\ =T_1 \cdot \frac{u}{2 V}=\frac{u}{2 V} of the time when there is no resistance
h=greatest height
=\frac{V u}{g}+\frac{V^2}{g} \log \frac{V}{V+u} [(2) से]
=\frac{V u}{g}-\frac{V^2}{g} \log \frac{V+u}{V} \\ =\frac{V u}{g}-\frac{V^2}{g} \log \left(1+\frac{u}{V}\right) \\ =\frac{V u}{g}-\frac{V^2}{g}\left(\frac{u}{V}-\frac{1}{2} \frac{u^2}{V^2}+\frac{1}{3} \frac{u^3}{V^3}\right)
(उच्चतम घातों को नगण्य मानने पर)
=\frac{V u}{g}-\frac{V u}{g}+\frac{u^2}{2 g}-\frac{u^3}{3Vg} \\ \Rightarrow h=H-\frac{2}{3} \frac{u}{V} H [(4) से]
ऊँचाई में कमी=H-h \\ =H-\left(H-\frac{2}{3} \frac{u}{V} H\right) \\ =\frac{2}{3} \frac{u}{V} H \\ =\frac{2}{3} \frac{u}{V} of the height when there is no resistance
गिरते समय कण की गति का समीकरण
\frac{d^2 x}{d t^2}=g-g \frac{u}{V} \\ \Rightarrow \int \frac{d v}{d t}=\int \frac{g}{V}(V-v) \\ \Rightarrow -\log (V-v)=\frac{g}{V} t+D
(टाॅप पर) जब t=0,v=0 तो D=-\log V \\ \therefore \log V-\log (V-v)=\frac{g}{V} t \\ \Rightarrow \log \frac{V}{V-v}=\frac{g}{V} t
जब कण प्रक्षेप बिन्दु पर समय t_2 बाद वेग u\left(1-\frac{2}{3} \frac{u}{V}\right) से पहुँचता है तो
\log \frac{V}{V-u\left(1-\frac{2}{3} \frac{u}{V}\right)}=\frac{g}{V} t_2 \\ \Rightarrow t_2=\frac{V}{g} \log \left(\frac{V}{V-u+\frac{2}{3}} \frac{u^2}{V}\right) \\ =-\frac{V}{g}\left(\frac{V-u+\frac{2}{3} \frac{u^2}{V}}{V}\right) \\ =-\frac{V}{g} \log \left(1-\left(\frac{u}{V}-\frac{2}{3} \frac{u^2}{V^2}\right)\right) \\ = -\frac{V}{g}\left[-\left(\frac{u}{V}-\frac{2}{3} \frac{u^2}{V^2}\right)-\frac{1}{2}\left(\frac{u}{V}-\frac{2}{3} \frac{u^2}{V^2}\right)^2- \cdots\right]
उच्चतम घातों को नगण्य मानने पर:
=-\frac{V}{g}\left(\frac{-u}{V}+\frac{2}{3} \frac{u^2}{V^2}-\frac{1}{2} \frac{u^2}{V^2}\right) \\ =-\frac{V}{g}\left(-\frac{u}{V}+\frac{1}{6} \frac{u^2}{V^2}\right) \\ =\frac{u}{g}-\frac{1}{6} \frac{u^2}{V g} \\ =T_2-\frac{1}{6} \frac{u}{V} T_2
अतः समय में कमी=T_2-t_2 \\ =T_2-\left(T_2-\frac{1}{6} \frac{u}{V} T_2\right) \\ =\frac{1}{6} \cdot \frac{u}{V} T_2 \\ =\frac{1}{6} \cdot \frac{u}{V} of the time when there is no resistance
उपर्युक्त उदाहरणों के द्वारा गुरुत्वाकर्षण के अधीन उर्ध्वाधर गति (Vertical Motion Under Gravity),वेग के वर्ग-समानुपाती प्रतिरोध के अधीन एक कण की उर्ध्वाधर गति (Vertical Motion of a Particle Under Resistance Varies as Square of Velocity) को समझ सकते हैं।
Also Read This Article:- Theorem of Parallel Axes in Dynamics
3.गुरुत्वाकर्षण के अधीन उर्ध्वाधर गति (Frequently Asked Questions Related to Vertical Motion Under Gravity),वेग के वर्ग-समानुपाती प्रतिरोध के अधीन एक कण की उर्ध्वाधर गति (Vertical Motion of a Particle Under Resistance Varies as Square of Velocity) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.प्रतिरोधी माध्यम में सरल रेखीय गति के विभिन्न सूत्र लिखो। (Write All Formulas of Resistance of Rectilinear Motion in Resisting Medium):
उत्तर:(1.) कण को प्रतिरोधी माध्यम जिसका प्रतिरोध वेग के वर्गानुपाती गुरुत्वाकर्षण के अधीन u वेग से ऊपर फेंका जाता है
(i) \frac{d^2 x}{d t^2}=-\frac{g}{V^2}\left(V^2+v^2\right)
(ii) \frac{2 g}{V^2} x \log \left(\frac{V^2+u^2}{V^2+v^2}\right)
(iii) t=\frac{V}{g}\left(\tan^{-1} \frac{u}{V}-\tan ^{-1} \frac{v}{V}\right)
(2.)कण को प्रतिरोधी माध्यम जिसका प्रतिरोध वेग के वर्गानुपाती गुरुत्वाकर्षण के अधीन गिरता है
(i) \frac{d^2 x}{d t^2}=g\left(1-\frac{v^2}{V^2}\right)
(ii) v^2=V^2\left(1-e^{\left(-\frac{2 g}{V^2}\right) x}\right)
(iii) v=V \tanh \frac{g}{V} t
(iv) x=\frac{v^2}{g} \log \cosh \frac{g}{V} t
प्रश्न:2.प्रतिरोधी माध्यम जिसका प्रतिरोध वेग के वर्गानुपाती हो में कण का उड्डयन काल कैसे ज्ञात करते हैं? (How is the Time of Flight of a particle in a Resisting Medium Whose Resistance is Square to Velocity?):
उत्तर:प्रश्न 1(iii) के उत्तर में v=0,t=T रखने पर:
T=\frac{u}{g} \tan \frac{u}{V}
प्रश्न:3.प्रतिरोधी माध्यम जिसका प्रतिरोध वेग के वर्गानुपाती हो में कण द्वारा तय की गई अधिकतम ऊँचाई कैसे ज्ञात करते हैं? (How to Determine the Greatest Height Moved by the Particle in a Resisting Medium by the Particle Whose Resistance is Square to Velocity?):
उत्तर:अधिकतम ऊँचाई पर कण का वेग v=0 तथा x=H प्रश्न के उत्तर 1(ii) में रखने पर:
\frac{2 g H}{V^2}=\log \left(\frac{V^2+u^2}{V^2}\right) \\ \Rightarrow H=\frac{V^2}{2 g} \log \left(1+\frac{u^2}{V^2}\right)
1(iii) से \frac{u^2}{V^2}=\tan ^2\left(\frac{g}{V}\right) T रखने पर:
H=\frac{V^2}{2 g} \log \left(1+\tan^2 \left(\frac{g}{V}\right) T \right) \\ H=\frac{V^2}{2 g} \log \sec \left(\frac{g}{V} T\right)
उपर्युक्त प्रश्नों के उत्तर द्वारा गुरुत्वाकर्षण के अधीन उर्ध्वाधर गति (Vertical Motion Under Gravity),वेग के वर्ग-समानुपाती प्रतिरोध के अधीन एक कण की उर्ध्वाधर गति (Vertical Motion of a Particle Under Resistance Varies as Square of Velocity) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Vertical Motion Under Gravity
गुरुत्वाकर्षण के अधीन उर्ध्वाधर गति
(Vertical Motion Under Gravity)
Vertical Motion Under Gravity
गुरुत्वाकर्षण के अधीन उर्ध्वाधर गति (Vertical Motion Under Gravity) कर रहे कण पर
आधारित सवालों को हल करके गुरुत्वाकर्षण के अधीन कण एक ऐसे माध्यम में होकर गिरता है
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.