Maths Beautiful Monsters
गणित के सुंदर राक्षस:कैसे एक विनाशकारी विचार ने आधुनिक गणित का मार्ग प्रशस्त किया का परिचय (Introdiction to Maths Beautiful Monsters:How a destructive idea paved the way for modern math):
- गणित के सुंदर राक्षस:कैसे एक विनाशकारी विचार ने आधुनिक गणित का मार्ग प्रशस्त किया (Maths Beautiful Monsters:How a destructive idea paved the way for modern math)।कई बार हमारी छुपी हुई प्रतिभा को प्रकट होने में कोई विशेष घटना माध्यम होती हैऐसा कई गणितज्ञों और वैज्ञानिकों के उदाहरण मिल जाएंगे जो प्रारम्भ में कोई विशिष्ट अथवा प्रतिभाशाली नहीं थे परन्तु बाद में महान् गणितज्ञ औरतों वैज्ञानिक हुए हैं।इस आर्टिकल इसी प्रकार की घटना का वर्णन किया गया है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:You were not bad at maths
1.गणित के सुंदर राक्षस:कैसे एक विनाशकारी विचार ने आधुनिक गणित का मार्ग प्रशस्त किया (Maths Beautiful Monsters:How a destructive idea paved the way for modern math):
- इसके निर्माता, कार्ल वेइरस्ट्रास के राक्षस की तरह कहीं और से आया था। विश्वविद्यालय में चार साल तक पीने और बाड़ लगाने के बाद वेइरास्ट्रैस खाली हाथ चले गए थे। उन्होंने अंततः एक शिक्षण पाठ्यक्रम लिया और 1850 के दशक में ब्रून्सबर्ग में एक स्कूली शिक्षक के रूप में बिताया। वह छोटे प्रशियाई शहर में जीवन से नफरत करता था, यह एक अकेला अस्तित्व था। उनकी एकमात्र सांसें गणितीय समस्याएं थीं जो उन्होंने कक्षाओं के बीच काम की थीं। लेकिन उनके पास गणित के बारे में बात करने के लिए कोई नहीं था, और न ही अध्ययन करने के लिए कोई तकनीकी पुस्तकालय। यहां तक कि उनके परिणाम भी ब्रंसबर्ग की सीमाओं से बचने में विफल रहे। एक विश्वविद्यालय के शोधकर्ता के रूप में अकादमिक पत्रिकाओं में उन्हें प्रकाशित करने के बजाय, वीरस्ट्रैस ने उन्हें स्कूल प्रॉस्पेक्टस के लेखों में जोड़ा, जो संभावित छात्रों को आर्कन समीकरणों के साथ चकित करते हैं।
- आखिरकार वेइरस्ट्रैस ने अपने एक पत्र को सम्मानित Crelle’s जर्नल को प्रस्तुत किया। जबकि उनके पिछले लेखों ने मुश्किल से एक लहर बना दिया था, इसने रुचि की बाढ़ पैदा की। एबेरियन कार्यों के रूप में जाना जाने वाले समीकरणों के एक उग्र वर्ग से निपटने के लिए वीयरस्टैस ने एक नया तरीका ढूंढ लिया था। कागज में केवल उनके तरीकों की रूपरेखा थी, लेकिन यह गणितज्ञों को समझाने के लिए पर्याप्त था कि वे एक अद्वितीय प्रतिभा के साथ काम कर रहे थे। एक वर्ष के भीतर, कोनिग्सबर्ग विश्वविद्यालय ने वीयरस्टैस को एक डॉक्टरेट की मानद उपाधि दी थी, और इसके तुरंत बाद बर्लिन विश्वविद्यालय ने उन्हें एक प्रोफेसर की पेशकश की। रग्स टू रिच स्टोरी के बौद्धिक समकक्ष होने के बावजूद, उनकी कई पुरानी आदतें बनी रहीं। वह छात्रों के बीच अपने काम को साझा करने के बजाय, शायद ही कभी पेपर प्रकाशित करेंगे। यह केवल प्रकाशन प्रक्रिया नहीं थी जिसके लिए उनके पास बहुत कम संबंध थे: वह गणित की पवित्र गायों को लक्षित करने से भी डरते नहीं थे।
- वेइरास्ट्रैस ने जल्द ही सदी के सबसे प्रख्यात गणितज्ञ ऑगस्टिन-लुई कॉची के शोध का लक्ष्य रखा। कैलूची के अधिकांश कार्य कैलकुलस और परिवर्तन की दरों (या “डेरिवेटिव”) पर केंद्रित हैं। उन्होंने विषय की सबसे महत्वपूर्ण अवधारणाओं को निर्दिष्ट करते हुए एक कैलकुलस शब्दकोश में जो बनाया था, उसे बनाया था। लेकिन जब वेइरास्ट्रैस ने इसकी परिभाषाएँ पढ़ीं, तो उन्होंने पाया कि वे कृमि और अस्पष्ट हैं। बहुत अधिक हाथ लहराते थे, और पर्याप्त विस्तार नहीं था।
- यदि न्यूटन को इस तरह के कार्यों के बारे में पता होता, तो वह कभी भी कलन नहीं बनाता।
उन्होंने गद्य को तार्किक स्थितियों से बदलकर कॉची के शब्दकोश को संशोधित करने का निर्णय लिया। इस प्रारंभिक कार्य के बीच मुख्य एक व्युत्पन्न का पुन: निर्धारण था। एक निश्चित बिंदु पर एक वक्र की ढाल की गणना करने के लिए – और इसलिए इसके परिवर्तन की दर – आइजैक न्यूटन ने मूल रूप से एक पंक्ति पर विचार किया था जो ब्याज के बिंदु और वक्र पर पास के बिंदु से गुजरती थी। उन्होंने उस पास के बिंदु को करीब और करीब ले जाया, जब तक कि रेखा का ढलान वक्र के ढाल के बराबर नहीं था। लेकिन अवधारणा को गणितीय रूप से परिभाषित करना कठिन था। क्या तय किया गया कि क्या दो बिंदु एक-दूसरे के “करीब” थे? - कॉची की क्रिया परिभाषा में, ढाल “निश्चित रूप से एक निश्चित मूल्य के लिए अनिश्चित रूप से दृष्टिकोण करेगी, ताकि एक इच्छा के अनुसार इसे अलग-अलग करके समाप्त हो सके।” वीयरस्ट्रैस ने नहीं सोचा था कि यह पर्याप्त स्पष्ट था। वह अधिक व्यावहारिक परिभाषा चाहता था, इसलिए अवधारणा को एक सूत्र में बदलने का फैसला किया। अमूर्त विचारों में हेरफेर करने के बजाय, गणितज्ञ इसके बजाय समीकरणों को पुनर्व्यवस्थित करने में सक्षम होंगे। ऐसा करते हुए, वह अपने राक्षस के लिए नींव रख रहा था।
- उस समय, गणितज्ञों ने प्रकृति से उनकी बहुत प्रेरणा ली। जब न्यूटन ने पहली बार पथरी का विकास किया, तो वह भौतिक दुनिया से प्रेरित था: एक ग्रह का प्रक्षेपवक्र, एक पेंडुलम का झूलना, गिरने वाले फल की गति। इस सोच के कारण गणितीय संरचनाओं के बारे में ज्यामितीय अंतर्ज्ञान हुआ। उन्हें उसी तरह से समझाना चाहिए जैसे कि एक भौतिक वस्तु होगी। नतीजतन, कई गणितज्ञ “निरंतर” कार्यों पर ध्यान केंद्रित करते हैं। वैचारिक रूप से, ये ऐसे कार्य हैं जिन्हें कागज से कलम उठाए बिना खींचा जा सकता है। समय के साथ गिरने वाले सेब की गति को प्लॉट करें और यह एक ठोस रेखा होगी; कोई अंतराल या अचानक कूद नहीं होगा। एक सतत कार्य था, यह सोचा गया था, एक प्राकृतिक।
Also Read This Article:Interest enhancing approaches to mathematics curriculum design
2.परम्परागत ज्ञान (Conventional wisdom):
- परम्परागत ज्ञान का मानना था कि किसी भी निरंतर वक्र के लिए, सभी बिंदुओं की एक निश्चित संख्या के आधार पर ढाल को खोजना संभव था। यह अंतर्ज्ञान से मेल खाता प्रतीत होता है: एक पंक्ति में कुछ दांतेदार बिट्स हो सकते हैं, लेकिन हमेशा कुछ खंड होंगे जो “सुचारू” थे। फ्रांसीसी भौतिक विज्ञानी और गणितज्ञ आंद्रे-मैरी एम्पीयर ने इस दावे का एक प्रमाण भी प्रकाशित किया था। उनका तर्क “सहज रूप से स्पष्ट” तथ्य पर बनाया गया था कि एक निरंतर वक्र में वृद्धि, कमी या सपाट रहने वाले खंड होने चाहिए। जिसका अर्थ था कि इन क्षेत्रों में ढाल की गणना करना संभव है। Ampère ने यह नहीं सोचा कि तब क्या हुआ जब अनुभाग असीम रूप से छोटे हो गए, लेकिन उन्होंने दावा किया कि उन्हें इसकी आवश्यकता नहीं थी। उनका दृष्टिकोण सामान्य था कि वे उन बातों पर विचार करने से बचें, जो ” इनफिनिटी पेटिट्स ” थीं, अधिकांश गणितज्ञ उसके तर्क से खुश थे: 19 वीं शताब्दी के मध्य तक, लगभग हर कैलकुलस टेक्स्टबुक में एम्पीयर के प्रमाण को उद्धृत किया गया था।
लेकिन 1860 के दशक के दौरान, एक अजीब प्राणी के बारे में अफवाहें फैलने लगीं, एक गणितीय समारोह जिसने एम्पीयर के प्रमेय का खंडन किया। जर्मनी में, महान बर्नहार्ड रीमैन ने अपने छात्रों से कहा कि उन्हें एक ऐसे निरंतर कार्य के बारे में पता है जिसमें कोई सुचारू खंड नहीं है, और जिसके लिए किसी भी बिंदु पर फ़ंक्शन के व्युत्पन्न की गणना करना असंभव था। रीमैन ने एक प्रमाण प्रकाशित नहीं किया, और न ही जिनेवा विश्वविद्यालय में चार्ल्स सेलरियर, जिन्होंने लिखा – यह लिखने के बावजूद कि उन्होंने कुछ “बहुत महत्वपूर्ण और मुझे लगता है कि नया खोजा” – एक फ़ोल्डर में काम को भर दिया जो केवल उसके बाद सार्वजनिक हो जाएगा दशकों बाद मृत्यु। फिर भी अगर दावों पर विश्वास किया जाए, तो इसका मतलब है कि पथरी की बहुत नींव पड़ी है। इस जीव ने गणितीय सिद्धांत और उस भौतिक अवलोकन के बीच खुशहाल रिश्ते को तोड़ने की धमकी दी थी जिस पर यह आधारित था। कैलकुलस हमेशा से ही ग्रहों और तारों की भाषा रहा था, लेकिन अगर कोई गणितीय कार्य हो जो विषय के केंद्रीय विचारों का खंडन करता हो तो प्रकृति एक विश्वसनीय प्रेरणा कैसे हो सकती है? - दैत्य आखिरकार 1872 में पैदा हुआ, जब कार्ल वेइरस्ट्रास ने घोषणा की कि उसने एक ऐसा कार्य पाया है जो निरंतर था और फिर भी किसी भी बिंदु पर सहज नहीं था। उन्होंने इसे ब्रह्मांड के कार्यों के असीम रूप से लंबे अनुक्रम के साथ जोड़कर बनाया था:
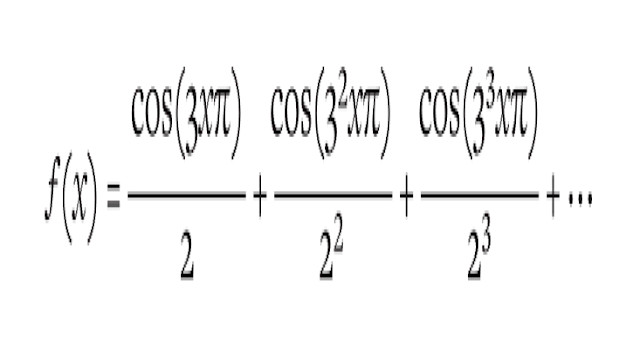
Maths Beautiful Monsters[/capion]
- एक समारोह के रूप में,यह बदसूरत और अजीब था। यह भी स्पष्ट नहीं था कि एक ग्राफ पर प्लॉट किए जाने पर यह कैसा दिखेगा। लेकिन वेयोरस्टैस के लिए यह कोई मायने नहीं रखता था। उनके प्रमाण में आकृतियों के बजाय समीकरण शामिल थे और यही उनकी घोषणा को इतना शक्तिशाली बनाता था। न केवल उसने एक राक्षस बनाया था, उसने इसे ठोस तर्क से बनाया था। उन्होंने एक व्युत्पन्न की अपनी नई, कठोर परिभाषा ली थी और दिखाया कि इस नए कार्य के लिए किसी एक की गणना करना असंभव था।
- परिणाम ने गणित समुदाय को सदमे की स्थिति में फेंक दिया। फ्रांसीसी गणितज्ञ ilemile Picard ने बताया कि यदि न्यूटन को इस तरह के कार्यों के बारे में पता होता, तो वह कभी भी पथरी नहीं बनाता। प्रकृति की भौतिकी के बारे में विचारों का दोहन करने के बजाय, वह कठोर गणितीय बाधाओं पर चढ़ने की कोशिश कर रहा होगा। राक्षस भी पिछले शोध पर रौंदने लगा। परिणाम जो “सिद्ध” हो गए थे, बकसुआ करने लगे। Ampère ने अपनी चिकनाई प्रमेय को साबित करने के लिए कॉची द्वारा इष्ट अस्पष्ट परिभाषाओं का उपयोग किया था। अब, उसके तर्क ध्वस्त होने लगे। अतीत की अस्पष्ट धारणा राक्षस के खिलाफ निराशाजनक थी। इससे भी बदतर, यह स्पष्ट नहीं था कि गणितीय प्रमाण क्या है। पिछली दो शताब्दियों की सहज, ज्यामिति-आधारित दलीलें कम उपयोग की लगती थीं। अगर गणित ने राक्षस को दूर भगाने की कोशिश की, तो वह दृढ़ हो जाएगा। एक विचित्र समीकरण के साथ, वीयरस्ट्रैस ने प्रदर्शित किया था कि भौतिक अंतर्ज्ञान एक विश्वसनीय आधार नहीं था जिस पर गणितीय सिद्धांतों का निर्माण किया जा सके।
- स्थापित गणितज्ञों ने परिणाम को अलग करने की कोशिश की, यह तर्क देते हुए कि यह अजीब और अनावश्यक था। उन्हें डर था कि पेडेंट और संकटमोचक अपने प्रिय विषय को छिपा रहे थे। सोरबोन में, चार्ल्स हरमाइट ने लिखा, “मैं बिना किसी व्युत्पत्ति के कार्यों के इस विलापणीय संकट से आतंक और आतंक के साथ मुड़ता हूं।” हेनरी पोनकारे – जो इस तरह के कार्यों को राक्षस कहने वाले पहले व्यक्ति थे – वेइरास्ट्रैस के इस कार्य को “सामान्य ज्ञान के खिलाफ एक आक्रोश” कहा। “उन्होंने दावा किया कि कार्य एक अभिमानी व्याकुलता थी, और विषय के लिए बहुत कम उपयोग। उन्होंने कहा, “हमारे पूर्वजों के तर्क को गलत दिखाने के उद्देश्य से उनका आविष्कार किया गया है,” उन्होंने कहा, “और हमें उनमें से कुछ भी कभी नहीं मिलेगा।”
कई पुराने रक्षक गणित के जंगल में वीयरस्टैस के राक्षस को छोड़ना चाहते थे। यह मदद नहीं करता था कि कोई भी उस जानवर के आकार की कल्पना नहीं कर सकता है जिसके साथ वे व्यवहार कर रहे थे – केवल कंप्यूटर के आगमन के साथ ही इसे साजिश करना संभव हो गया था। इसके छिपे हुए रूप ने गणित समुदाय के लिए यह समझ पाना मुश्किल कर दिया कि इस तरह के समारोह का अस्तित्व कैसे हो सकता है। वेइरास्ट्रास की शैली का प्रमाण भी कई गणितज्ञों के लिए अपरिचित था। उनके तर्क में दर्जनों तार्किक कदम शामिल थे, और कई पृष्ठों तक चले गए। विचारों के निशान सूक्ष्म और तकनीकी रूप से मांग कर रहे थे, जिस तरह से मार्गदर्शन करने के लिए कोई वास्तविक जीवन एनालॉग नहीं था। वृत्ति इससे बचने की थी।
- लेकिन राक्षसों को ठंड से अपना रास्ता खोजने की आदत है। वास्तव में कई अवधारणाएँ जो अब स्पष्ट प्रतीत होती हैं, यहां तक कि आवश्यक हैं, एक बार राक्षस थे। सदियों से गणितज्ञों द्वारा नकारात्मक संख्याओं को दूर किया गया था। प्राचीन यूनानी, जो मुख्य रूप से ज्यामिति से निपटते थे, ने उनकी कोई आवश्यकता नहीं देखी। न ही मध्यकालीन शिक्षाविदों ने ग्रीक विचारों को अपनाया। इस राक्षस की छाया कभी-कभार आज भी दिखाई देती है, जैसे कि जब कोई बच्चा पूछता है कि दो नकारात्मक संख्याओं को एक साथ गुणा करना एक सकारात्मक क्यों पैदा करता है। लेकिन कुल मिलाकर जानवर को बांध दिया गया है; कोई भी इसे फिर से निर्वासित करने का सपना नहीं देखेगा।
- इसी तरह से, वीयरस्ट्रास के राक्षस को स्वीकृति मिलनी शुरू हुई। 1904 में, अल्बर्ट आइंस्टीन ने भौतिकविदों को “ब्राउनियन मोशन” के विचार से परिचित कराया: एक तरल पदार्थ में कण, उन्होंने कहा, एक यादृच्छिक पथ का पालन करें क्योंकि द्रव अणु लगातार उन्हें चारों ओर दस्तक दे रहे हैं। टक्कर इतनी लगातार (10²¹ प्रति सेकंड से अधिक) होती है कि माइक्रोस्कोप कितना भी अच्छा हो, या अवलोकन कितना ही विस्तृत क्यों न हो, प्रक्षेपवक्र कभी भी सुचारू नहीं होते हैं। व्यावहारिक स्तर पर, एक व्युत्पन्न खोजना संभव नहीं है। यदि शोधकर्ता ऐसी समस्याओं के साथ काम करना चाहते हैं, तो उन्हें वेइरास्ट्रैस के राक्षस का सामना करने की आवश्यकता होगी – और ठीक यही आइंस्टीन ने किया। ब्राउनियन गति के लिए उनके सिद्धांत ने उन कार्यों का उपयोग किया जो कि असीम रूप से दांतेदार थे। इसने एक पुरानी मिसाल कायम की: भौतिकविदों ने ब्राउनियन गति के लिए प्रॉक्सी के रूप में गैर-चिकनी कार्यों का उपयोग किया है।
- एक बार जब यह स्पष्ट हो गया कि तथाकथित “वीयरस्ट्रैस फंक्शन” वास्तव में काफी उपयोगी था, शोधकर्ताओं ने गैर-चिकनी कार्यों को इनायत से संभालने के तरीके विकसित करना शुरू कर दिया। एक तरल में एक कण के पथ का विश्लेषण करने की कोशिश करने के बजाय, वे कई कणों के औसत व्यवहार को देखेंगे। कितनी दूर वे यात्रा की संभावना थी? वे किसी दिए गए बिंदु पर कब पहुँच सकते हैं? ब्राउनियन गति के बाहर, गणितज्ञों ने भी पथरी के बुनियादी साधनों पर पुनर्विचार करना शुरू कर दिया। परिवर्तन की दरों को हमेशा ज्यामितीय रूप से मापा जाने वाले वक्र के तहत दूरी और क्षेत्रों के संदर्भ में परिभाषित किया गया था। लेकिन जब कार्य सुचारू नहीं थे, तो इन विचारों का कोई मतलब नहीं था।
- टोक्यो विश्वविद्यालय में, Kiyoshi Itō ने संभावनाओं के संदर्भ में सोचकर समस्या का एक रास्ता खोज लिया। यह एक अपरंपरागत था, जोखिम भरा, रणनीति का उल्लेख नहीं करने के लिए: 1940 के दशक के दौरान, शायद ही किसी ने संभावना सिद्धांत को एक कठोर विषय के रूप में देखा। फिर भी It Yet कायम रहा। उन्होंने यादृच्छिक प्रक्रियाओं जैसे कार्यों का व्यवहार किया, और वेइरास्ट्रैस की परिभाषाओं का एक नई, संभाव्यता-आधारित भाषा में अनुवाद किया। दो यादृच्छिक प्रक्रियाएं एक साथ “करीब” थीं, उन्होंने कहा, यदि अपेक्षित परिणाम समान थे। उन्होंने एक गणितीय फ़ंक्शन को संभालने के लिए एक विधि पेश की जो एक गैर-चिकनी मात्रा पर निर्भर करती है – जैसे ब्राउनियन गति – दूरी की तरह अधिक पारंपरिक चर के बजाय। अपने नए तरीकों का उपयोग करते हुए, उन्होंने यह निर्धारित करने के लिए “इट्स लेम्मा” प्राप्त किया कि इस तरह के फ़ंक्शन समय के साथ कैसे बदलते हैं।
- 1970 के दशक तक, इटो का काम गणित के एक पूरे नए क्षेत्र में विकसित हो गया था, जिसे स्टॉचस्टिक कैलकुलस (गणितज्ञ ऐसी चीजें कहते हैं जो यादृच्छिक “स्टोचस्टिक” हैं)। यह उपकरण और प्रमेयों के एक पूरे नए सेट के साथ आया था, जैसे कि कैलकुलस के पास था। आज, स्टोकेस्टिक पथरी का उपयोग सभी प्रकार की घटनाओं का अध्ययन करने के लिए किया जाता है, एक मस्तिष्क में न्यूरॉन्स की गोलीबारी से लेकर आबादी तक फैलने वाली बीमारियों तक। यह वित्तीय गणित के केंद्र में भी है, जहां यह बैंकों को विकल्प कीमतों का अनुमान लगाने में मदद करता है। यह स्टॉक मूल्य के ऊबड़ व्यवहार के लिए जिम्मेदार हो सकता है, और इसलिए यह बताता है कि समय के साथ एक विकल्प का मूल्य कैसे बदलता है। परिणामी समीकरण, जिसे ब्लैक-स्कोल्स फॉर्मूला के रूप में जाना जाता है, अब दुनिया भर में ट्रेडिंग फ्लोर पर उपयोग किया जाता है। फिर भी It Yet हमेशा हैरान था जब उसने बैंकरों से प्लेडिट जीते। एक शुद्ध गणितज्ञ के रूप में, उन्होंने अपने काम के अपने अनुप्रयोगों के लिए प्रसिद्ध होने की उम्मीद नहीं की थी।
- $ 1 मिलियन का पुरस्कार लावारिस बना हुआ है। कई मायनों में, यह एक फिरौती है।
वेइरस्ट्रास के राक्षस ने ज्यामिति में भी चीजों को हिला दिया। 19 वीं शताब्दी के अंत में, स्वीडिश गणितज्ञ हेल्गे वॉन कोच गैर-चिकने कार्यों के विचार में रुचि रखते थे, लेकिन वह उनके आकार को देखना चाहते थे। वह एक आकृति बनाने के लिए निकल गया (एक फ़ंक्शन के बजाय) जो कहीं भी चिकना नहीं था, और इसलिए यह दर्शाता है कि एक ही राक्षस बीजगणित और ज्यामिति दोनों में दुबके हुए थे। वह वीयरस्टैस फ़ंक्शन को आकर्षित करने में सक्षम नहीं हो सकता है, लेकिन वह अपने चचेरे भाई की तस्वीर लेने में सक्षम होगा। एक जूनियर प्रोफेसर के रूप में एक अस्थायी नौकरी से दूसरे में नौकरी करते हुए समस्या पर काम करते हुए, वॉन कोच ने 1904 में अपने प्राणी को पाया। एक समभुज त्रिभुज लेकर निर्माण किया, फिर प्रत्येक पक्ष में तीन छोटे त्रिकोणों को जोड़ा, और अनिश्चित काल तक ऐसा करना जारी रखा। एक ज्यामितीय आकार जो निरंतर था लेकिन कोई व्युत्पन्न नहीं था। आकार की विशिष्ट उपस्थिति का मतलब है कि यह जल्द ही “कोच हिमपात का एक खंड” के रूप में जाना जाने लगा। - कोच समीकरणों और कार्यों की दुनिया से परे वीयरस्ट्रास के राक्षस का विस्तार करने में सफल रहे। लेकिन उसके परिणाम के बारे में कुछ और उल्लेखनीय था। करीब से निरीक्षण करने पर, यह पता चला कि उनकी बर्फ के टुकड़े में एक बड़ी आत्म-समानता थी: बर्फ के टुकड़े के एक विशेष खंड को आवर्धित करें और यह ज़ूम-आउट आकार के समान दिखाई देगा। कई वर्षों बाद, यह स्पष्ट हो जाएगा कि वीयरस्ट्रैस फ़ंक्शन के पास समान संपत्ति थी।
- जैसे-जैसे समय बीतता गया, यह आत्म-समानता सभी प्रकार के स्थानों में पकने लगी। 1980 के दशक के दौरान “फ्रैक्टल” वस्तुओं के विचार को लोकप्रिय बनाने के लिए बेनोइट मैंडलब्रॉट के सेमिनल का काम होगा, जिसमें ऐसी आकृतियाँ थीं, जिन्हें छोटे और छोटे लंबाई के पैमाने पर दोहराया गया था। तटरेखा और बादलों से लेकर पौधे और रक्त वाहिकाओं तक, गणितज्ञों ने पाया कि भग्न प्रकृति में सर्वव्यापी थे। कोच के बर्फ के टुकड़े की तरह, कोई भी चिकना नहीं था। वे कैसे हो सकते हैं? यदि आकार में चिकनी अनुभाग होते हैं, तो पैटर्न पर्याप्त रूप से बढ़ जाने पर गायब हो जाएगा। जैसा कि कोच ने पाया था, एक गैर-चिकनी आकार प्राप्त करने का सबसे सरल तरीका एक भग्न वस्तु का निर्माण करना था। शायद यह अपरिहार्य था कि वीयरस्ट्रैस का काम गणितज्ञों को आत्म-समान प्रतिमानों के लिए मार्गदर्शन करेगा, शोधकर्ताओं को जटिल, सुंदर संरचनाओं की दुनिया में पेश करेगा।
- वीयरस्ट्रास का राक्षस वर्तमान समय में भी अपना काम जारी रखे हुए है। नवियर-स्टोक्स समीकरण एक तरल पदार्थ की गति का वर्णन करते हैं और आधुनिक द्रव की गतिशीलता और वायुगतिकी को रेखांकित करते हैं, जो विमान के डिजाइन से लेकर मौसम की भविष्यवाणी तक सब कुछ चलाते हैं। हालांकि, हालांकि वे पहली बार 1840 के दशक में विकसित हुए थे, गणितज्ञ अभी भी नहीं जानते हैं कि क्या वे हमेशा हल हो सकते हैं। 2000 में, क्ले मैथमेटिक्स इंस्टीट्यूट ने किसी को भी $ 1 मिलियन का पुरस्कार देने की पेशकश की, जो यह दिखा सके कि समीकरणों के हमेशा सरल समाधान होते हैं – या इसके विपरीत एक उदाहरण खोजें। इस समस्या को गणित की छह सबसे महत्वपूर्ण समस्याओं में से एक माना जाता है क्योंकि नवियर-स्टोक्स समीकरणों के व्यापक उपयोग के बावजूद, गणितज्ञों को यह नहीं पता है कि समीकरण हमेशा शारीरिक रूप से प्रशंसनीय परिणाम देते हैं या नहीं। $ 1 मिलियन का पुरस्कार लावारिस बना हुआ है। कई मायनों में यह एक फिरौती है, जो गणितज्ञों को परेशान करने वाले राक्षसों का शिकार करने के लिए प्रोत्साहित करता है।
- तरल गतिकी से लेकर वित्त तक, वेइरास्ट्रैस फ़ंक्शन जैसे जीवों ने गणित और प्राकृतिक दुनिया के बीच संबंधों के बारे में हमारे विचारों को चुनौती दी है। वेइरास्ट्रैस के समय के आसपास के गणितज्ञ मानते थे कि सबसे उपयोगी गणित प्रकृति से प्रेरित था, और वेइरास्ट्रास का काम उस परिभाषा में फिट नहीं था। लेकिन स्टोकेस्टिक पथरी और मैंडेलब्रोट के भग्न ने उन्हें गलत साबित कर दिया है। यह पता चला है कि वास्तविक दुनिया में – गन्दा, जटिल वास्तविक दुनिया – राक्षस हर जगह हैं। “प्रकृति ने गणितज्ञों पर एक मजाक खेला है,” जैसा कि मैंडेलब्रोट ने कहा था। यहां तक कि वेइरास्ट्रैस खुद भी छल का शिकार हुए। उन्होंने तर्क दिया कि गणित केवल भौतिक टिप्पणियों पर आधारित नहीं होना चाहिए। उनके अनुयायियों का मानना था कि न्यूटन वास्तविक जीवन के अंतर्ज्ञान से विवश थे और एक बार, इन सीमाओं से मुक्त होने पर, खोजे जाने वाले विशाल, सुरुचिपूर्ण नए सिद्धांत थे। उन्होंने सोचा कि गणित को अब प्रकृति की आवश्यकता नहीं होगी। फिर भी वीयरस्ट्रास के राक्षस ने इसके विपरीत होने का खुलासा किया है। प्रकृति और गणित के बीच का संबंध किसी की भी कल्पना से कहीं अधिक गहरा है।
- एडम कुचारस्की लंदन स्कूल ऑफ हाइजीन एंड ट्रॉपिकल मेडिसिन में गणितीय महामारी विज्ञान में एक शोध साथी हैं।
Also Read This Article:Beautiful Monster
- इस आर्टिकल में गणित के सुंदर राक्षस:कैसे एक विनाशकारी विचार ने आधुनिक गणित का मार्ग प्रशस्त किया (Maths Beautiful Monsters:How a destructive idea paved the way for modern math) के बारे में बताया गया है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
