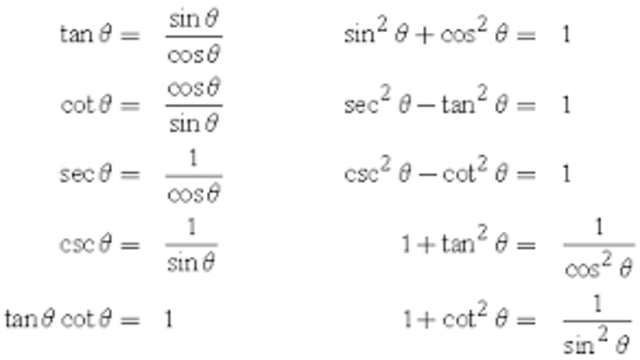1.त्रिकोणमितीय अनुपातों में परस्पर सम्बन्ध (Relation Between Trigonometric Ratios)-

• त्रिकोणमितीय अनुपातों में परस्पर सम्बन्ध (Relation Between Trigonometric Ratios) के द्वारा त्रिकोणमितीय अनुपातों के मान ज्ञात करेंगे।
• (a.)त्रिकोणमितीय अनुपातों में परस्पर सम्बन्ध कक्षा 10 (Relation between trigonometric ratios class 10), त्रिकोणमिति फार्मूला (Trigonometry formula)-
  किसी समकोण त्रिभुज OMP में कोण के लिए भुजा PM लम्ब,भुजा OM आधार तथा भुजा OP कर्ण है।
  

  Relation Between Trigonometric Ratios

• (1.) $\sin { \theta } cosec\theta =1\\ \sin { \theta } =\frac { PM }{ OP } ............(1)$
• तथा $cosec\theta =\frac { OP }{ PM } ........(2)$
  (1) व (2) से गुणा करने पर-

$\sin { \theta } cosec\theta =\frac { PM }{ OP } \times \frac { OP }{ PM } =1$
अर्थात् $\sin { \theta } cosec\theta =1\\ \Rightarrow \sin { \theta } =\frac { 1 }{ cosec\theta } \\ \Rightarrow cosec\theta =\frac { 1 }{ \sin { \theta } }$
अतः $\sin { \theta } तथा  cosec\theta$ परस्पर व्युत्क्रम है।

• (2.) $\cos { \theta } \sec { \theta } =1\\ \cos { \theta } =\frac { आधार }{ कर्ण } =\frac { OM }{ OP } ......(3)$
  और $\sec { \theta } =\frac { कर्ण }{ आधार } =\frac { OP }{ OM } .....(4)$
  समीकरण (3) व (4) को परस्पर गुणा करने पर-

$\cos { \theta } \sec { \theta } =\frac { OM }{ OP } \times \frac { OP }{ OM } =1$
अर्थात् $\cos { \theta } \sec { \theta } =1\\ \Rightarrow \cos { \theta } =\frac { 1 }{ \sec { \theta } } \\ \Rightarrow \sec { \theta } =\frac { 1 }{ \cos { \theta } }$
अतः $\cos { \theta }  तथा \sec { \theta }$  परस्पर व्युत्क्रम है।

• (3.)$\tan { \theta } \cot { \theta } =1\\ \tan { \theta } =\frac {लम्ब }{आधार } =\frac { PM }{ OM } .....(5)$
  और $\cot { \theta } =\frac {आधार }{लम्ब }=\frac { OM }{ PM } .........(6)$
  समीकरण (5) व (6) को परस्पर गुणा करने पर-

$\tan { \theta } \cot { \theta } =\frac { PM }{ OM } .\frac { OM }{ PM } =1$
अर्थात्  $\tan { \theta } \cot { \theta } =1\\ \Rightarrow \tan { \theta } =\frac { 1 }{ \cot { \theta } } \\ \Rightarrow \cot { \theta } =\frac { 1 }{ \tan { \theta } }$
अतः $\tan { \theta }  तथा \cot { \theta }$  परस्पर व्युत्क्रम है।

• (4.)$\tan { \theta } =\frac { \sin { \theta } }{ \cos { \theta } }$
  समीकरण (1) व (3) से-

$\frac { \sin { \theta } }{ \cos { \theta } } =\frac { \frac { PM }{ OP } }{ \frac { OM }{ OP } } \\ =\frac { PM }{ OP } .\frac { OP }{ OM } \\ =\frac { PM }{ OM } \\ =\frac {लम्ब }{आधार } \\ \frac { \sin { \theta } }{ \cos { \theta } } =\tan { \theta }$
अर्थात् $\tan { \theta } =\frac { \sin { \theta } }{ \cos { \theta } }$

• (5.) $\cot { \theta } =\frac { \cos { \theta } }{ \sin { \theta } }$
  समीकरण (1) व (3) से-

$\frac { \cos { \theta } }{ \sin { \theta } } =\frac { \frac { OM }{ OP } }{ \frac { PM }{ OP } } \\ \frac { \cos { \theta } }{ \sin { \theta } } =\frac { OM }{ OP } .\frac { OP }{ PM } \\ \Rightarrow \frac { \cos { \theta } }{ \sin { \theta } } =\frac { OM }{ PM } \\ =\frac {आधार }{लम्ब } \\ =\cot { \theta }$
अर्थात् $\cot { \theta } =\frac { \cos { \theta } }{ \sin { \theta } }$
(b)त्रिकोणमितीय सर्वसमिकाएं कक्षा 10 (Trigonometric identities class 10)-

• (6.)$\sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } =1$

समीकरण (1) व (3) से-
$\sin { \theta } =\frac { PM }{ OP }  एवं \cos { \theta } =\frac { OM }{ OP }$
वर्ग करके जोड़ने पर-

$\sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } ={ \left( \frac { PM }{ OP } \right) }^{ 2 }+{ \left( \frac { OM }{ OP } \right) }^{ 2 }\\ \quad  =\frac { { PM }^{ 2 }+{ OM }^{ 2 } }{ { OP }^{ 2 } } =\frac { { OP }^{ 2 } }{ { OP }^{ 2 } }$[बौधायन सूत्र से ${ OP }^{ 2 }={ PM }^{ 2 }+{ OM }^{ 2 }$]

$\Rightarrow \sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } =1$

• (7.) $1+\tan ^{ 2 }{ \theta } =\sec ^{ 2 }{ \theta } \\ \tan { \theta } =\frac { PM }{ OM } \\ 1+\tan ^{ 2 }{ \theta } =1+\frac { { PM }^{ 2 } }{ { OM }^{ 2 } } \\  \quad =\frac { { PM }^{ 2 }+{ OM }^{ 2 } }{ { OP }^{ 2 } } \\ \quad =\frac { { OP }^{ 2 } }{ { OM }^{ 2 } }$[बौधायन सूत्र से ${ OP }^{ 2 }={ PM }^{ 2 }+{ OM }^{ 2 }$]

$\quad =\sec ^{ 2 }{ \theta }[\sec { \theta }=\frac { OP }{ OM }] \\ \Rightarrow 1+\tan ^{ 2 }{ \theta } =\sec ^{ 2 }{ \theta }$
वैकल्पिक विधि-

$\sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } =1$
दोनों पक्षों में $\cos ^{ 2 }{ \theta }$ से भाग देने पर-

$\frac { \sin ^{ 2 }{ \theta } }{ \cos ^{ 2 }{ \theta } } +\frac { \cos ^{ 2 }{ \theta } }{ \cos ^{ 2 }{ \theta } } =\frac { 1 }{ \cos ^{ 2 }{ \theta } } \\ \Rightarrow \tan ^{ 2 }{ \theta } +1=\sec ^{ 2 }{ \theta } [\tan { \theta } =\frac { \sin { \theta } }{ \cos { \theta } } ,\cos { \theta } =\frac { 1 }{ \sec { \theta } } ]$

$\Rightarrow 1+\tan ^{ 2 }{ \theta } =\sec ^{ 2 }{ \theta }$

• (8.)$1+\cot ^{ 2 }{ \theta } ={ cosec }^{ 2 }\theta \\ \cot { \theta } =\frac { OM }{ PM } \\ 1+\cot ^{ 2 }{ \theta } =1+{ \left( \frac { OM }{ OP } \right) }^{ 2 }=1+\frac { { OM }^{ 2 } }{ { OP }^{ 2 } } \\ \quad=\frac { { PM }^{ 2 }+{ OM }^{ 2 } }{ { PM }^{ 2 } } \\ \quad  =\frac { { OP }^{ 2 } }{ { PM }^{ 2 } }$[बौधायन सूत्र से ${ OP }^{ 2 }={ PM }^{ 2 }+{ OM }^{ 2 }]$

=${ cosec }^{ 2 }\theta [\because cosecA=\frac { OP }{ PM } ]$
वैकल्पिक विधि:

$\sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } =1$
दोनों पक्षों में $\sin ^{ 2 }{ \theta }$ से भाग देने पर-

$\frac { \sin ^{ 2 }{ \theta } }{ \sin ^{ 2 }{ \theta } } +\frac { \cos ^{ 2 }{ \theta } }{ \sin ^{ 2 }{ \theta } } =\frac { 1 }{ \sin ^{ 2 }{ \theta } } \\ \Rightarrow 1+\cot ^{ 2 }{ \theta } ={ cosec }^{ 2 }\theta [\cot { \theta } =\frac { \cos { \theta } }{ \sin { \theta } } ,cosec\theta =\frac { 1 }{ \sin { \theta } } ]$

आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Trigonometric Ratios of Acute Angle

2. त्रिकोणमितीय अनुपातों में परस्पर सम्बन्ध के उदाहरण (Relation Between Trigonometric Ratios Examples)-

त्रिकोणमितीय अनुपातों में सम्बन्धों द्वारा हल कीजिए: (Solve by Relation Between Trigonometric Ratios:)
Example-1. यदि $cosecA=\frac { 5 }{ 4 }$  हो तो $\cot { A } ,\sin { A } ,\cos { A }$ का मान ज्ञात कीजिए।

Ans:-$cosecA=\frac { 5 }{ 4 } \qquad \qquad \qquad \\ 1+\cot ^{ 2 }{ A } ={ cosec }^{ 2 }A\\ \Rightarrow 1+\cot ^{ 2 }{ A } ={ \left( \frac { 5 }{ 4 } \right) }^{ 2 }\\ \Rightarrow \cot ^{ 2 }{ A } =\frac { 25 }{ 16 } -1\\ \Rightarrow \cot ^{ 2 }{ A } =\frac { 9 }{ 16 } \\ \Rightarrow \cot { A } =\pm \frac { 3 }{ 4 } \\ \cot { A } =\frac { 3 }{ 4 }$ (क्योंकि A न्यून कोण है)
$\sin { A } =\frac { 1 }{ cosecA } \\ \Rightarrow \sin { A } =\frac { 1 }{ \frac { 5 }{ 4 } } =\frac { 4 }{ 5 } \\ \Rightarrow \sin ^{ 2 }{ A } +\cos ^{ 2 }{ A } =1\\ \Rightarrow { \left( \frac { 4 }{ 5 } \right) }^{ 2 }+\cos ^{ 2 }{ A } =1\\ \Rightarrow \frac { 16 }{ 25 } +\cos ^{ 2 }{ A } =1\\ \Rightarrow \cos ^{ 2 }{ A } =1-\frac { 16 }{ 25 } =\frac { 25-16 }{ 25 } \\ \Rightarrow \cos ^{ 2 }{ A } =\frac { 9 }{ 25 } \\ \Rightarrow \cos { A } =\pm \frac { 3 }{ 5 } \\ \Rightarrow \cos { A } =\frac { 3 }{ 5 }$(क्योंकि न्यून कोण है)
अतः $\cot { A } =\frac { 3 }{ 5 } ,\sin { A } =\frac { 4 }{ 5 } ,\cos { A } =\frac { 3 }{ 5 }$
Example-2. यदि $\tan { A } =\frac { 20 }{ 21 }$ हो तो $\cos { A }$ तथा $\sin { A }$ का मान ज्ञात कीजिए।
Solution-$\tan { A } =\frac { 20 }{ 21 } \\ 1+\tan ^{ 2 }{ A } =\sec ^{ 2 }{ A } \\ \Rightarrow 1+{ \left( \frac { 20 }{ 21 } \right) }^{ 2 }=\sec ^{ 2 }{ A } \\ \Rightarrow \sec ^{ 2 }{ A } =1+\frac { 400 }{ 441 } =\frac { 441+400 }{ 441 } =\frac { 841 }{ 441 } \\ \Rightarrow \sec { A } =\pm \frac { 29 }{ 21 } \\ \Rightarrow \sec { A } =\frac { 29 }{ 21 }$ (क्योंकि A न्यून कोण है)
$\cos { A } =\frac { 1 }{ \sec { A } } \\ \Rightarrow \cos { A } =\frac { 1 }{ \frac { 29 }{ 21 } } \\ \Rightarrow \cos { A } =\frac { 21 }{ 29 } \\ \sin ^{ 2 }{ A } +\cos ^{ 2 }{ A } =1\\ \Rightarrow \sin ^{ 2 }{ A } +{ \left( \frac { 21 }{ 29 } \right) }^{ 2 }=1\\ \Rightarrow \sin ^{ 2 }{ A } +\frac { 441 }{ 841 } =1\\ \Rightarrow \sin ^{ 2 }{ A } =1-\frac { 441 }{ 841 } \\ \Rightarrow \sin ^{ 2 }{ A } =\frac { 841-441 }{ 841 } \\ \Rightarrow \sin ^{ 2 }{ A } =\frac { 400 }{ 841 } \\ \Rightarrow \sin { A } =\pm \frac { 20 }{ 29 } \\ \Rightarrow \sin { A } =\frac { 20 }{ 29 }$ (क्योंकि A न्यून कोण है)

$\cos { A } =\frac { 21 }{ 29 } ,\sin { A } =\frac { 20 }{ 29 }$
Example-3.यदि $\sin { A } =\frac { 3 }{ 5 }$ हो तो $\cos { A }$ और $\tan { A }$ के मान ज्ञात कीजिए।
Solution-$\sin { A } =\frac { 3 }{ 5 } \\ \sin ^{ 2 }{ A } +\cos ^{ 2 }{ A } =1\\ \Rightarrow { \left( \frac { 3 }{ 5 } \right) }^{ 2 }+\cos ^{ 2 }{ A } =1\\ \Rightarrow \frac { 9 }{ 25 } +\cos ^{ 2 }{ A } =1\\ \Rightarrow \cos ^{ 2 }{ A } =1-\frac { 9 }{ 25 } =\frac { 25-9 }{ 25 } \\ \Rightarrow \cos ^{ 2 }{ A } =\frac { 16 }{ 25 } \\ \Rightarrow \cos { A } =\pm \frac { 4 }{ 5 } \\ \Rightarrow \cos { A } =\frac { 4 }{ 5 }$ (क्योंकि A न्यून कोण है)

$\tan { A } =\frac { \sin { A } }{ \cos { A } } =\frac { \frac { 3 }{ 5 } }{ \frac { 4 }{ 5 } } \\ \Rightarrow \tan { A } =\frac { 3 }{ 4 } \\ \cos { A } =\frac { 4 }{ 5 } ,\tan { A } =\frac { 3 }{ 4 }$
Example-4. यदि $\cos { B } =\frac { 1 }{ 3 }$  हो तो शेष त्रिकोणमितीय अनुपात ज्ञात कीजिए।
Solution-$\cos { B } =\frac { 1 }{ 3 } \\ \sin ^{ 2 }{ B } +\cos ^{ 2 }{ B } =1\\ \Rightarrow \sin ^{ 2 }{ B } +{ \left( \frac { 1 }{ 3 } \right) }^{ 2 }=1\\ \Rightarrow \sin ^{ 2 }{ B } +\frac { 1 }{ 9 } =1\\ \Rightarrow \sin ^{ 2 }{ B } =1-\frac { 1 }{ 9 } =\frac { 9-1 }{ 9 } =\frac { 8 }{ 9 } \\ \Rightarrow \sin { B } =\pm \frac { 2\sqrt { 2 } }{ 3 } \\ \Rightarrow \sin { B } =\frac { 2\sqrt { 2 } }{ 3 }$ [B न्यून कोण है]

$\tan { B } =\frac { \sin { B } }{ \cos { B } } \\ \Rightarrow \tan { B } =\frac { \frac { 2\sqrt { 2 } }{ 3 } }{ \frac { 1 }{ 3 } } \\ \Rightarrow \tan { B } =2\sqrt { 2 } \\ \cot { B } =\frac { 1 }{ \tan { B } } \\ \Rightarrow \cot { B } =\frac { 1 }{ 2\sqrt { 2 } } \\ cosecB=\frac { 1 }{ \sin { B } } \\ \Rightarrow cosecB=\frac { 1 }{ \frac { 2\sqrt { 2 } }{ 3 } } \\ \Rightarrow cosecB=\frac { 3 }{ 2\sqrt { 2 } } \\ \sec { B } =\frac { 1 }{ \cos { B } } \\ \Rightarrow \sec { B } =\frac { 1 }{ \frac { 1 }{ 3 } } \\ \Rightarrow \sec { B } =3\\ \sin { B } =\frac { 2\sqrt { 2 } }{ 3 } ,\tan { B } =2\sqrt { 2 } ,\cot { B } =\frac { 1 }{ 2\sqrt { 2 } } ,\sec { B } =3,cosecB=\frac { 3 }{ 2\sqrt { 2 } }$
Example-5.यदि $\tan { A } =\sqrt { 2 } -1$ हो तो सिद्ध कीजिए कि $\sin { A } \cos { A } =\frac { 1 }{ 2\sqrt { 2 } }$
Solution-$\tan { A } =\sqrt { 2 } -1\\ 1+\tan ^{ 2 }{ A } =\sec ^{ 2 }{ A } \\ \Rightarrow 1+{ (\sqrt { 2 } -1) }^{ 2 }=\sec ^{ 2 }{ A } \\ \Rightarrow 1+2-2\sqrt { 2 } +1=\sec ^{ 2 }{ A } \\ \Rightarrow 4-2\sqrt { 2 } =\sec ^{ 2 }{ A } \\ \Rightarrow 2\sqrt { 2 } (\sqrt { 2 } -1)=\sec ^{ 2 }{ A } \\ \Rightarrow \sec { A } =\sqrt { 2\sqrt { 2 } (\sqrt { 2 } -1) } \\ \cos { A } =\frac { 1 }{ \sec { A } } \\ \cos { A } =\frac { 1 }{ \sqrt { 2\sqrt { 2 } (\sqrt { 2 } -1) } } \\ \sin ^{ 2 }{ A } +\cos ^{ 2 }{ A } =1\\ \sin ^{ 2 }{ A } +{ (\frac { 1 }{ \sqrt { 2\sqrt { 2 } (\sqrt { 2 } -1) } } ) }^{ 2 }=1\\ \Rightarrow \sin ^{ 2 }{ A } +\frac { 1 }{ 2\sqrt { 2 } (\sqrt { 2 } -1) } =1\\ \Rightarrow \sin ^{ 2 }{ A } =1-\frac { 1 }{ 2\sqrt { 2 } (\sqrt { 2 } -1) } \\ \Rightarrow \sin ^{ 2 }{ A } =\frac { 2\sqrt { 2 } (\sqrt { 2 } -1)-1 }{ 2\sqrt { 2 } (\sqrt { 2 } -1) } \\ \Rightarrow \sin ^{ 2 }{ A } =\frac { 4-2\sqrt { 2 } -1 }{ 2\sqrt { 2 } (\sqrt { 2 } -1) } \\ \Rightarrow \sin ^{ 2 }{ A } =\frac { 3-2\sqrt { 2 } }{ 2\sqrt { 2 } (\sqrt { 2 } -1) } \\ \Rightarrow \sin ^{ 2 }{ A } =\frac { { (\sqrt { 2 } -1) }^{ 2 } }{ 2\sqrt { 2 } (\sqrt { 2 } -1) } \\ \Rightarrow \sin ^{ 2 }{ A } =\frac { { (\sqrt { 2 } -1) } }{ 2\sqrt { 2 } } \\ \Rightarrow \sin { A } =\sqrt { \frac { { (\sqrt { 2 } -1) } }{ 2\sqrt { 2 } } } \\ \sin { A } \cos { A } =\sqrt { \frac { { (\sqrt { 2 } -1) } }{ 2\sqrt { 2 } } } .\frac { 1 }{ \sqrt { 2\sqrt { 2 } (\sqrt { 2 } -1) } } \\ \Rightarrow \sin { A } \cos { A } =\frac { 1 }{ 2\sqrt { 2 } }$
Example-6.यदि $\tan { A } =2$ हो तो $\sec { A } \sin { A } +\tan ^{ 2 }{ A } -cosecA$ का मान ज्ञात कीजिए।
Solution-$\tan { A } =2\\ 1+\tan ^{ 2 }{ A } =\sec ^{ 2 }{ A } \\ \Rightarrow 1+{ (2) }^{ 2 }=\sec ^{ 2 }{ A } \\ \Rightarrow 1+4=\sec ^{ 2 }{ A } \\ \Rightarrow \sec ^{ 2 }{ A } =5\\ \Rightarrow \sec { A } =\sqrt { 5 } \\ \cos { A } =\frac { 1 }{ \sec { A } } \\ \Rightarrow \cos { A } =\frac { 1 }{ \sqrt { 5 } } \\ \sin ^{ 2 }{ A } +\cos ^{ 2 }{ A } =1\\ \Rightarrow \sin ^{ 2 }{ A } +{ (\frac { 1 }{ \sqrt { 5 } } ) }^{ 2 }=1\\ \Rightarrow \sin ^{ 2 }{ A } +\frac { 1 }{ 5 } =1\\ \Rightarrow \sin ^{ 2 }{ A } =1-\frac { 1 }{ 5 } \\ \Rightarrow \sin ^{ 2 }{ A } =\frac { 5-1 }{ 5 } \\ \Rightarrow \sin ^{ 2 }{ A } =\frac { 4 }{ 5 } \\ \Rightarrow \sin { A } =\frac { 2 }{ \sqrt { 5 } } \\ cosecA=\frac { 1 }{ \sin { A } } \\ \Rightarrow cosecA=\frac { \sqrt { 5 } }{ 2 } \\ \sec { A } \sin { A } +\tan ^{ 2 }{ A } -cosecA\\ \Rightarrow \sqrt { 5 } (\frac { 2 }{ \sqrt { 5 } } )+{ (2) }^{ 2 }-\frac { \sqrt { 5 } }{ 2 } \\ \Rightarrow 2+4-\frac { \sqrt { 5 } }{ 2 } \\ \Rightarrow 6-\frac { \sqrt { 5 } }{ 2 } \\ \Rightarrow \frac { 12-\sqrt { 5 } }{ 2 } \\ \sec { A } \sin { A } +\tan ^{ 2 }{ A } -cosecA=\frac { 12-\sqrt { 5 } }{ 2 }$
Example-7.यदि $\sin { \theta } =\frac { 4 }{ 5 }$  हो तो $\frac { 4\tan { \theta } -5\cos { \theta } }{ \sec { \theta } +4\cot { \theta } }$  का मान ज्ञात कीजिए।
Solution-$\sin { \theta } =\frac { 4 }{ 5 } \\ \sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } =1\\ \Rightarrow { (\frac { 4 }{ 5 } ) }^{ 2 }+\cos ^{ 2 }{ \theta } =1\\ \Rightarrow \frac { 16 }{ 25 } +\cos ^{ 2 }{ \theta } =1\\ \Rightarrow \cos ^{ 2 }{ \theta } =1-\frac { 16 }{ 25 } \\ \Rightarrow \cos ^{ 2 }{ \theta } =\frac { 25-16 }{ 25 } \\ \Rightarrow \cos { \theta } =\frac { 9 }{ 25 } \\ \sec { \theta } =\frac { 1 }{ \cos { \theta } } \\ \Rightarrow \sec { \theta } =\frac { 5 }{ 3 } \\ \tan { \theta } =\frac { \sin { \theta } }{ \cos { \theta } } \\ \Rightarrow \tan { \theta } =\frac { \frac { 4 }{ 5 } }{ \frac { 3 }{ 5 } } \\ \Rightarrow \tan { \theta } =\frac { 4 }{ 3 } \\ \cot { \theta } =\frac { 1 }{ \tan { \theta } } \\ \Rightarrow \cot { \theta } =\frac { 3 }{ 4 } \\ \frac { 4\tan { \theta } -5\cos { \theta } }{ \sec { \theta } +4\cot { \theta } } \\ =\frac { 4(\frac { 4 }{ 3 } )-5(\frac { 3 }{ 5 } ) }{ \frac { 5 }{ 3 } +4(\frac { 3 }{ 4 } ) } \\ =\frac { \frac { 16 }{ 3 } -\frac { 3 }{ 1 } }{ \frac { 5 }{ 3 } +\frac { 3 }{ 1 } } \\ =\frac { \frac { 16-9 }{ 3 } }{ \frac { 5+9 }{ 3 } } \\ =\frac { 7 }{ 14 } \\ \frac { 4\tan { \theta } -5\cos { \theta } }{ \sec { \theta } +4\cot { \theta } } =\frac { 1 }{ 2 }$
Example-8.यदि $\sin { \theta } =\frac { { a }^{ 2 }-{ b }^{ 2 } }{ { a }^{ 2 }+{ b }^{ 2 } }$  हो तो $\cos { \theta }$  और $\tan { \theta }$ के मान त्रिकोणमितीय अनुपातों में परस्पर सम्बन्धों की सहायता से ज्ञात कीजिए। $\theta$  न्यून कोण है।
(If it is $\sin { \theta } =\frac { { a }^{ 2 }-{ b }^{ 2 } }{ { a }^{ 2 }+{ b }^{ 2 } }$, find the values ​​of $\cos { \theta }$ and $\tan { \theta }$ with the help of Relation Between Trigonometric Ratios. The $\theta$ is acute angle.)

Solution:-$\sin { \theta } =\frac { { a }^{ 2 }-{ b }^{ 2 } }{ { a }^{ 2 }+{ b }^{ 2 } } \\ \sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } =1\\ \Rightarrow \cos ^{ 2 }{ \theta } =1-\sin ^{ 2 }{ \theta } \\ \Rightarrow \cos ^{ 2 }{ \theta } =1-{ (\frac { { a }^{ 2 }-{ b }^{ 2 } }{ { a }^{ 2 }+{ b }^{ 2 } } ) }^{ 2 }\\ \Rightarrow \cos ^{ 2 }{ \theta } =\frac { { ({ a }^{ 2 }+{ b }^{ 2 }) }^{ 2 }-{ ({ a }^{ 2 }-{ b }^{ 2 }) }^{ 2 } }{ { ({ a }^{ 2 }+{ b }^{ 2 }) }^{ 2 } } \\ \Rightarrow \cos ^{ 2 }{ \theta } =\frac { { a }^{ 4 }+{ b }^{ 4 }+2{ a }^{ 2 }{ b }^{ 2 }-{ a }^{ 4 }-{ b }^{ 4 }+2{ a }^{ 2 }{ b }^{ 2 } }{ { ({ a }^{ 2 }+{ b }^{ 2 }) }^{ 2 } } \\ \Rightarrow \cos ^{ 2 }{ \theta } =\frac { 4{ a }^{ 2 }{ b }^{ 2 } }{ { ({ a }^{ 2 }+{ b }^{ 2 }) }^{ 2 } } \\ \Rightarrow \cos { \theta } =\pm \frac { 2ab }{ { ({ a }^{ 2 }+{ b }^{ 2 }) } } \\ \Rightarrow \cos { \theta } =\frac { 2ab }{ { ({ a }^{ 2 }+{ b }^{ 2 }) } }$($\theta$ न्यून कोण है)

$\tan { \theta } =\frac { \sin { \theta } }{ \cos { \theta } } \\ \tan { \theta } =\frac { \frac { { a }^{ 2 }-{ b }^{ 2 } }{ { a }^{ 2 }+{ b }^{ 2 } } }{ \frac { 2ab }{ { ({ a }^{ 2 }+{ b }^{ 2 }) } } } \\ \Rightarrow \tan { \theta } =\frac { { a }^{ 2 }-{ b }^{ 2 } }{ 2ab }$
उपर्युक्त उदाहरणों के द्वारा त्रिकोणमितीय अनुपातों में परस्पर सम्बन्ध (Relation Between Trigonometric Ratios) को समझ सकते हैं।

3.त्रिकोणमितीय अनुपातों में परस्पर सम्बन्ध की समस्याएं (Relation Between Trigonometric Ratios Problems)-

(1.)यदि $\sin { A } =\frac { 5 }{ 13 }$  हो तो $\cos { A }$  और $\tan { A }$  का मान ज्ञात कीजिए।
(2.)यदि $\cos { \theta } =\frac { 1 }{ \sqrt { 2 } }$  हो तो $\sin { \theta }$  और $\cot { \theta }$  का मान ज्ञात कीजिए।
(3.)यदि $\sec { \theta } =2$ तो $\tan { \theta }  ,\cos { \theta }$ तथा  $\sin { \theta }$ का मान ज्ञात कीजिए।
(4.)यदि $\tan { \theta } =\sqrt { 3 }$  हो तो शेष त्रिकोणमितीय अनुपातों को त्रिकोणमितीय अनुपातों में परस्पर सम्बन्धों (Relation Between Trigonometric Ratios) की सहायता से ज्ञात कीजिए जबकि $\theta$ एक न्यून कोण है।
(5.)यदि $cosecA=\sqrt { 10 }$ हो तो $\cot { A } ,\sin A,\cos { A }$ परस्पर सम्बन्धों (Relation Between Trigonometric Ratios) की सहायता से ज्ञात कीजिए जबकि $\theta$ एक न्यून कोण है।

(6)यदि $\cot { \theta } =\frac { 1 }{ \sqrt { 3 } }$ हो तो सिद्ध कीजिए।

$\frac { 1-\cos ^{ 2 }{ \theta } }{ 2-\sin ^{ 2 }{ \theta } } =\frac { 3 }{ 5 }$

• उत्तर-$(1)\cos { A } =\frac { 12 }{ 13 } ,\tan { A } =\frac { 5 }{ 12 } \\ (2)\sin { \theta } =\frac { 1 }{ \sqrt { 2 } } ,\cot { \theta } =1\\ (3)\cos { \theta } =\frac { 1 }{ 2 } ,\sin { \theta } =\frac { \sqrt { 3 } }{ 2 } ,\tan { \theta } =\sqrt { 3 } \\ (4)\sec { \theta } =2,\cos { \theta } =\frac { 1 }{ 2 } \\ \sin { \theta } =\frac { \sqrt { 3 } }{ 2 } ,cosec\theta =\frac { 2 }{ \sqrt { 3 } } \\ \cot { \theta } =\frac { 1 }{ \sqrt { 3 } } \\ (5)\cot { A } =3,\sin { A } =\frac { 1 }{ \sqrt { 10 } } \\ \cos { A } =\frac { 3 }{ \sqrt { 10 } }$
• उपर्युक्त सवालों को हल करने पर त्रिकोणमितीय अनुपातों में परस्पर सम्बन्ध (Relation Between Trigonometric Ratios) को ठीक से समझा जा सकता है।

4.त्रिकोणमिति का अनुपात क्या है? (What is the ratio of trigonometry?),SEC के लिए अनुपात क्या है? (What is the ratio for SEC?)-

Sin θ=Opposite Side to θ/Hypotenuse
Cos θ=Adjacent Side to θ/Hypotenuse
Tan θ =Opposite Side/Adjacent Side & Sin θ/Cos θ
Cot θ =Adjacent Side/Opposite Side & 1/tan θ
Sec θ =Hypotenuse/Adjacent Side & 1/cos θ
Cosec θ= Hypotenuse/Opposite Side & 1/sin θ

• नोट: विपरीत भुजा लंबवत भुजा है और आसन्न भुजा त्रिभुज का आधार है।इसके अलावा, इन अनुपातों या प्रत्येक त्रिकोणमितीय फलनों के बारे में विस्तार से जानने के लिए त्रिकोणमितीय फ़ंक्शन देखें।
  परिभाषा
• त्रिकोणमितीय अनुपातों को एक समकोण त्रिभुज में भुजाओं के अनुपात के मूल्य के आधार पर सभी त्रिकोणमितीय फलनों के मान के रूप में परिभाषित किया गया है।अपने किसी भी न्यून कोण के संबंध में समकोण त्रिभुज की भुजाओं के अनुपात को उस विशेष कोण के त्रिकोणमितीय अनुपात के रूप में जाना जाता है।
• समकोण त्रिभुज की तीन भुजाएँ हैं:
  हाइपोटेन्यूज़ (सबसे लंबी भुजा)
  लंब (कोण के विपरीत)
  आधार (कोण के समीप)

5. क्या त्रिकोणमितीय अनुपात होना संभव है? (Is it possible to have a trigonometric ratios?)-

• छह त्रिकोणमितीय अनुपात, sin, cos, tan, cosecant, secant और cotangent हैं।इन्हें भुजाओं के अनुपात के रूप में संदर्भित किया जाता है क्योंकि इन्हें एक विशिष्ट कोण θ के लिए समकोण त्रिभुज की भुजाओं के रूप में व्यक्त किया जा सकता है।

6.त्रिकोणमितीय अनुपात और उनके संबंध (Trigonometric ratios and their relations)-

• छह त्रिकोणमितीय अनुपात, sine,cosine,tangent, cosecant, secant and cotangent हैं।इन छह त्रिकोणमितीय अनुपातों को sin, cos, tan, cosec, sec, cot के रूप में संक्षिप्त किया जाता है।इन्हें अनुपात के रूप में संदर्भित किया जाता है क्योंकि इन्हें एक विशिष्ट कोण θ के लिए समकोण त्रिभुज की भुजाओं के अनुपात के रूप में व्यक्त किया जा सकता है।

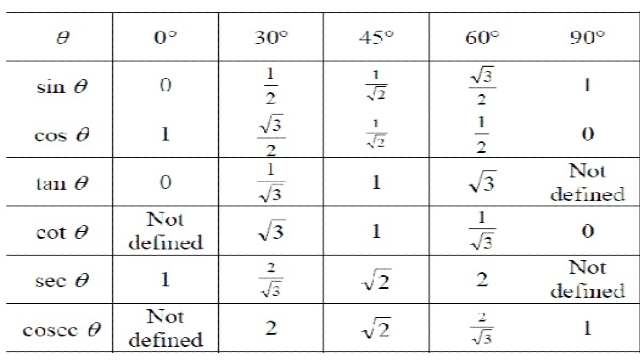
7.त्रिकोणमिति सारणी (Trigonometry table)-

नीचे त्रिकोणमितीय कोणों के मानों की सारणी दी गई है।

8.त्रिकोणमिति के व्युत्क्रम संबंध (Reciprocal relations of trigonometry)-

• त्रिकोणमितीय अनुपातों के व्युत्क्रम संबंधों को यहां तीन जोड़े त्रिकोणमितीय अनुपातों के साथ-साथ उनके व्युत्क्रम संबंधों के बीच प्रदर्शित करने के लिए समझाया गया है। बता दें कि समकोण त्रिभुज में कोण OMP ,M पर समकोण है।sinθ और cosecθ एक दूसरे के व्युत्क्रम हैं। cosθ और secθ एक दूसरे के व्युत्क्रम हैं।इसी प्रकार tanθ तथा cotθ एक दूसरे के व्युत्क्रम हैं।

9.त्रिकोणमितीय अनुपात के वर्ग संबंध (Square relations of trigonometric ratios)-

• त्रिकोणमितीय अनुपात के वर्ग संबंध नीचे दिए गए हैं-
  (1) sin² θ + cos² θ = 1.
  (2) sec² θ - tan² θ = 1.
  (3) cosec² θ - cot² θ = 1.

10.त्रिकोणमिति में भागफल संबंध (Quotient relations in trigonometry)-

• त्रिकोणमितीय अनुपात के भागफल संबंध (Quotient relations of trigonometric ratios) हैं $tanθ=\frac { sinθ }{ cosθ }$ और $cotθ=\frac { cosθ }{ sinθ }$
  समकोण त्रिभुज OMP जो M पर समकोण है तथा ∠MOP = θ.
  उपर्युक्त उदाहरणों, सवालों तथा प्रश्नों के उत्तर द्वारा त्रिकोणमितीय अनुपातों में परस्पर सम्बन्ध (Relation Between Trigonometric Ratios), को समझ सकते हैं।

Also Read This Article:-Trigonometric functions of two angles

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here