Types of Relations in Discrete Maths
1.विविक्त गणित में सम्बन्धों के प्रकार (Types of Relations in Discrete Maths),सम्बन्धों के प्रकार (Types of Relations):
विविक्त गणित में सम्बन्धों के प्रकार (Types of Relations in Discrete Maths) के इस आर्टिकल में सार्वत्रिक ,तत्समक ,स्वतुल्य,सममित,प्रतिसममित,संक्रामक और तुल्यता सम्बन्ध के बारे में अध्ययन करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Relation in Discrete Mathematics
2.विविक्त गणित में सम्बन्धों के प्रकार के साधित उदाहरण (Types of Relations in Discrete Maths Solved Illustrations):
Illustration:1.माना A={1,2,3,4} तथा
(Let A={1,2,3} and}
R_1=\{(1,1),(2,2),(3,3)\} \\ R_2=\{(1,1),(1,2),(1,3),(3,1),(3,3),(4,4)\} \\ R_3=\phi \\ R_4=\{(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3), (2,4) ,(3,1), \\ (3,2),(3,3),(3,4), (4,1),(4,2),(4,3),(4,4)\} \\ R_5=\{(1,1),(1,2),(2,1),(2,2),(3,3),(3,4),(4,3),(4,4)\} \\ R_6=\{(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)\} \\ R_7=\{(1,3),(2,2),(2,4),(3,1),(4,2)\}
A पर परिभाषित सम्बन्ध हैं।तब बताइए कि कौन-कौनसे सम्बन्ध स्वतुल्य,सममित,प्रतिसममित या संक्रामक हैं?
(be the relations on A. Then determine which of the relations are reflexive,symmetric,antisymmetric or transitive?)
Solution: R_1=\{(1,1),(2,2),(3,3)\}
सममित तथा प्रतिसममित है।
R_2=\{(1,1),(1,2),(1,3),(3,1),(3,3),(4,4)\}
स्वतुल्य,सममित,प्रतिसममित तथा संक्रामक में से कोई भी सम्बन्ध नहीं है।
R_3=\phi , स्वतुल्य सम्बन्ध नहीं है।
R_4=\{(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3), \\(3,4),(4,1),(4,2),(4,3),(4,4)\}
स्वतुल्य,सममित तथा संक्रामक सम्बन्ध है।
R_5=\{(1,1),(1,2),(2,1),(2,2),(3,3),(3,4), (4,3),(4,4)\}
स्वतुल्य,सममित तथा संक्रामक सम्बन्ध है।
R_6=\{(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)\}
प्रतिसममित तथा संक्रामक सम्बन्ध है।
R_7=\{(1,3),(2,2),(2,4),(3,1),(4,2)\}
सममित सम्बन्ध है।
Illustration:2.एक ऐसे सम्बन्ध का उदाहरण दीजिए जो
(i)सममित है।
(ii)न तो सममित है और न ही प्रतिसममित है।
(Give an example of a relation which is:
(i)symmetric
(ii)antisymmetric.)
Solution: (i) R_1=\{(1,1),(2,2),(3,3),(4,4)\}
(ii) R_2=\{(1,3),(1,4),(2,4),(3,1),(3,4)\}
Illustration:3.बताइए कि सम्बन्ध R जिसका आव्यूह M_R निम्नलिखित हैं,स्वतुल्य,सममित,प्रतिसममित तथा संक्रामक है अथवा नहीं?
(Determine, whether matrix the relation R,whose matrix M_R is given below is reflexive,symmetric,antisymmetric and (or) transitive or not?)
Illustration:3(i). M_R=\left[\begin{array}{llll} 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \end{array}\right]
Solution: M_R=\left[\begin{array}{llll} 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \end{array}\right] \\ M_R=\{(1,1),(1,2),(1,4),(2,3), (2,4),(3,2),(4,1),(4,2)\}
स्वतुल्य,सममित,प्रतिसममित तथा संक्रामक सम्बन्ध नहीं है।
Illustration:3(ii). M_R=\left[\begin{array}{llll} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]
Solution: M_R=\left[\begin{array}{llll} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] \\ M_R=\{(1,1),(1,2),(2,1),(2,2),(3,3),(4,4)\}
स्वतुल्य,सममित तथा संक्रामक सम्बन्ध है।
Illustration:3(iii). M_R=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]
Solution: M_R=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] \\ M_R=\{(1, 1),(2,2),(2,3),(3,2),(3,3),(4,4)\}
स्वतुल्य,सममित तथा संक्रामक है।
Illustration:4.यदि A सभी अशून्य पूर्णांकों का समुच्चय है तथा "\approx" समुच्चय A×A पर
(a, b) \approx (c, d) \Leftrightarrow a d=b c ; a, b, c, d \in A द्वारा परिभाषित कोई सम्बन्ध है तब सिद्ध कीजिए कि एक तुल्यता सम्बन्ध है।
(Set A be the set of all non zero integers,and let be a relation on A×A defined by (a, b) \approx (c, d) \Leftrightarrow a d=b c ; a, b, c, d \in A . Then show that "\approx" is an equivalence relation on A×A.)
Solution:माना a \in A
तब a \in I \Rightarrow a a \approx a a \Leftrightarrow a^2 = a^2 \\ \Rightarrow (a, a) \in R
अतः R स्वतुल्य है।
माना (a d, b c) \in R जहाँ a,b,c,d \in A
तब (a d, b c) \in R \Rightarrow a d \approx b c \Leftrightarrow a d=b c \\ \Rightarrow b c=a d \left[ \because a, b \in I \Rightarrow a \cdot b=b \cdot a \right] \\ \Rightarrow b c \approx a d \\ \Rightarrow (b c, a d) \in R
\therefore R सममित है।
अब माना कि (ad,bc),(b c, e f) \in R जहाँ a , b , c, d ,e ,f \in A
तब (ad, bc) \in R \Rightarrow a d \approx b c \Leftrightarrow a d=b c तथा (b c, e f) \in R \Rightarrow b c \approx e f \Leftrightarrow b c=e f \\ \Rightarrow a d=e f \\ \Rightarrow a d \approx e f \\ \Rightarrow a d \approx e f \in R
अतः R संक्रामक है।
फलतः "\approx" एक तुल्यता सम्बन्ध है।
Illustration:5.यदि R,समुच्चय A पर कोई सम्बन्ध है तथा,तत्समकी सम्बन्ध है तो सिद्ध कीजिए
(If R is a relation on the set A and is the identity relation then show that):
I_A o R=R=R o I_A
Solution:माना (a, a),(b, b) \in I_A तथा (a, b) \in R
a, b \in A तब संयुक्त फलन की परिभाषा से
(a, b) \in I_{A} o R
तथा (a, b) \in R o I_A
अतः I_A o R=R=R o I_A
Illustration:6.निम्न कथन के समर्थन में उदाहरण दीजिए:
(i)यदि R संक्रामक है तो R \cap R^{-1} रिक्त हो सकता है।
(ii)यदि R प्रतिसममित है तो R \cap R^{-1} रिक्त हो सकता है।
(Give an example to support the following statements:
(i)If R is a transitive relation then R \cap R^{-1} may be empty.
(ii)If R is an antisymmetric relation then R \cap R^{-1} may be empty.)
Solution:(i).माना R={(a,b),(b,c),(a,c)} संक्रामक सम्बन्ध है तब
R^{-1}=\{(b, a),(c, b),(c, a)\} \\ R \cap R^{-1}=\phi
(ii).माना R={(a,b)}
प्रतिसममित सम्बन्ध है तब
R^{-1}=\{(b, a)\} \\ R \cap R^{-1}=\phi
Illustration:7.यदि R तथा S,समुच्चय A पर तुल्यता सम्बन्ध है तो क्या संयुक्त सम्बन्ध SoR भी A पर तुल्यता सम्बन्ध है?
(If R and S are equivalence relations on a set A. Is the composite relation SoR an equivalence relation on A?):
Solution:चूँकि R तथा S,A पर तुल्यता सम्बन्ध है।
(i).R तथा S,स्वतुल्य सम्बन्ध है।
\forall a \in A,(a, a) \in R तथा (a, a) \in S\\ \Rightarrow(a, a) \in R o S \forall a \in A
\Rightarrow SoR, A पर एक स्वतुल्य सम्बन्ध है।
(ii).R तथा S सममित सम्बन्ध है
\forall a, b, c, d \in A,(a, b),(b, a) \in R तथा (c, d), (d, c) \in S \\ \Rightarrow \phi \in S o R \forall a, b, c, d \in A
\Rightarrow RoS, A पर एक सममित नहीं सम्बन्ध है।
(iii)R तथा S संक्रामक सम्बन्ध है
\forall a, b, c, d, e, f \in A,(a, b),(b, c), (a, c) \in R
तथा (d, e),(e, f),(d, f) \in S \\ \Rightarrow \phi \in R o S \forall a, b, c, d, e, f \in A
\Rightarrow SoR, A पर एक संक्रामक सम्बन्ध नहीं है।
अतः संयुक्त सम्बन्ध SoR तुल्यता सम्बन्ध नहीं है।
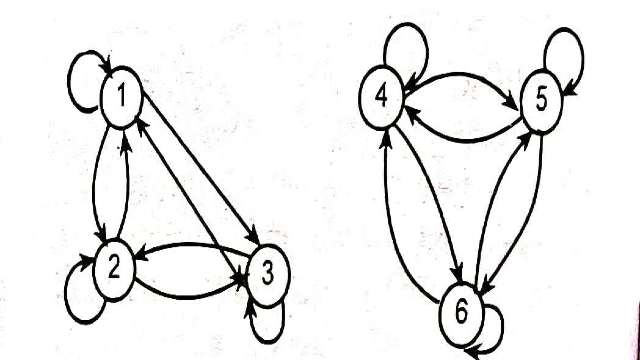
Illustration:8.समुच्चय A={1,2,3,4,5,6} पर किसी सम्बन्ध R का दिष्ट ग्राफ निम्न प्रकार है:
(The directed graph of the relation R on the set A={1,2,3,4,5,6} is):
बताइए कि सम्बन्ध R एक तुल्यता सम्बन्ध है अथवा नहीं।
(Determine whether the relation R on A is an equivalence relation or not?):
Solution:दिए हुए दिष्ट ग्राफ द्वारा समुच्चय A={1,2,3,4,5,6} पर परिभाषित सम्बन्ध R है:
R={(1,1),(1,2),(2,1),(2,2),(1,3),(3,1),(2,3),(3,2),(4,4),(4,5),(5,4),(4,6),(6,4),(5,6),(6,5)}
स्पष्टतः उपर्युक्त सम्बन्ध R स्वतुल्य है।
चूँकि (1,2) \in R तथा (2,1) \in R[/katex]
अतः सम्बन्ध R सममित है।
इसी प्रकार (1,2),(2,3) \in R \Rightarrow (1,3) \in R
अतः R संक्रामक सम्बन्ध भी है।
फलतः R तुल्यता सम्बन्ध है।
उपर्युक्त उदाहरणों के द्वारा विविक्त गणित में सम्बन्धों के प्रकार (Types of Relations in Discrete Maths),सम्बन्धों के प्रकार (Types of Relations) को समझ सकते हैं।
3.विविक्त गणित में सम्बन्धों के प्रकार की समस्याएँ (Types of Relations in Discrete Maths Problems):
(1.)मान लीजिए I पूर्णांकों के संबंध का समुच्चय है। I पर संबंध R को निम्नानुसार परिभाषित करें: xRy यदि और केवल यदि x-y,5 से विभाज्य है। तथा \forall x, y \in I
दर्शाइए कि R,I पर एक तुल्यता संबंध है।
(Let I be the set of relation of integers.Define a relation R on I as follows:xRy if and only if x-y is divisible by 5,\forall x, y \in I . )
Show that R is an equivalence relation on I.
(2.)दर्शाइए कि पूर्णांकों के समुच्चय m पर सर्वांगसमता मापांक m का संबंध तुल्यता मापांक m है।
(Show that the relation of congruence modulo m on the set I of integers is an equivalence modulo m.)
उपर्युक्त सवालों को हल करने पर विविक्त गणित में सम्बन्धों के प्रकार (Types of Relations in Discrete Maths),सम्बन्धों के प्रकार (Types of Relations) को ठीक से समझ सकते हैं।
4.सम्बन्धों के प्रकार और उनकी परिभाषा (Types of Relations and Their Definition):
(1.)रिक्त सम्बन्ध (Empty Relation or Void Relation):माना A और B दो अरिक्त समुच्चय हैं।तब उप समुच्चय \phi \subset A \times B ,A से B में एक रिक्त सम्बन्ध (Empty relation) कहलाता है।
(2.)सार्वत्रिक सम्बन्ध (Universal relation):माना A तथा B दो अरिक्त समुच्चय हैं।तब समुच्चय A×B स्वयं का एक उपसमुच्चय है तथा इसे सार्वत्रिक सम्बन्ध (universal relation) कहते हैं।
(3.)तत्समक सम्बन्ध (Identity relation):माना A एक अरिक्त समुच्चय है।तब A×A का उपसमुच्चय I_{A}=\{ (a,a); a \in A\} ,समुच्चय A पर तत्समक सम्बन्ध कहलाता है।
तत्समक सम्बन्ध को समानता सम्बन्ध (Relation of equality) या विकर्ण सम्बन्ध (diagonal relation) भी कहते हैं।
(4.)स्वतुल्य सम्बन्ध (Reflexive relation):अरिक्त समुच्चय A पर परिभाषित सम्बन्ध R एक स्वतुल्य सम्बन्ध कहलाता है यदि प्रत्येक a \in A के लिए (a,a) \in R
अतः समुच्चय A पर कोई सम्बन्ध R एक स्वतुल्य सम्बन्ध कहलाता है यदि समुच्चय A का प्रत्येक अवयव स्वयं से सम्बन्धित है।
अरिक्त समुच्चय A पर परिभाषित तत्समक सम्बन्ध सदैव स्वतुल्य होता है।परन्तु A पर प्रत्येक स्वतुल्य सम्बन्ध,तत्समक सम्बन्ध नहीं होता।जैसे कि A={1,2,3} पर परिभाषित सम्बन्ध R={(1,1),(1,2),(2,2),(3,2),(3,3)} स्वतुल्य तो है परन्तु तत्समक सम्बन्ध नहीं।
(5.)सममित सम्बन्ध (Symmetric Relation):अरिक्त समुच्चय A पर परिभाषित सम्बन्ध R, एक सममित सम्बन्ध कहलाता है यदि a,b \in A के लिए (a,b) \in R \Rightarrow (b,a) \in R अर्थात् a R b \Rightarrow b R a;a,b \in A
(6.)संक्रामक सम्बन्ध (Transitive relation):अरिक्त समुच्चय A पर परिभाषित कोई सम्बन्ध R,एक संक्रामक सम्बन्ध कहलाता है यदि a,b,c \in A के लिए
(a,b) \in R तथा (b,c) \in R \Rightarrow (a,c) \in R
अर्थात् aRb तथा bRc \Rightarrow aRc ; a,b,c \in A
(7.)प्रतिसममित सम्बन्ध (Antisymmetric Relation):अरिक्त समुच्चय A पर परिभाषित कोई सम्बन्ध R एक प्रतिसममित सम्बन्ध कहलाता है यदि a,b \in A के लिए (a,b) \in R तथा (b,a) \in R \Rightarrow a=b
(8.)तुल्यता सम्बन्ध (Equivalence Relation):
समुच्चय A पर सम्बन्ध R एक तुल्यता सम्बन्ध है यदि
(i) (a,a) \in R \forall a \in A
(ii) (a,b) \in R \Rightarrow (b,a) \in R ;a ,b \in A तथा
(iii) (a,b) \in R तथा (b,c) \in R \Rightarrow (a,c) \in R ; a,b,c \in A
Also Read This Article:- Composite Relation in Discrete Maths
5.विविक्त गणित में सम्बन्धों के प्रकार (Frequently Asked Questions Related to Types of Relations in Discrete Maths),सम्बन्धों के प्रकार (Types of Relations) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.क्या सार्वत्रिक सम्बन्ध सदैव स्वतुल्य होता है? (Is a Universal Relation Always Reflexive?):
उत्तर:अरिक्त समुच्चय A पर परिभाषित सार्वत्रिक सम्बन्ध सदैव स्वतुल्य होता है।
प्रश्न:2.क्या प्रतिसममिति और सममिति परस्पर विलोम हैं? (Are Antisymmetry and Symmetry Opposite?):
उत्तर:यदि (a, b) \in R(a \neq b) परन्तु (b, a) \notin R ,तो भी R समुच्चय A पर एक प्रतिसममित सम्बन्ध है अर्थात् सम्बन्ध R एक प्रतिसममित सम्बन्ध है यदि और केवल समुच्चय A के दो भिन्न-भिन्न अवयव a और b इस प्रकार नहीं है कि a, b से सम्बन्धित है तथा b,a से सम्बन्धित है “सममिति” तथा “प्रतिसममिति” परस्पर विलोम नहीं है चूँकि कोई भी सम्बन्ध R,दोनों सममित तथा प्रतिसममित हो सकता है तथा नहीं भी।
प्रश्न:3.तुल्यता सम्बन्ध से क्या आशय है? (What Do You Mean by Equivalence Relation?):
उत्तर:अरिक्त समुच्चय A पर परिभाषित कोई सम्बन्ध R, एक तुल्यता सम्बन्ध कहलाता है यदि यह स्वतुल्य,सममित तथा संक्रामक है।
उपर्युक्त प्रश्नों के उत्तर द्वारा विविक्त गणित में सम्बन्धों के प्रकार (Types of Relations in Discrete Maths),सम्बन्धों के प्रकार (Types of Relations) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here | |
| 7. | click here |
Types of Relations in Discrete Maths
विविक्त गणित में सम्बन्धों के प्रकार
(Types of Relations in Discrete Maths)
Types of Relations in Discrete Maths
विविक्त गणित में सम्बन्धों के प्रकार (Types of Relations in Discrete Maths) के इस
आर्टिकल में सार्वत्रिक ,तत्समक ,स्वतुल्य,सममित,प्रतिसममित,संक्रामक और तुल्यता सम्बन्ध
के बारे में अध्ययन करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.