Relative Velocity in Dynamics
1.गतिविज्ञान में आपेक्षिक वेग (Relative Velocity in Dynamics),आपेक्षिक वेग तथा त्वरण (Relative Velocity and Acceleration):
गतिविज्ञान में आपेक्षिक वेग (Relative Velocity in Dynamics) के इस आर्टिकल में दो गतिमान कणों में एक कण का दूसरे कण के सापेक्ष वेग और त्वरण तथा कोण ज्ञात करने के बारे में अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Velocity and Acceleration in Dynamics
2.गतिविज्ञान में आपेक्षिक वेग पर आधारित उदाहरण (Examples Based on Relative Velocity in Dynamics):
Example:2.उत्तर-पूर्व की ओर जाते हुए एक मनुष्य को हवा,उत्तर से बहती हुई मालूम पड़ती है,किन्तु वह जब अपनी चाल दुगुनी करता है तो हवा उत्तर से \cot^{-1} 2 पूर्व की ओर आती हुई मालूम पड़ती है।सिद्ध करो कि हवा की वास्तविक दिशा पूर्व की ओर है।
(A person travelling towards the north-east finds that the wind appears to blow from the north but when he doubles his speed it seems to come from a direction inclined at angle \cot^{-1} 2 on the east of north. Prove that the true direction of the wind is towards the east.)
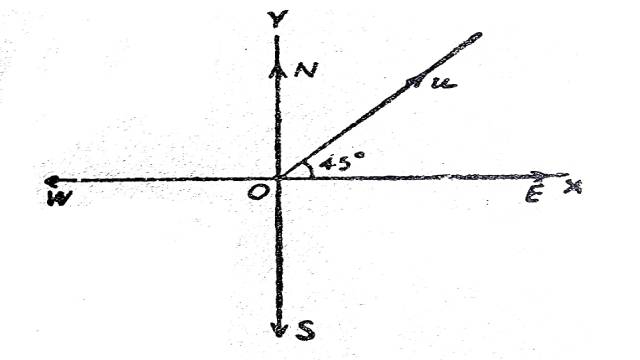
Solution:माना उत्तर-पूर्व में व्यक्ति का वेग u है,इसका OX और OY की दिशा में घटक क्रमशः u \cos 45^{\circ}=\frac{u}{\sqrt{2}} तथा u \sin 45^{\circ}=\frac{u}{\sqrt{2}} है।
पुनः माना हवा का वास्तविक वेग v है जो OX के साथ कोण \alpha बनाती है इसलिए इसके OX व OY दिशा की तरफ वास्तविक घटक क्रमशः v \cos \alpha और v \sin \alpha हैं।अब माना कि हवा जो OX के साथ कोण \theta बनाती है,व्यक्ति के सापेक्ष हवा का वेग V है।
प्रथम स्थिति:हवा का किसी दिशा में व्यक्ति के सापेक्ष वेग=हवा का वास्तविक वेग-व्यक्ति का उस दिशा में वेग
V \cos \theta=v \cos \alpha-\frac{u}{\sqrt{2}} तथा V \sin \theta=v \sin \alpha-\frac{u}{\sqrt{2}}
\because हवा उत्तर से आती हुई मालूम पड़ती है \theta=90^{\circ} \\ \therefore v \cos \alpha=\frac{u}{\sqrt{2}}\left(\because \cos 90^{\circ}=0\right) \cdots(1)
स्थिति द्वितीय:व्यक्ति का वेग 2u हो जाता है इसलिए OX तथा OY की दिशा में घटक क्रमशः
2 u \cos 45^{\circ}=u \sqrt{2} तथा 2 \sin 45^{\circ}= u \sqrt{2} \\ v \cos \theta=v \cos \alpha- u \sqrt{2} =\frac{u}{ \sqrt{2}}-u \sqrt{2}=-u \sqrt{2} [(1) से]
तथा V \sin \theta=v \sin \alpha-u \sqrt{2} \\ \therefore \tan \theta=\frac{v \sin \alpha-u \sqrt{2}}{-u \sqrt{2}} \cdots(2) \\ \phi=\cot^{-1} 2 \Rightarrow \cot \phi=2 \text { तथा } \theta=90-\phi \\ \tan \theta=\tan (90-\phi)=\cot \phi=2
(2) सेः -\frac{u}{\sqrt{2}} \cdot 2=(v \sin \alpha-u \sqrt{2}) \\ \Rightarrow v \sin \alpha=0 \cdots(3)
हवा का परिणामी वास्तविक वेग
=\sqrt{(v \cos \alpha)^2+(v \sin \alpha)^2}=\frac{u}{\sqrt{2}}
तथा \tan \alpha=0 [(1) और (3) से]
\therefore \alpha=0 अतः हवा की वास्तविक दिशा पूर्व है।
Example:3.पूर्व की ओर 2 km. प्रति घंटे की चाल से चलने वाले किसी मनुष्य को हवा सीधा उत्तर से आती हुई मालूम पड़ती है।जब वह अपनी चाल को दुगुना कर लेता है तो हवा उसे उत्तर-पूर्व से आती मालूम पड़ती है।हवा के वास्तविक वेग का परिणाम एवं दिशा ज्ञात कीजिए।
(A person travelling towards east with a speed of 2 km/hr finds that the wind appears to blow from the north.When he doubles his speed it seems to come from north-east. Find the true magnitude and direction of the wind.)
Solution:उत्तर की ओर व्यक्ति का वेग 2km/hr है,इसका OX और OY की दिशा में घटक क्रमशः 2 तथा शून्य होगा।
माना हवा का वास्तविक वेग v है जो OX के साथ कोण \alpha बनाती है इसलिए इसके OX व OY दिशा की तरफ वास्तविक घटक क्रमशः v \cos \alpha और v \sin \alpha हैं।अब माना कि व्यक्ति के सापेक्ष हवा का सापेक्ष वेग V है जो OX-अक्ष के साथ कोण \theta बनाती है।
प्रथम स्थिति:हवा का किसी दिशा में व्यक्ति के सापेक्ष वेग=हवा का वास्तविक वेग-व्यक्ति का उस दिशा में वेग
V \cos \theta=v \sin \alpha-2 तथा V \sin \theta=v \sin \alpha-0 \\ V \cos 90^{\circ}=v \cos \alpha-2 तथा V \sin 90^{\circ}=v \sin \alpha [हवा उत्तर से आ रही है अतः \theta=\sin 90^{\circ} ]
2=v \cos \alpha तथा V=v \sin \alpha \cdots(1)
वर्ग करके जोड़ने पर
v^2 \cos ^2 \alpha+v^2 \sin ^2 \alpha=4+V^2 \\ \Rightarrow v^2=V^2+4 \Rightarrow V^2=v^2-4 \cdots(2)
स्थिति द्वितीय:व्यक्ति का वेग दुगुना हो जाता है इसलिए OX तथा OY की दिशा में घटक क्रमशः 4 \cos 0=4 तथा 4 \sin 0=0 हैं।
V \cos \theta=v \cos \alpha-4=2-4 [(1) से]
V \cos \theta=-2 तथा V \sin \theta=v \sin \alpha-0
\theta=45^{\circ} रखने परः
V \cos 45^{\circ}=-2 तथा V \sin 45^{\circ}=v \sin \alpha
\Rightarrow \frac{V}{\sqrt{2}}=-2 तथा \frac{V}{\sqrt{2}}=v \sin \alpha \\ \Rightarrow v \sin \alpha=-2 \cdots(3)
(1) और (3) सेःV=-2
V का मान (2) में रखने परः
(-2)^2=v^2-4 \Rightarrow v^2=4+4 \\ \Rightarrow v^2=8 \Rightarrow v=2 \sqrt{2}
v का मान समीकरण (3) में रखने परः
2 \sqrt{2} \sin \alpha=-2 \\ \sin \alpha=-\frac{1}{\sqrt{2}} \\ \Rightarrow \sin \alpha=-\sin 45^{\circ} \\ \Rightarrow \sin \alpha=\sin \left(180^{\circ}+45^{\circ}\right) \Rightarrow \alpha=225^{\circ}
हवा पश्चिम-दक्षिण से बह रही है।वास्तविक वेग v=2 \sqrt{2} km /hr.
Example:4.3 किमी/घण्टे की चाल से टहलते हुए एक मनुष्य को वर्षा का जल सीधा उर्ध्वाधर दिशा में गिरता हुआ मालूम पड़ता है।जब वह अपना वेग 4 किमी/घण्टा कर लेता है तो क्षैतिज के साथ 60° का कोण गिरते हुए मालूम पड़ता है।सिद्ध कीजिए कि वर्षा की वास्तविक दिशा क्षैतिज के साथ 30° कोण बनाती है।
(To a man walking at the rate of 3 km/hr the rain appears to fall vertically.When he increases his speed to 4 km/hr, it appears to meet him at angle 60° with the horizon. Show that the real direction of the rain is 30° with the horizon.)
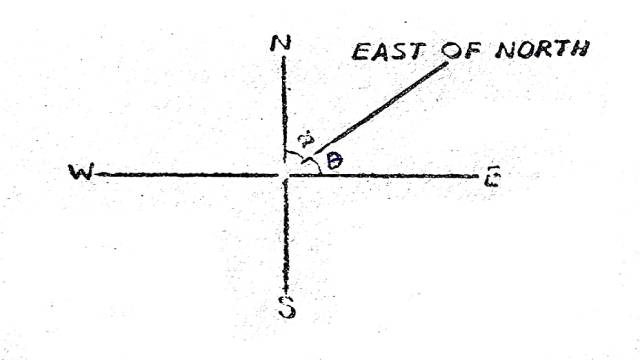
Solution:माना वर्षा का जल किसी समय \theta कोण बनाता है।वर्षा का वास्तविक वेग v है तथा वर्षा का वास्तविक कोण क्षैतिज के साथ \beta है।मनुष्य क्षैतिज के साथ \alpha कोण बनाता है।
जब \theta=90^{\circ} (वर्षा का जल उर्ध्वाधर गिरता प्रतीत होता है)
u=3 \mathrm{~km} / \mathrm{hr}, \alpha=0 (मनुष्य द्वारा क्षैतिज के साथ कोण)
\tan \theta=\frac{v \sin \beta-u \sin \alpha}{v \cos \beta-u \cos \alpha} \\ \tan 90^{\circ}=\frac{v \sin \beta-3 \sin 0^{\circ}}{v \cos \beta-3 \cos 0^{\circ}}\\ \Rightarrow \infty=\frac{v \sin \beta-3 \times 0}{v \cos \beta-3 \times 1} \\ \Rightarrow \frac{1}{0}=\frac{v \sin \beta-3 \times 0}{v \cos \beta-3 } \left[ \because \infty =\frac{1}{0} \right] \\ \Rightarrow v \cos \beta=3 \cdots(1)
पुनः \theta=-60^{\circ} (ऋणात्मक दिशा में) , \alpha=0^{\circ}, u=4
\tan \left(-60^{\circ}\right)=\frac{v \sin \beta-4 \sin 0^{\circ}}{v \cos \beta-4 \cos 0^{\circ}} \\ \Rightarrow - \sqrt{3}=\frac{v \sin \beta-4 \times 0}{v \cos \beta-4 \times 1} \\ -\sqrt{3}(v \cos \beta-4)=v \sin \beta \\ \Rightarrow -\sqrt{3} v \cos \beta+4 \sqrt{3}=\sin \beta \\ \Rightarrow v \sin \beta+\sqrt{3} v \cos \beta=4 \sqrt{3} \\ \Rightarrow v(\sin \beta+\sqrt{3} \cos \beta)=4 \sqrt{3} \cdots(2)
समीकरण (2) में (1) का भाग देने परः
\frac{v(\sin \beta+\sqrt{3} \cos \beta)}{v \cos \beta}=\frac{4 \sqrt{3}}{3} \\ \Rightarrow \frac{\sin \beta+\sqrt{3} \cos \beta}{\cos \beta}=\frac{4}{\sqrt{3}} \\ \Rightarrow \sqrt{3} \sin \beta+3 \cos \beta=4 \cos \beta \\ \Rightarrow \sqrt{3} \sin \beta-\cos \beta \\ \Rightarrow \tan \beta=\frac{1}{\sqrt{3}} \\ \Rightarrow \tan \beta=\tan 30^{\circ} \\ \Rightarrow \beta=30^{\circ}
Example:5.एक जहाज उत्तर की ओर 12 km/hr के वेग से जाता हुआ अपने से पूर्व की ओर तथा 10 km दूर,एक दूसरे जहाज को जाते हुए देखता है।दूसरा जहाज पश्चिम की ओर 16 km/hr के वेग से जा रहा है।कितने समय बाद वे दूसरे से कम से कम दूरी पर है और वह कम से कम दूरी क्या है?
(A ship steaming north at the rate of 12 km.p.h observes a ship, due east of itself distant 10 km, which is steaming due west at the rate of 16 km/hr. After what time are they at the least distance from one another and what is this least distance?):
Solution:दूसरे जहाज के लिए
x=10-16t
प्रथम जहाज के लिए
y=12t
दोनों जहाजों के बीच दूरी
z=\sqrt{x^2+y^2} \\ =\sqrt{(10-16 t)^2+(12 t)^2} \\ \Rightarrow z =\sqrt{100-320 t+256 t^2+144 t^2} \cdots(1) \\ \Rightarrow z^2=100-320 t+400 t^2
t के सापेक्ष अवकलन करने पर:
2 z \frac{d z}{d t}=-320+800 t
न्यूनतम दूरी के लिए
\frac{d z}{d t}=0 \\ -320+800 t=0 \\ \Rightarrow t=\frac{320}{800}=\frac{2}{5} hr
\Rightarrow t=\frac{2}{5} \times 60=24 min
t का मान समीकरण (1) में रखने परः
z =\sqrt{100-320 \times \frac{2}{5}+400 \times\left(\frac{2}{5}\right)^2} \\ =\sqrt{\left(100-128+400 \times \frac{4}{25}\right)} \\ =\sqrt{-28+64} \\ \Rightarrow z=\sqrt{36}
z=6 km तथा t=24 minutes
Example:6.ABC एक समकोण त्रिभुज है जिसका कोण C समकोण है।A तथा B से एक ही समय दो कण C की ओर BC तथा AC के समानुपातिक वेग से चलना प्रारम्भ करते हैं।सिद्ध करो कि उनके बीच निम्नतम दूरी \frac{\left(A C^2-B C^2\right)}{A B} .
(ABC is a triangle,right angled at C. Points starts from A and B at the same time and move towards C with velocities proportional to BC and AC. Show that their least distance is \frac{\left(A C^2-B C^2\right)}{A B} .)
Solution:दिया है कि AC की तरफ वेग kBC तथा BC की तरफ वेग kAC है।
A से C की तरफ चलने वाले कण के लिए
x=AC-kBC.t
तथा B से C की ओर चलने वाले कण के लिए
y=BC-kAC.t
\triangle ABC समकोण त्रिभुज है अतः
AB^2=AC^2+BC^2 \cdots(1)
किसी समय t पर A व B के बीच दूरी z=\sqrt{x^2+y^2} \\ \Rightarrow z=\sqrt{(AC-K \quad \text{BC} t)^2+(\text{BC} -K \quad \text{AC} t)^2} \cdots(2) \\ \Rightarrow z^2=(\text{AC}-K \quad \text{BC} t)^2+( \text{BC}-K \quad \text{AC} t)^2
t के सापेक्ष अवकलन करने परः
\Rightarrow 2 z \frac{d z}{d t}=2(\text{AC}-K \quad \text{BC} t)(-K \quad \text{BC})+2(\text{BC}-K \quad \text{AC} \cdot t)(-K \text{AC}) \\ \Rightarrow z \frac{d z}{d t}=-K \quad \text{BC}(\text{AC}-K \quad \text{BC} \cdot t)-K \quad \text{AC}(\text{BC}-K \quad \text{AC} \cdot t)
न्यूनतम दूरी के लिए \frac{d z}{d t}=0\\ =K \text{BC}(\text{AC}-k \text{BC} \cdot t)-K \text{AC}(\text{BC}-K \text{BC} \cdot t)=0 \\ \Rightarrow-K\left[\text{AC} \quad \text{BC}-K \text{BC}^2 \cdot t+\text{AC} \cdot \text{BC}-K \text{AC}^2 \cdot t\right]=0 \\ \Rightarrow 2 \text{AC} \quad \text{BC}-K \text{BC}^2 \cdot t-K \text{AC}^2 \cdot t=0 \\ \Rightarrow K t\left(B C^2+A C^2\right)=2 \text{AC} \cdot \text{BC} \\ t=\frac{2 A C \cdot B C}{K\left(B C^2+A C^2\right)} \cdots(3)
t का मान समीकरण (3) से (2) में रखने परः
z=\sqrt{\left[AC-\frac{K BC \cdot 2 AC \cdot B C}{K\left(B C^2+A C^2\right)}\right]^2+\left[BC-\frac{K A C \cdot 2 AC \cdot BC}{K\left(B C^2+A C^2\right)}\right]^2} \\ =\sqrt{ \frac{\left(A C^3+AC \cdot B C^2-2 A C \cdot B C^2\right)^2+\left(B C^3+B C \cdot A C^2-2 AC^2 \cdot B C\right)^2}{\left(B C^2+A C^2 \right)^2}} \\ =\frac{\sqrt{\left(A C^3-A C \cdot B C^2\right)^2+\left(B C^3- A C^2 \cdot BC^2\right)^2}}{B C^2+A C^2} \\ =\frac{\sqrt{A C^2\left(A C^2-B C^2\right)^2+\left(B C^2-A C^2\right)^2 \cdot B C^2}}{B C^2+A C^2} \\ =\frac{\sqrt{A C^2\left(A C^2-B C^2\right)^2+\left(A C^2-B C^2\right)^2-B C^2}}{B C^2+A C^2} [ \because(a-b)^2=(b-a)^2 से ]
=\frac{\sqrt{\left(A C^2-B C^2\right)^2 \cdot\left(A C^2+B C^2\right)}}{B C^2+A C^2} \\=\frac{\left(A C^2-B C^2\right) \sqrt{\left(A C^2+B C^2\right)}}{A C^2+B C^2} \\ =\frac{\left(A C^2-B C^2\right)}{\sqrt{A C^2+B C^2}} \\ =\frac{\left(A C^2-B C^2\right)}{\sqrt{A B^2}} [समीकरण (1) से]
\Rightarrow z=\frac{\left(A C^2-B C^2\right)}{A B}
Example:7.नदी के एक किनारे पर स्थित बिन्दु A से दूसरे किनारे पर स्थित बिन्दु B तक सीधी रेखा से जाने में 10 मिनट लगते हैं जबकि लौटने में 20 मिनट लगते हैं।धारा का वेग 3 कि.मी. प्रति घण्टा है तथा धारा के सापेक्ष नाव का वेग 6 कि.मी. प्रति घण्टा है।नदी की चौड़ाई और धारा की दिशा में A से B की दूरी ज्ञात करो।
(A boat takes 10 minutes to cross a river in a straight line from a point A on one bank to a point B on the other and 20 minutes to do the return journey. The current flows at 3 km per hour and the velocity of the boat relative to the current is 6 km per hour. Find the width of the river and the down stream distance from A and B.)
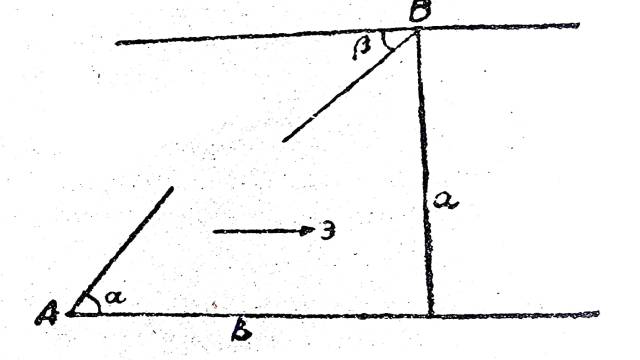
Solution:प्रथम स्थिति:नाव का धारा की दिशा में वास्तविक वेग=नाव का सापेक्ष वेग+धारा का वास्तविक वेग
\therefore V \cos \theta=6 \cos \alpha+3
तथा V \sin \theta=6 \sin \alpha
नाव 10 मिनट का समय लेती है अतः
10 मिनट=\frac{10}{60}=\frac{1}{6} घण्टे
(6 \cos \alpha+3) \times \frac{1}{6}=b \Rightarrow \cos \alpha=b-\frac{1}{2}
तथा 6 \sin \alpha \times \frac{1}{6}=a \Rightarrow \sin \alpha=a
वर्ग करके जोड़ने परः
a^2+\left(b-\frac{1}{2}\right)^2=\sin ^2 \alpha+\cos ^2 \alpha \\ \Rightarrow a^2+\left(b-\frac{1}{2}\right)^2=1 \cdots(1)
द्वितीय स्थिति:
V \cos \phi=6 \cos \beta-3 तथा V \sin \phi=6 \sin \beta
अब 20 मिनट समय लेती है अतः 20 मिनट=20 \times \frac{1}{60} =\frac{1}{3} घण्टे
\therefore(6 \cos \beta-3) \times \frac{1}{3}=b \Rightarrow \cos \beta=\frac{1}{2}(b+1)
तथा 6 \sin \beta \times \frac{1}{2}=a \Rightarrow \sin \beta=\frac{a}{2}
वर्ग करके जोड़ने परः
\sin ^2 \beta+\cos ^2 \beta=\frac{a^2}{4}+\frac{1}{4}(b+1)^2 \\ \Rightarrow a^2+(b+1)^2=4 \ldots(2)
(2) में से (1) घटाने परः
(b+1)^2-\left(b-\frac{1}{2}\right)^2=3 \\ \Rightarrow 2 b+1+b-\frac{1}{4}=3 \Rightarrow 3 b=\frac{9}{4} \\ \Rightarrow b=\frac{3}{4}
b का मान (1) में रखने परः
a^2+\left(\frac{3}{4}-\frac{1}{2}\right)^2=1 \Rightarrow a^2=1-\frac{1}{16} \\ \Rightarrow a=\frac{\sqrt{15}}{4}, b=\frac{3}{4}
Example:8.दो सीधी सड़कें OX तथा OY परस्पर न्यूनकोण \alpha बनाती है,एक गाड़ी u वेग से OX के अनुदिश चलती है,तथा दूसरी v वेग से OY के अनुदिश चलती है।सिद्ध करो कि जब गाड़ियाँ एक-दूसरे के निकटतम हों, तो O से उनकी दूरियों का अनुपात \frac{v+u \cos \alpha}{u+v \cos \alpha} होगा।जब दूसरी गाड़ी O पर है और यदि प्रथम गाड़ी O से d पर हो,तो सिद्ध करो कि गाड़ियाँ \frac{d(u+v \cos \alpha)}{u^2+v^2+2 u v \cos \alpha} समय पश्चात एक-दूसरे से निकटतम होंगी।
(Two straight roads OX, and OY are inclined to each other at an acute angle \alpha , one car moves along OX with speed u while a second car moves along OY with speed v;show that when the cares are at the least distance apart,the ratio of their distance from O is \frac{v+u \cos \alpha}{u+v \cos \alpha}. If the first car is at a distance d from O when the second is at O.Show that the cars at their least distance apart after time \frac{d(u+v \cos \alpha)}{u^2+v^2+2 u v \cos \alpha}.)
Solution:t समय के बाद दोनों गाड़ियों की स्थिति क्रमशः A’ व B’ है।
अतः O A^{\prime}=a-u t तथा O B^{\prime}=v t
और \angle A^{\prime} O B^{\prime}=\alpha \\ \therefore\left(A^{\prime} B^{\prime}\right)^2=(a-u t)^2+v^2 t^2-2(a-u t) v t \cos \alpha [त्रिकोणमिति के सूत्र से]
=\left(u^2+v^2+2 u v \cos \alpha\right) t^2-(2 a u+2 a v \cos \alpha) \cdot t + a^2
A’B’ न्यूनतम होगा जब \frac{d}{d t}\left(A^{\prime} B^{\prime}\right)^2=0 \\ 2 t\left(u^2+v^2+2 u v \cos \alpha\right)-2(a u+a v \cos \alpha)=0 \\ \therefore t=\frac{a(u+v \cos \alpha)}{u^2+v^2+2 u v \cos \alpha} \cdots(1)
\frac{OA'}{OB'} जहाँ A’ और B’,t समय बाद A व B की स्थिति है:
\frac{a-u t}{v t}=\frac{a}{v t}-\frac{u}{v} \\=a \cdot \frac{u^2+v^2+2 u v \cos \alpha}{v a(u+v \cos \alpha)}-\frac{u}{v}=\frac{v+u \cos \alpha}{u+v \cos \alpha} [(1) से]
उपर्युक्त उदाहरणों के द्वारा गतिविज्ञान में आपेक्षिक वेग (Relative Velocity in Dynamics),आपेक्षिक वेग तथा त्वरण (Relative Velocity and Acceleration) को समझ सकते हैं।
3.गतिविज्ञान में आपेक्षिक वेग पर आधारित सवाल (Questions Based on Relative Velocity in Dynamics):
(1.)एक जहाज एक सीधी रेखा के साथ एक स्थिर गति v पर प्रवाहित होता है,जबकि एक अन्य पोत एक स्थिर गति V पर भाप लेता है,पहला हमेशा एक बीम रखता है,यह दर्शाइए कि किसी भी पोत का पथ दूसरे के अपेक्षाकृत शंक्वाकार खंड की उत्केन्द्रता \frac{v}{V} है।
(A vessel streams at a constant speed v along a straight line,whilst another vessel steaming at a constant speed V,keeps the first always exactly a beam, show that the path of either vessel relatively to the other is a conic section of eccentricity \frac{v}{V}.)
(2.)दो बिंदु P और Q एक ही बिंदु से एक साथ चलते हैं और एक वृत्त में और एक सीधी रेखा में समान रूप से चलता हैं जो वृत्त को छूता है, प्रत्येक की चाल v है।P का Q के सापेक्ष पथ और सापेक्ष वेग ज्ञात करो।
(Two points P and Q start simultaneously from the same point and moves uniformly in a circle and in a straight line which touches the circle, each with a speed v.Find the path of P with respect to Q and the relative velocity.)
(2.) x=a \sin \theta-a \theta , y=a(1-\cos \theta)
Relative velocity =2 v \sin \frac{\theta}{2}, x के साथ कोण \phi=\frac{\pi}{2}+\frac{\theta}{2}
उपर्युक्त सवालों को हल करने पर गतिविज्ञान में आपेक्षिक वेग (Relative Velocity in Dynamics),आपेक्षिक वेग तथा त्वरण (Relative Velocity and Acceleration) को ठीक से समझ सकते हैं।
Also Read This Article:- Motion of a Particle in a Plane
4.गतिविज्ञान में आपेक्षिक वेग (Frequently Asked Questions Related to Relative Velocity in Dynamics),आपेक्षिक वेग तथा त्वरण (Relative Velocity and Acceleration) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.आपेक्षिक वेग को स्पष्ट करो। (Explain the Relative Velocity):
उत्तर:जब दो गतिमान कणों A और B के बीच दूरी परिणाम (magnitude) या दिशा (direction) या दोनों बदलते हैं तो प्रत्येक कण दूसरे के सापेक्ष आपेक्षिक वेग से गतिमान कहलाएगा।कण B का A के सापेक्ष आपेक्षिक वेग,B का A के सापेक्ष विस्थापन की दर होती है।दूसरे शब्दों में A को विराममावस्था में मानने पर जिस वेग से B चलता हुआ दिखाई देता है उसे कण B का A के सापेक्ष आपेक्षिक वेग कहते हैं।
प्रश्न:2.आपेक्षिक वेग कैसे ज्ञात करते हैं? (How is the Relative Velocity Determined?):
उत्तर:यदि B की A के सापेक्ष आपेक्षिक स्थिति (x,y) हो,तब
x=x_2-x_1 तथा y=y_2-y_1
\therefore A के सापेक्ष B के आपेक्षिक वेगों के घटक (components) होंंगे
\dot{x}=\dot{x_2}-\dot{x_1} तथा \dot{y}=\dot{y_2}-\dot{y_1}
प्रश्न:3.आपेक्षिक त्वरण कैसे ज्ञात करते हैं? (How is the Relative Acceleration Determined?):
उत्तर:A के सापेक्ष B के आपेक्षिक त्वरणों के घटक (components) होंगे
\ddot{x}=\ddot{x_2}-\ddot{x_1} तथा \ddot{y}=\ddot{y_2}-\ddot{y_1}
किसी दिशा में A का B के सापेक्ष आपेक्षिक वेग (या त्वरण)=उसी दिशा में B का वास्तविक वेग (या त्वरण)+A के वेग (या त्वरण) के बराबर विपरीत दिशा में।
प्रश्न:4.आपेक्षिक कोणीय वेग ज्ञात करने का सूत्र लिखो। (Write the Formula for Finding the Relative Angular Velocity):
उत्तर:B का A के सापेक्ष आपेक्षिक कोणीय वेग=\frac{v \sin \beta-u \sin \alpha}{AB}
A तथा B के वेग क्रमशः u तथा v हैं जो AB (x-अक्ष के साथ) के साथ \alpha तथा \beta कोण बनाते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा गतिविज्ञान में आपेक्षिक वेग (Relative Velocity in Dynamics),आपेक्षिक वेग तथा त्वरण (Relative Velocity and Acceleration) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here | |
| 7. | click here |
(Relative Velocity in Dynamics)
गतिविज्ञान में आपेक्षिक वेग
(Relative Velocity in Dynamics)
(Relative Velocity in Dynamics)
गतिविज्ञान में आपेक्षिक वेग (Relative Velocity in Dynamics) के इस आर्टिकल में दो
गतिमान कणों में एक कण का दूसरे कण के सापेक्ष वेग और त्वरण तथा कोण ज्ञात करने के
बारे में अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.