Relation in Discrete Mathematics
1.विविक्त गणित में सम्बन्ध (Relation in Discrete Mathematics),सम्बन्ध (Relation):
विविक्त गणित में सम्बन्ध (Relation in Discrete Mathematics) के इस आर्टिकल में सम्बन्ध का परिसर,प्रान्त,प्रतिलोम सम्बन्ध,दिष्ट ग्राफ आदि ज्ञात करने वाले सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Mathematical Induction Discrete Maths
2.विविक्त गणित में सम्बन्ध के उदाहरण (Relation in Discrete Mathematics Examples):
Example:1.यदि समुच्चय A={1,2,3,4} से समुच्चय B={a,b,c} में कोई सम्बन्ध R, “R={(1,a),(1,c),(2,a),(2,b),(3,a),(3,b)}” द्वारा परिभाषित है।तब ज्ञात कीजिए:
(If R is a relation from the set A={1,2,3,4} to the set B={a,b,c} given by “R={(1,a),(1,c),(2,a),(2,b),(3,a),(3,b)}”.Then find):
Example:1(i).R का प्रान्त (domain of R),
Solution:R का प्रान्त={1,2,3}
Example:1(ii).R का परिसर (range of R),
Solution:R का परिसर={a,b,c}
Example:1(iii).R का प्रतिलोम सम्बन्ध (inverse relation of R),
Solution:R का प्रतिलोम सम्बन्ध
R^{-1}={(a,1),(c,1),(a,2),(b,2),(a,3),(b,3)}
Example:2.यदि समुच्चय A={1,2,3,4,5,6} पर कोई सम्बन्ध R निम्नलिखित रूप से परिभाषित है।”xRy यदि और केवल यदि x,y का गुणक है” तब ज्ञात कीजिए:
(If R is a relation on the set A={1,2,3,4,5,6} defined by “xRy if and only if x is a multiple of y”.Then find):
Example:2(i).R का प्रान्त (domain of R)
Solution:R={(1,1),(2,1),(3,1),(4,1),(5,1),(6,1),(2,2),(4,2),(6,2),(3,3),(6,3),(4,4),(5,5),(6,6)}
R का प्रान्त={1,2,3,4,5,6}
Example:2(ii).R का परिसर (Range of R)
Solution:R का परिसर={1,2,3,4,5,6}
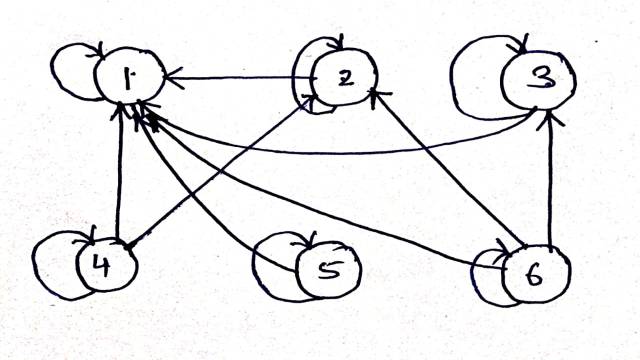
Example:2(iii).R का दिष्ट ग्राफ (directed graph of R)
Solution:R का दिष्ट ग्राफ निम्न है:
Example:3.यदि R समुच्चय A={1,2,3,4,5,8} पर कोई सम्बन्ध है जो “xRy यदि और केवल यदि x+y< 9 “द्वारा परिभाषित है,तो ज्ञात कीजिए:
(If R is a relation on the set A={1,2,3,4,5,8} defined by “xRy if and only if x+y< 9 ” ;then find):
Example:3(i).R का प्रान्त (domain of R),
Solution:R={1,1),(1,2),(1,3),(1,4),(1,5),(2,1),(2,2),(2,3),(2,4),(2,5),(3,1),(3,2),(3,3),(3,4),(3,5),(4,1),(4,2),(4,3),(4,4),(5,1),(5,2),(5,3)}
R का प्रान्त={1,2,3,4,5}
Example:3(ii).R का परिसर (range of R),
Solution:R का परिसर={1,2,3,4,5}
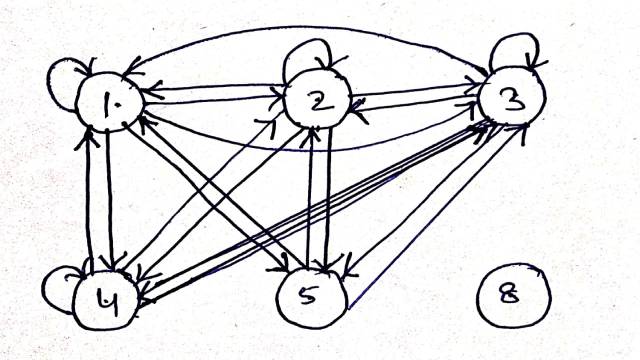
Example:3(iii).R का दिष्ट ग्राफ (directed graph of R)
Solution:R का दिष्ट ग्राफ
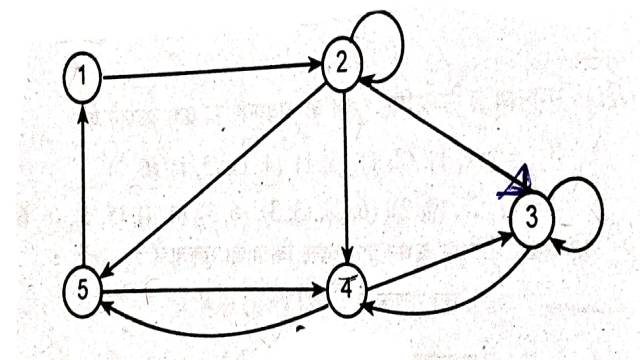
Example:4.निम्न दिष्ट ग्राफ द्वारा निर्धारित सम्बन्ध R को ज्ञात कीजिए:
(Find the relation R determined by):
Solution:R={(2,2),(3,3),(1,2),(5,1),(2,5),(5,4),(4,5),(4,3),(3,4),(2,3),(2,4)}
Example:5.यदि समुच्चय A={1,2,3,4,5} पर कोई सम्बन्ध R “xRy यदि और केवल यदि x-y,3 से विभाजित है” द्वारा परिभाषित है [i.e. , x \equiv y (mod 3)]।तब ज्ञात कीजिए।
(If R is a relation on the set A={1,2,3,4,5} defined by “xRy if and only if x-y is divisible by 3” [i.e. , x \equiv y (mod 3)] .Then find):
Example:5(i). R तथा R^{-1} ( R and R^{-1} )
Solution:R={(1,1),(1,4),(2,2),(2,5),(3,3),(4,1),(5,2),(4,4),(5,5)}
R^{-1}={(1,1),(4,1),(2,2),(5,2),(3,3),(1,4),(2,5),(4,4),(5,5)}
Example:5(ii).R तथा R^{-1} के प्रान्त (domain of R and R^{-1}),
Solution:R का प्रान्त={1,2,3,4,5}
R^{-1} का प्रान्त={1,2,3,4,5}
Example:7.यदि R तथा S समुच्चय A पर सम्बन्ध है तो सिद्ध कीजिए कि,
(If R and S are relations on the set A,then prove that):
Example:7(i). R \subseteq S \Rightarrow R^{-1} \subseteq S^{-1}
Solution: R \subseteq S \Rightarrow R^{-1} \subseteq S^{-1}
माना R \subseteq S \quad \forall(x, y) \in R तथा
R^{-1}=(y, x) \\ (x, y) \in R \Rightarrow(x, y) \in S \\ \Rightarrow (y, x) \in S^{-1} \\ \Rightarrow R^{-1} \subseteq S^{-1} \\ \Rightarrow R \subseteq S \Rightarrow R^{-1} \subseteq S^{-1}
Example:7(ii). R \subseteq S \Rightarrow \bar{S} \subseteq \bar{R}
Solution: R \subseteq S \Rightarrow \bar{S} \subseteq \bar{R}
माना A={x,y} अतः A×A={(x,x),(y,y),(x,y),(y,x)}
माना R={(x,x}}
तथा S=\{(x,x),(x,y)\} \left[ \therefore R \subseteq S \right] \\ \bar{R}=\{(y, y),(x, y),(y, x)\} \cdots(1)
तथा \bar{S}=\{(y, y),(y, x)\} \cdots(2) \\ \Rightarrow \bar{S} \subseteq \bar{R}
अतः R \subseteq S \Rightarrow \bar{S} \subseteq \bar{R}
Example:7(iii). (R \cup S)^{-1}=\bar{R}^{-1} \cup S^{-1}
Solution: (R \cup S)^{-1}=\bar{R}^{-1} \cup S^{-1}
माना R=\{(x, x)\}, S=\{(x, y)\} \\ R \cup S=\{(x, x),(x, y)\} \\ (R \cup S)^{-1}=\{(x, x),(y, x)\} \cdots(1) \\ R^{-1}=\{(x, x)\} तथा S^{-1}=\{(y, x)\} \cdots(1)\\ R^{-1} \cup S^{-1}=\{(x, x),(y, x)\} \cdots(2)
(1) व (2) सेः
(R \cup S)^{-1}=R^{-1} \cup S^{-1}
Example:7(iv). (R \cap S)^{-1}=R^{-1} \cap S^{-1}
Solution: (R \cap S)^{-1}=R^{-1} \cap S^{-1}
माना R={(x,x),(x,y)}
तथा S={(x,y),(y,x)}
R \cap S=\{(x, y)\} \\ (R \cap S)^{-1}=\{(y, x)\} \cdots(1) \\ R^{-1}=\{(x, x),(y, x)\} \\ S^{-1}=\{(y, x),(x, y)\} \\ R^{-1} \cap S^{-1}=\{(y, x)\}
(1) व (2) सेः
(R \cap S)^{-1}=R^{-1} \cap S^{-1}
उपर्युक्त उदाहरणों के द्वारा विविक्त गणित में सम्बन्ध ,सम्बन्ध (Relation) को समझ सकते हैं।
3.विविक्त गणित में सम्बन्ध के सवाल (Relation in Discrete Mathematics Questions):
(1.)यदि A={1,2,3} तथा B={p,q} हो,तो
R_1={(1,p),(2,q),(3,q)}
R_2={(1,p),(q,2)}
उपर्युक्त में से कौन-सा सम्बन्ध है?
(2.)यदि A={1,2,3,4} तथा B=\{\alpha, \beta, \gamma\} तथा R=\{(2, \alpha),(4, \alpha),(4, \beta)\} तो R का प्रान्त और परिसर ज्ञात कीजिए।
उत्तर (Answers):(1.) R_{1} सम्बन्ध है तथा R_2 सम्बन्ध नहीं है।
(2.)R का प्रान्त={2,4}
R का परिसर=\{\alpha, \beta\}
उपर्युक्त सवालों को हल करने पर विविक्त गणित में सम्बन्ध ,सम्बन्ध (Relation) को ठीक से समझ सकते हैं।
Also Read This Article:- Sets and Propositions
4.विविक्त गणित में सम्बन्ध (Frequently Asked Questions Related to Relation in Discrete Mathematics),सम्बन्ध (Relation) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.क्रमित समुच्चय किसे कहते हैं? (What is a Ordered Set?):
उत्तर:दो अवयवों का ऐसा समुच्चय जिसमें सुनिश्चित रूप से एक अवयव को उसका प्रथम सदस्य तथा दूसरे अवयव को उसका दूसरा सदस्य लिया जाता है इसी आधार पर उन दोनों में भेद किया जा सकता है।उदाहरणार्थ,यदि a,b दो सदस्य हों तो (a,b) एक क्रमित युग्म दिग्दर्शित करता है जिसमें a पहला सदस्य है तथा b दूसरा सदस्य है।
प्रश्न:2.द्विआधारी सम्बन्ध को परिभाषित कीजिए। (Define Binary Relation):
उत्तर:माना A तथा B कोई दो अरिक्त समुच्चय हैं।तब कार्तीय गुणनफल A×B का कोई भी उपसमुच्चय A से B में एक द्विआधारी सम्बन्ध (binary relation) (या सम्बन्ध) कहलाता है।दूसरे शब्दों में समुच्चय A से B में कोई सम्बन्ध A×B के क्रमित युग्मों (a,b) का एक समुच्चय R है,जहाँ (a,b) का प्रथम अवयव a,समुच्चय A का तथा द्वितीय अवयव b,समुच्चय B का अवयव है।यदि क्रमित युग्म (a,b) समुच्चय R का अवयव है तो इसे हम a R b द्वारा निरूपित करते हैं तथा “a,b से सम्बन्धित है” पढ़ते हैं।इसी प्रकार यदि (a,b), R का अवयव नहीं है तो इसे हम a \not R b द्वारा निरूपित करते हैं।स्पष्ट है कि R \subseteq A \times B
प्रश्न:3.सम्बन्ध का दिष्ट ग्राफ के रूप में निरूपण कैसे करते हैं? (How is the Representation of a Relation in the Form of a Directed Graph?):
उत्तर:परिमित समुच्चय A पर परिभाषित किसी सम्बन्ध R को दिष्ट ग्राफ के द्वारा भी दर्शाया जा सकता है।इसके लिए सर्वप्रथम हम समुच्चय A के प्रत्येक अवयव के संगत लघुवृत्त की रचना करते हैं तथा प्रत्येक वृत्त को संगत अवयव से नामित कर देते हैं।इन वृत्तों को हम शीर्ष (vertices) कहते हैं।अब हम शीर्ष a_{i} को शीर्ष a_{j} से एक तीर (arrow) द्वारा सम्बद्ध करते हैं यदि और केवल यदि अवयव a_{i} अवयव a_{j} से सम्बन्धित है,i.e. यदि और केवल यदि \left(a_i, a_j\right) \in R इन तीरों को हम दिष्ट कोर (directed edges) कहते हैं।इस प्रकार प्राप्त आरेख (diagram) को दिए हुए सम्बन्ध R का दिष्ट ग्राफ (directed graph or digraph) कहते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here | |
| 7. | click here |
Relation in Discrete Mathematics
विविक्त गणित में सम्बन्ध
(Relation in Discrete Mathematics)
Relation in Discrete Mathematics
विविक्त गणित में सम्बन्ध (Relation in Discrete Mathematics) के इस आर्टिकल में
सम्बन्ध का परिसर,प्रान्त,प्रतिलोम सम्बन्ध,दिष्ट ग्राफ आदि ज्ञात करने वाले सवालों को हल
करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.