Laws of Kepler for Planetary Motion
1.ग्रहों की गति के लिए केप्लर के नियम (Laws of Kepler for Planetary Motion),ग्रहों की गति के लिए केप्लर के नियम हिन्दी में (Laws of Kepler for Planetary Motion in hindi):
ग्रहों की गति के लिए केप्लर के नियम (Laws of Kepler for Planetary Motion):सुप्रसिद्ध डेनिस ज्योतिषी केप्लर (1571-1630) ने सौर परिवार के ग्रहों की गति के लिए कुछ आनुभविक निम्न नियमों का प्रतिपादन किया:
(1.)केप्लर का प्रथम नियम(Kepler’s First Law):प्रत्येक ग्रहों की कक्षाएं दीर्घवृत्त के रूप की है जिनकी एक नाभि पर सूर्य स्थित है।
(Each planet describe an ellipse with the sun as one of the foci.)
(2.)केप्लर का द्वितीय नियम(Kepler’s Second Law):सूर्य से ग्रह तक खींची हुई ध्रुवान्तर रेखाओं की गति से कक्षा समतल में रचित क्षेत्रफल समान समयों में समान होता है।
(The areas described by the radii drawn from the planet to the sun in the same orbit,proportional to the times of describing them.)
(3.)केप्लर का तृतीय नियम(Kepler’s Third Law):विभिन्न ग्रहों के परिक्रमण काल का वर्ग उनकी कक्षाओं के दीर्घाक्षों के घन के समानुपाती होता।
(The Squares of the periodic times of the planets are proportional to the cubes of the semi major axis of their orbits.)
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Central Orbit Dynamics
2.ग्रहों की गति के लिए केप्लर के नियम के उदाहरण (Laws of Kepler for Planetary Motion Examples):
Example:1.एक दिए हुए दीर्घवृत्त (जिसका दीर्घाक्ष 2a है) में यदि किसी विशेष बिन्दु P पर वेग समान है, चाहे कक्षा की रचना एक नाभि के परित: परिक्रमण काल T हो या दूसरी नाभि S’ के परित: परिक्रमण काल T’ हो, सिद्ध करो कि
SP=\frac{\left(2 a T^{\prime}\right)}{\left(T+T^{\prime}\right)}, S^{\prime} P=\frac{(2 a T)}{\left(T+ T^{\prime}\right)}
(If the velocity in a given orbit (major axis 2a) is same at a certain point P whether the orbit is being described in periodic time T about one focus S or in periodic time T’ about the other focus S’, prove that
SP=\frac{\left(2 a T^{\prime}\right)}{\left(T+T^{\prime}\right)}, S^{\prime} P=\frac{(2 a T)}{\left(T+ T^{\prime}\right)}
Solution:यदि SP=r तब S’P=2a-r
S को फोकस लिया जाए तथा S’ को रिक्त फोकस तब
v^{2}=\mu \left[\frac{2}{r}-\frac{1}{a}\right]
तथा T=\frac{2 \pi}{\sqrt{\mu}} a^{\frac{3}{2}} \cdots (1)
पुनः S’ को फोकस तथा S’ को रिक्त फोकस लें तब
S’P=2a-r रखने पर
V^{2}=\mu^{\prime}\left[\frac{2}{2 a-r}-\frac{1}{a}\right]
तथा T^{\prime}=\frac{2 \pi}{\sqrt{\mu^{\prime}}} a^{\frac{3}{2}} \ldots(2)
वेग समान दिया हुआ है अर्थात् v^{2}=V^{2}
\mu\left[\frac{2}{r}-\frac{1}{a}\right]=\mu^{\prime}\left[\frac{2}{2 a-r}-\frac{1}{a}\right] \cdots(3)
अब \mu=\frac{4 \pi^{2}}{T^{2}} तथा \mu^{\prime}=\frac{4 \pi^{2}}{T^{\prime^{2}}} a^{3}
\mu तथा \mu^{\prime} का मान समीकरण (3) में रखने पर:
\frac{4 \mu^{2}}{T^{2}} a^{3}\left[\frac{2}{r}-\frac{1}{a}\right]=\frac{4 \pi^{2}}{T^{\prime^{2}}} a^{3}\left[\frac{2}{2 a-r}-\frac{1}{a}\right] \\ \Rightarrow \frac{1}{T^{2}} \cdot \frac{2 a-r}{a r}=\frac{1}{T^{\prime^{2}}} \cdot \frac{r}{a(2 a-r)} \\ \Rightarrow T^{\prime 2}\left(2 a-r\right)^{2}=T^{2} r^{2} \\ \Rightarrow T^{\prime^{2}}\left(2 a-r\right)^{2}=T^{2} r^{2} \\ \Rightarrow T^{\prime}(2 a-r)=T \cdot r \\ \Rightarrow 2 a \cdot T^{\prime}=r \left(T+T^{\prime}\right) \\ \Rightarrow S P=r=\frac{2 a T^{\prime}}{T+T^{\prime}} \\ \Rightarrow S^{\prime} P=2 a-r=2 a-\frac{2 a T^{\prime}}{T+T^{\prime}} \\ \Rightarrow S^{\prime} P=\frac{2 a T}{(T+T^{\prime})}
उपर्युक्त प्रश्न के उत्तर द्वारा ग्रहों की गति के लिए केप्लर के नियम (Laws of Kepler for Planetary Motion),ग्रहों की गति के लिए केप्लर के नियम हिन्दी में (Laws of Kepler for Planetary Motion in hindi) के बारे में ओर अधिक जानकारी प्राप्त कर सकते है।
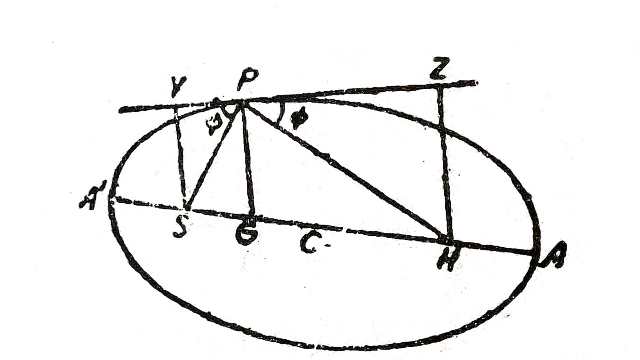
Example:2.एक कण नाभि में स्थित बल केन्द्र के प्रति एक दीर्घवृत्त बनाता है।प्रदर्शित कीजिए कि इसके पथ के किसी भी बिन्दु पर दूसरी नाभि के सापेक्ष कोणीय वेग उस बिन्दु पर अभिलम्ब के वर्ग के व्युत्क्रमानुपाती होती है।
(A particle describes about a centre of force at the focus.Show that at any point of its path the angular velocity about the other focus varies inversely as the square of the normal at that point.)
Solution:सकेन्द्र कक्षा के लिए
vp=h=r^{2} \frac{d \theta}{d t}=SP^{2} \cdot \frac{d \theta}{d t}
जहाँ \frac{d \theta}{d t} फोकस S के सापेक्ष कोमीय वेग है।यदि फोकस H के सापेक्ष कोणीय वेग \omega है तो
vp=a=HP^{2} \omega \\ \Rightarrow v HZ=H P^{2} \cdot \omega \\ \Rightarrow v=\frac{h}{p}=\frac{h}{S Y} \\ \Rightarrow \frac{h}{SY} HZ=HP^{2} \omega \\ \Rightarrow w=\frac{h}{S Y} \cdot \frac{H Z}{H P^{2}} \\ \Rightarrow w=\frac{h}{SY \cdot H P} \cdot \frac{H Z}{H P} \cdots(1)
अब \triangle SPY तथा \triangle HPZ में
\angle S P Y=\angle H P Z=\phi \\ \angle S Y P=\angle H Z P=\frac{\pi}{2}
कोण-कोण समरूपता गुणधर्म से (By AA Congruence Property)
\triangle S P Y \sim \triangle H P Z \\ \frac{H Z}{H P}=\frac{S Y}{S P} \cdots(2)
समीकरण (1) व (2) से:
\omega =\frac{h}{S Y \cdot H P} \cdot \frac{S Y}{SP} \\ =\frac{h}{SP \cdot H P} \\ =\frac{h}{(a+e x) \cdot (a-e x)} \\ \omega =\frac{h}{a^{2}-e^{2} x^{2}} \\ =\frac{h}{a^{2}-e^{2} a^{2} \cos ^{2} t}
[यदि बिन्दु ( a \cos t, b \sin t ) लिया जाए]
\Rightarrow w=\frac{h}{a^{2}-\left(a^{2}-b^{2}\right) \cos^{2} t} \\ w=\frac{h}{a^{2} \sin^{2} t+b^{2} \cos ^{2} t} \cdots(3)
बिन्दु P पर अभिलम्ब की समीकरण:
\frac{a x}{\cos t}-\frac{b y}{\sin t}=a^{2}-b^{2}
यह दीर्घाक्ष को G बिन्दु पर y=0 पर मिलता है जिसके निर्देशांक हैं
\left(\frac{a^{2}-b^{2}}{a} \cos t, 0\right) तथा (a \cos t, b \sin t)
अभिलम्ब की लम्बाई का वर्ग
=P G^{2}=\left(a \cos t-\frac{a^{2}-b^{2}}{a} \cos t\right)^{2}+b^{2} \sin ^{2} t \\ =\frac{b^{4}}{a^{2}} \cos ^{2} t+b^{2} \sin ^{2} t \\ \Rightarrow P G^{2}=\frac{b^{2}}{a^{2}}\left(b^{2} \cos ^{2} t+a^{2} \sin^{2} t \right) \cdots (4) \\ PG^{2}=\frac{b^{2}}{a^{2}} \cdot \frac{h}{\omega} [समीकरण (3) व (4) से ]
w=\frac{b^{2}}{a^{2}} \cdot h \cdot \frac{1}{PG^{2}} \\ \omega \propto \frac{1}{PG^{2}}
उपर्युक्त प्रश्न के उत्तर द्वारा ग्रहों की गति के लिए केप्लर के नियम (Laws of Kepler for Planetary Motion),ग्रहों की गति के लिए केप्लर के नियम हिन्दी में (Laws of Kepler for Planetary Motion in hindi) के बारे में ओर अधिक जानकारी प्राप्त कर सकते है।
Example:3.यदि दीर्घाक्ष के निकटतम सिरे पर कोणीय वेग w है, तब सिद्ध कीजिए कि इसका परिक्रमण काल \frac{2 \pi}{\omega} \sqrt{\frac{1+e}{(1-e)^{3}}} होगा।
(If w be the angular velocity at the near end of the major axis, prove that its period is.)
\frac{2 \pi}{\omega} \sqrt{\frac{1+e}{(1-e)^{3}}}
Solution:A’ के निकटतम सिरे पर
r=SA'=a-ae=a(1-e) \\ r^{2} \frac{d \theta}{d t}=h=\sqrt{(\mu l)} \quad[\because h=\sqrt{\mu l}]\\ \Rightarrow a^{2}(1-e)^{2} \omega=\sqrt{\left(\mu \cdot \frac{b^{2}}{a}\right)}\\ =\sqrt{\left[\mu a\left(1-e^{2}\right)\right]}\\ \Rightarrow \sqrt{\mu}=\frac{a^{2}(1-e)^{2} \omega}{\sqrt{[a(1-e)(1+e)}} \\ \Rightarrow \sqrt{\mu}=\frac{a^{\frac{3}{2}}(1-e)^{\frac{3}{2}}}{\sqrt{(1+e)}} \omega
यदि T आवर्तकाल हो तो
T =\frac{2 \pi}{\sqrt{\mu}} a^{\frac{3}{2}} \\ \Rightarrow T =\frac{2 \pi}{\omega} \sqrt{\frac{1+e}{(1-e)^{3}}} [समीकरण (1) से]
उपर्युक्त प्रश्न के उत्तर द्वारा ग्रहों की गति के लिए केप्लर के नियम (Laws of Kepler for Planetary Motion),ग्रहों की गति के लिए केप्लर के नियम हिन्दी में (Laws of Kepler for Planetary Motion in hindi) के बारे में ओर अधिक जानकारी प्राप्त कर सकते है।
Example:4.किसी ग्रह का सूर्य के चारों ओर सकेन्द्र कक्षा में अधिकतम एवं न्यूनतम वेग क्रमशः 30 तथा 29.2 km/sec है।सकेन्द्र कक्षा की उत्केन्द्रता ज्ञात कीजिए।
(The greatest and least velocities of a certain planet in its orbit round the sun are 30 and 29.2 km/sec.Find the eccentricity of the orbit.)
Solution:माना कि सूर्य दीर्घवृत्त की नाभि S में स्थित है तथा ग्रह की सबसे पास स्थिति A’ पर है जहाँ
SA’=A’C-SC=a(1-e)
तथा ग्रह की सबसे दूर स्थिति A पर है जहाँ
SA=SC+CA=a(1+e)
पुनः ग्रह का पथ दीर्घवृत्त है,
v^{2}=\mu \left(\frac{2}{r}-\frac{1}{a}\right) \\ \Rightarrow v_{1}^{2}=\mu\left[\frac{2}{a(1-e)}-\frac{1}{a}\right] \\ \Rightarrow 30^{2}=\frac{\mu}{a}\left(\frac{1+e}{1-e}\right) \quad\left[\because v_{1}=30\right] \\ \Rightarrow 900=\frac{\mu}{a}\left(\frac{1+e}{1-e}\right) \cdots(1) \\ v_{2}^{2}=\mu\left[\frac{2}{a(1+e)}-\frac{1}{a}\right] \\ (29.2)^{2}=\frac{\mu}{a}\left[\frac{1-e}{1+e}\right] \\ \Rightarrow 852.64=\frac{\mu}{9}\left(\frac{1-e}{1+e}\right) \cdots(2)
समीकरण (1) में (2) का भाग देने पर:
\frac{900}{852-64}=\frac{(1+e)^{2}}{(1-e)^{2}} \\ \Rightarrow \frac{30}{29.2}=\frac{1+e}{1-e} \\ \Rightarrow 30-30 e=29 \cdot 2+29 \cdot 2 e \\ \Rightarrow 29.2 e+30 e=30-29.2 \\ \Rightarrow 59.2 e=0.8 \\ \Rightarrow e=\frac{0.8}{59.2} \\ \Rightarrow e=\frac{1}{74}
उपर्युक्त उदाहरणों के द्वारा ग्रहों की गति के लिए केप्लर के नियम (Laws of Kepler for Planetary Motion) को समझ सकते हैं।
3.ग्रहों की गति के लिए केप्लर के नियम की समस्याएं (Laws of Kepler for Planetary Motion Problems):
(1.)एक कण दीर्घवृत्त में नाभि S की ओर केन्द्रित किसी बल के अधीन चलता है।जब कण लघुअक्ष के एक सिरे पर होता है तो गति की दिशा को बिना बदलते हुए इसकी गतिज ऊर्जा को दो गुना कर दिया जाता है।सिद्ध कीजिए कि ऐसा करने से कण एक परवलय में चलने लगेगा।
(A particle describes an ellipse under a force to the focus S.When the paricle is at one extremity of the minor axis, its kinetic energy is doubled without any change in the direction of motion.Prove that the paricle proceeds to describe a parabola.)
(2.)यदि तथा किसी ग्रह के रेखीय वेग हों जबकि वह सूर्य से क्रमशः न्यूनतम और अधिकतम दूरियों पर है तो सिद्ध कीजिए कि (1-e) v_{1}=(1+e) v_{2}
(If and are the velocities of a planet when it is respectively nearest farthest from the sun, prove that (1-e) v_{1}=(1+e) v_{2} )
(3.)एक कण नाभिका में स्थित बल केंद्र के प्रति एक दीर्घवृत्त निर्मित करता है जिसकी उत्केन्द्रता e है तो सुस्थापित (सामान्य संकेतों) में सिद्ध कीजिए:
v^{2}=\mu\left(\frac{2}{r}-\frac{1}{a}\right), h^{2}=\mu a \left(1-e^{2}\right)
जब कण निकटतम स्तब्धिका पर आता है तब केन्द्र दूसरे नाभि पर स्थानान्तरण कर दिया जाता है।सिद्ध कीजिए कि नये सकेन्द्र कक्षा की उत्केन्द्रता [\frac{e(3+e)}{(1-e)}]
(A particle is describing an ellipse of eccentricity e about a centre force at a focus , prove with the usual notations:
v^{2}=\mu\left(\frac{2}{r}-\frac{1}{a}\right), h^{2}=\mu a\left(1-e^{2}\right)
When the paricle is at the nearer apse, the centre of force is transferred to the other focus.Prove that the eccentricity of the new orbit is [\frac{e(3+e)}{(1-e)}])
उपर्युक्त प्रश्नों को हल करने पर ग्रहों की गति के लिए केप्लर के नियम (Laws of Kepler for Planetary Motion) को ठीक से समझ सकते हैं।
Also Read This Article:-Kepler Laws for Planetary Motion
4.ग्रहों की गति के लिए केप्लर के नियम (Laws of Kepler for Planetary Motion) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.केप्लर के ग्रह गति के 3 नियम क्या हैं? (What are Kepler’s 3 laws of planetary motion?):
उत्तर:वास्तव में तीन हैं,केप्लर के नियम जो ग्रहों की गति के हैं:(1.)प्रत्येक ग्रह की कक्षा एक दीर्घवृत्त है जिसमें सूर्य एक फोकस पर है;(2.) सूर्य और ग्रह को मिलाने वाली रेखा समान समय में समान क्षेत्रफलों को पार करती है;और (3.) किसी ग्रह की कक्षीय अवधि का वर्ग उसके अर्ध-दीर्घाक्ष अक्ष के घन के समानुपाती होता है।
प्रश्न:2.केप्लर ने ग्रहों को परिभाषित करने के लिए कितने नियमों का प्रयोग किया? (How many laws did Kepler use to define planetary?):
उत्तर:तीन नियम
उस प्रक्रिया का अन्वेषण करें जो जोहान्स केप्लर (Johannes Kepler) ने ग्रहों की गति के अपने तीन नियमों को तैयार करते समय की थी।
प्रश्न:3.ग्रहों की गति के केप्लर के नियम से इसे क्या व्युत्पन्न किया गया है? (What are Kepler’s law of planetary motion derive it?):
उत्तर:केप्लर के नियम केंद्रीय व्युत्क्रम वर्ग बल (central inverse square force) की उपस्थिति में वस्तुओं की गति का वर्णन करते हैं।किसी ग्रह की कक्षीय परिक्रमण अवधि का वर्ग उसकी कक्षा के अर्ध-दीर्घाक्ष के घन के समानुपाती होता है,अर्थात्
T^2 \propto r^3।
प्रश्न:4.केप्लर के तीसरे नियम में G क्या है? (What is G in Kepler’s third law?):
उत्तर;न्यूटोनियन स्थिरांक,G को दो द्रव्यमानों के बीच कुछ निश्चित दूरी द्वारा अलग किए गए बल के रूप में परिभाषित किया गया है।k को मापने के लिए,आपको केवल दिनों की गणना करने की आवश्यकता है;G को मापने के लिए,आपको प्रयोगशाला में परीक्षण वस्तुओं के बीच के द्रव्यमान,पृथक्करण (separation) और बलों को बहुत सटीक रूप से जानना होगा।
प्रश्न:5.क्या केप्लर के नियम सत्य हैं? (Are Kepler’s laws True?):
उत्तर:ग्रहों की गति की भविष्यवाणी करने के लिए केप्लर के नियम उपयोगी होते हैं।किसी ग्रह का अवलोकन उसकी केप्लरियन कक्षा निर्धारित कर सकता है और उससे हम उसके भविष्य के पथ की गणना कर सकते हैं।यह कि नियम असत्य हैं,केवल यह दर्शाता है कि भविष्यवाणियां सही नहीं होंगी।
प्रश्न:6.केप्लर के नियम क्या साबित नहीं करते थे? (What did Kepler’s laws not prove?):
उत्तर:केप्लर के नियम ग्रहों की गति के वर्णन (description) के रूप में अद्भुत हैं।हालांकि,वे इस बात का कोई स्पष्टीकरण नहीं देते हैं कि ग्रह इस तरह से क्यों चलते हैं।इसके अलावा, केप्लर का तीसरा नियम केवल सूर्य के चारों ओर ग्रहों के लिए काम करता है और पृथ्वी के चारों ओर चंद्रमा की कक्षा या बृहस्पति (Jupiter) के चंद्रमाओं पर लागू नहीं होता है।
प्रश्न:7.किसी ग्रह की कक्षा में सूर्य के निकटतम बिंदु को क्या कहते हैं? (What is the closest point to the sun in a planets orbit called?):
उत्तर:सूर्य उपसौर (perihelion)
ग्रहों के लिए,उनकी कक्षा में सूर्य के सबसे निकट का बिंदु पेरिहेलियन (perihelion) है।सबसे दूर के बिंदु को अपसौर,एपेलियन (aphelion) कहा जाता है।
प्रश्न:8.सूरज क्यों डगमगाता है? (Why does the sun wobble?):
उत्तर:सूर्य,पृथ्वी और सौर मंडल के सभी ग्रह इस बायरसेंटर (barycenter) के चारों ओर परिक्रमा करते हैं।यह संयुक्त रूप से सौर मंडल में प्रत्येक वस्तु के द्रव्यमान का केंद्र है।हमारे सौर मंडल का बैरीसेंटर (barycenter) लगातार स्थिति बदलता रहता है।जैसे ही सूर्य इस गतिमान बेरीसेंटर (barycenter) की परिक्रमा करता है,यह चारों ओर घूमता (wobbles) है।
प्रश्न:9.1609 में ग्रहों की गति के नियम की खोज किसने की थी? (Who discovered the law of planetary motion in 1609?):
उत्तर:टाइको (Tycho) द्वारा एकत्र किए गए सटीक डेटा का उपयोग करते हुए,केप्लर ने पाया कि मंगल (Mars) की कक्षा एक दीर्घवृत्त है।1609 में उन्होंने एस्ट्रोनोमिया नोवा (Astronomia Nova) को प्रकाशित किया,जिसमें उनकी खोजों को चित्रित किया गया था,जिन्हें अब केप्लर के ग्रहों की गति के पहले दो नियम कहा जाता है।
प्रश्न:10.ब्राहे का सबसे प्रसिद्ध छात्र कौन था? (Who was Brahe’s most famous student?):
उत्तर:ब्राहे का सबसे प्रसिद्ध छात्र
ब्राहे एक कुलीन व्यक्ति थे और केप्लर एक ऐसे परिवार से थे जिसके पास खाने के लिए मुश्किल से ही पर्याप्त पैसा था।
प्रश्न:11.क्या केप्लर ने ब्राहे से चोरी की थी? (Did Kepler steal from Brahe?):
उत्तर:वैज्ञानिकों ने 16वीं सदी के डेनिश खगोलशास्त्री टाइको ब्राहे (Danish astronomer Tycho Brahe) के शव को अभी-अभी निकाला है।हालांकि केप्लर ने डेटा चुरा लिया था जो ब्राहे के उत्तराधिकारियों को विरासत में मिला था और खगोलशास्त्री (astronomer) की मृत्यु के बाद देश से भाग गया था।
प्रश्न:12.पृथ्वी की उत्केन्द्रता क्या है? (What is Earth eccentricity?):
उत्तर:पृथ्वी की कक्षीय उत्केन्द्रता e एक वृत्त के आकार से पृथ्वी के कक्षीय पथ के विचलन को मापती है।पृथ्वी की वर्तमान उत्केन्द्रता e≈0.01671 है।अतीत में यह 0 और ∼0.06 के बीच भिन्न (varied) था।
प्रश्न:13.ग्रह किस बिंदु पर सबसे तेज गति व सबसे धीमी गति से चलता है? (At which point does the planet move the fastest the slowest?):
उत्तर:एक ग्रह लगातार बदलती गति के साथ चलता है क्योंकि यह अपनी कक्षा में घूमता है।सबसे तेज गति से चलने वाला ग्रह पेरीहेलियन (निकटतम,closest) [perihelion] पर होता है और सबसे धीमा एपेलियन (सबसे दूर,farthest) [aphelion] पर होता है।
प्रश्न:14.सूरज कितनी दूर डगमगाता है? (How far does the sun wobble?):
उत्तर:पृथ्वी का सूर्य पर खिंचाव इसे इससे 330,000 गुना कम ले जाता है।यानी करीब 560 मील।तुलना में ज्यादा नहीं।तो आप दूर से ही देखते हैं कि सूर्य वर्ष में लगभग 560 मील आगे-पीछे घूमता है,लेकिन एक चतुर एलियन (clever alien) के लिए यह जानने के लिए पर्याप्त है कि पृथ्वी है।
प्रश्न:15.पृथ्वी के डगमगाने को क्या कहते हैं? (What is the wobble of the Earth called?):
उत्तर:पुरस्सरण (precession)
मिलनकोविच (Milankovich) ने जिस तीसरे कक्षीय परिवर्तन का अध्ययन किया,उसे पुरस्सरण (precession) कहा जाता है,एक चक्र में पृथ्वी की धुरी का चक्रीय कंपन (Cyclical Wooble)।गति एक घूर्णन शीर्ष (spinning top) की तरह होती है जब वह गिरने वाली होती है।पृथ्वी के एक पूर्ण चक्र में लगभग 26,000 वर्ष लगते हैं।
प्रश्न:16.तारे कितना डगमगाते हैं? (How much do stars wobble?)
उत्तर:रॉय का कहना है कि यह उपकरण वर्तमान में लगभग 30 सेंटीमीटर प्रति सेकंड की तारकीय गति का पता लगा सकता है,लेकिन उनका अंतिम लक्ष्य कुछ सितारों पर 10 सेंटीमीटर प्रति सेकंड तक नीचे जाने का प्रयास करना है – जिस गति से हमारा सूर्य पृथ्वी के टग (पृथ्वी के खिंचाव) (Earth’s Tug) के कारण चलता है।
प्रश्न:17.टाइको ने अपनी नाक कैसे खो दी? (How did Tycho lose his nose?):
उत्तर:टाइको ब्राहे (1546-1601) एक डेनिश खगोलशास्त्री (Danish astronomer) थे।जब वह 20 साल के थे,तब ब्राहे ने अपने तीसरे चचेरे भाई,मंडेरुप पार्सबर्ग (Manderup Parsberg) के साथ तलवार के द्वंद्व में अपनी नाक का हिस्सा खो दिया।मंडेरुप के ब्लेड ने नाक के अधिकांश पुल को काट दिया,जिससे नाक गुहा और सेप्टम उजागर हो गया।
प्रश्न:18.टाइको ब्राहे ने क्या साबित किया? (What did Tycho Brahe prove?):
उत्तर:टाइको ब्राहे ने तारों और ग्रहों का सटीक अवलोकन किया।1572 में प्रकट हुए “नए तारे” के उनके अध्ययन से पता चला कि यह चंद्रमा से अधिक दूर था और स्थिर तारों में से था,जिन्हें पूर्ण और अपरिवर्तनीय माना जाता था।
प्रश्न:19.टाइको ब्राहे को किसने मारा? (What killed Tycho Brahe?):
उत्तर:24 अक्टूबर 1601
टाइको ब्राहे (Tycho Brahe)/मृत्यु तिथि
प्रश्न:20.टाइको ब्राहे का खगोल विज्ञान में सबसे बड़ा योगदान क्या था? (What was the greatest contribution of Tycho Brahe to astronomy?):
उत्तर:उन्होंने व्यापक खगोलीय अवलोकन करने के लिए सबसे पहले दूरबीन का उपयोग किया।उन्होंने निर्धारित किया कि ग्रह अण्डाकार (दीर्घवृत्तीय) कक्षाओं में सूर्य की परिक्रमा करते हैं।उन्होंने कुछ सरल नियमों का प्रस्ताव रखा जो ग्रहों और अन्य वस्तुओं की गति को नियंत्रित करते हैं।
प्रश्न:21.क्या उत्केन्द्रता जलवायु को प्रभावित करती है? (Does eccentricity affect climate?):
उत्तर:उत्केंद्रता मापती है कि पृथ्वी की कक्षा का आकार एक पूर्ण वृत्त से कितना अलग है।ये विचलन (variations) पृथ्वी और सूर्य के बीच की दूरी को प्रभावित करती हैं।क्योंकि पृथ्वी की उत्केन्द्रता में विचलन काफी कम हैं,वे वार्षिक मौसमी जलवायु विविधताओं में एक अपेक्षाकृत मामूली कारक हैं।
प्रश्न:22.उत्केन्द्रता का सूत्र क्या है? (What is eccentricity formula?):
उत्तर:उत्केन्द्रता सूत्र
किसी भी शंकु खंड की उत्केन्द्रता ज्ञात करने के सूत्र को इस प्रकार परिभाषित किया गया है:उत्केन्द्रता, e = c/a।जहाँ c=केंद्र से फोकस की दूरी।a=केंद्र से शीर्ष तक की दूरी।
प्रश्न:23.क्या सूर्य पृथ्वी की कक्षा के केंद्र में है? (Is the sun in the center of Earth orbit?):
उत्तर:सूर्य पृथ्वी की कक्षा के केंद्र में नहीं है।
प्रश्न:24.टाइको ब्राहे की नाक कैसी दिखती थी? (What did Tycho Brahe’s nose look like?):
उत्तर:अलग-अलग, परीक्षणों से पता चला कि ब्राहे की प्रसिद्ध “सिल्वर” कृत्रिम नाक वास्तव में पीतल से बनी थी। 1546 में डेनमार्क में जन्मे,ब्राहे ने पवित्र रोमन सम्राट रूडोल्फ II के दरबार में प्राग (Prague in the court of Holy Roman Emperor Rudolph II) में बसने से पहले डेनिश राजा के लिए एक खगोलशास्त्री के रूप में कार्य किया।
प्रश्न:25.क्या केप्लर ने अपनी नाक खो दी? (Did Kepler lose his nose?):
उत्तर:1901 में हेनरिक मटिग्का (Heinrich Matiegka) के नेतृत्व में एक टीम ने प्राग में ब्राहे की कब्र खोली,यह पता लगाने की उम्मीद में कि क्या उनके अवशेष अभी भी वहां थे।जबकि ब्राहे अभी भी अपने ताबूत में थे,उनकी प्रसिद्ध नाक नहीं थी। निराशाजनक रूप से, ऐसा प्रतीत हुआ कि उसे या तो इसके बिना दफनाया गया था या वह एक के साथ जो आसानी से विघटित हो गया था।
प्रश्न:26.टाइको का प्रमुख योगदान क्या है? (What is the major contribution of Tycho?):
उत्तर:एक डेनिश रईस,टाइको ब्राहे (1546-1601) ने आकाश को देखने के लिए दूरबीन के आविष्कार से पहले उपलब्ध सबसे सटीक उपकरणों को तैयार करके महत्वपूर्ण योगदान दिया।ब्राहे ने डेनमार्क और स्वीडन के बीच हवेन (Hveen) नामक एक द्वीप पर यूरानिबोर्ग (Uraniborg) से अपने अवलोकन किए।
प्रश्न:27.टाइको ब्राहे की विरासत क्या थी? (What was Tycho Brahe legacy?):
उत्तर:ब्राहे द्वारा खोजे गए सुपरनोवा को आज एसएन 1572 कहा जाता है।इसके अलावा,टाइको ब्राहे ने धूमकेतु की एक बार इतनी रहस्यमय घटना को समझाने के लिए एक आवश्यक शर्त बनाई।उन्होंने पाया कि ये खगोलीय पिंड हैं जो पृथ्वी से शनि ग्रह (Saturn) से कहीं अधिक दूर हो सकते हैं।
प्रश्न:28.ब्राहे को जहर किसने दिया? (Who poisoned Brahe?):
उत्तर:जोहान्स केप्लर
एक हत्या सिद्धांत कहता है कि ब्राहे को डेनिश राजा क्रिश्चियन IV के आदेश पर मार दिया गया था,जिसके साथ वह गिर गया था या उसके अब और अधिक प्रसिद्ध सहायक जोहान्स केप्लर ने ब्राहे के खगोलीय अवलोकनों पर अपना हाथ पाने के लिए उसकी हत्या कर दी थी।
प्रश्न:29.क्या टाइको ब्राहे का मूत्राशय फट गया था? (Did Tycho Brahe’s bladder burst?):
उत्तर:लंबे समय से माना जाता था कि ब्राहे की मूत्राशय के संक्रमण से मृत्यु हो गई थी,क्योंकि विनम्रता ने उन्हें अक्टूबर 1601 में एक शाही भोज के दौरान बाथरूम का उपयोग करने के लिए खुद को बहाने से रोक दिया,जिससे उनका मूत्राशय फट गया।
प्रश्न:30.क्या उत्केन्द्रता नकारात्मक हो सकता है? (Can eccentricity be negative?):
उत्तर:उत्केंद्रता एक ट्रैवर्सिंग बिंदु के लिए दो लंबाई (अधिक सटीक दूरी) का अनुपात है,एक विशेष बिंदु से मापा जाता है और दूसरा एक विशेष रेखा से होता है।आप कभी भी नकारात्मक उत्केन्द्रता नहीं प्राप्त कर सकते क्योंकि लंबाई हमेशा धनात्मक होती है।
प्रश्न:31.एक सीधी रेखा की उत्केन्द्रता क्या है? (What is the eccentricity of a straight line?):
उत्तर:तो एक अतिपरवलय जिसकी अनुप्रस्थ अक्ष और संयुग्मी अक्ष की लंबाई शून्य हो जाती है,सीधी रेखाओं का एक युग्म बन जाता है।अतः सीधी रेखाओं के एक युग्म की उत्केन्द्रता >1 होगी।
प्रश्न:32.एक दीर्घवृत्त की न्यूनतम उत्केन्द्रता क्या हो सकती है? (Why does elliptical eccentricity have no unit?):
उत्तर:शून्य
उत्तर:इसलिए,एक दीर्घवृत्त की उत्केन्द्रता का न्यूनतम मान शून्य है और यह तब होता है जब दीर्घवृत्त एक वृत्त के साथ मेल खाता है।
प्रश्न:33.क्या उत्केन्द्रता हमेशा 1 से कम होती है? (Is eccentricity always less than 1?):
उत्तर:शंकु खंड (conic section)
एक अचर है,जिसे वक्र की उत्केन्द्रता कहते हैं।यदि उत्केंद्रता शून्य है,तो वक्र एक वृत्त है;यदि एक के बराबर, एक परवलय;यदि एक से कम, एक दीर्घवृत्त;और यदि एक से अधिक हो तो अतिपरवलय।
प्रश्न:34.अण्डाकार (दीर्घवृत्त) उत्केन्द्रता की कोई इकाई क्यों नहीं होती है? (Is eccentricity always less than 1?):
उत्तर:कक्षीय वेग (किमी/सेकेंड या मील/सेकेंड)-ग्रह की औसत गति या गति जब वह सूर्य की परिक्रमा करता है, किलोमीटर प्रति सेकंड या मील प्रति सेकंड में।जितना बड़ा उत्केंद्रता,उतनी ही लम्बी कक्षा,0 की उत्केन्द्रता का अर्थ है कि कक्षा एक पूर्ण वृत्त है।उत्केन्द्रता के लिए कोई इकाइयाँ नहीं हैं।
प्रश्न:35.किस आकृति की उत्केन्द्रता न्यूनतम है? (What figure has the minimum eccentricity?):
उत्तर:यह केवल एक वृत्त है।
प्रश्न:36.उत्केन्द्रता 0 और 1 के बीच क्यों होनी चाहिए? (Why must the eccentricity be between 0 and 1?):
उत्तर:एक दीर्घवृत्त के लिए उत्केन्द्रता 0 और 1 (0<e<1) के बीच होती है।जब उत्केंद्रता 0 होती है,तो नाभियाँ केंद्र बिंदु से संपाती होती हैं और आकृति एक वृत्त होती है। जैसे-जैसे उत्केन्द्रता 1 की ओर बढ़ती है,दीर्घवृत्त अधिक लम्बी आकृति प्राप्त करता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा ग्रहों की गति के लिए केप्लर के नियम (Laws of Kepler for Planetary Motion),ग्रहों की गति के लिए केप्लर के नियम हिन्दी में (Laws of Kepler for Planetary Motion in hindi) के बारे में ओर अधिक जानकारी प्राप्त कर सकते है।
उपर्युक्त प्रश्नों के उत्तर द्वारा ग्रहों की गति के लिए केप्लर के नियम (Laws of Kepler for Planetary Motion),ग्रहों की गति के लिए केप्लर के नियम हिन्दी में (Laws of Kepler for Planetary Motion in hindi) के बारे में ओर अधिक जानकारी प्राप्त कर सकते है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |