Green Theorem Proof
1.ग्रीन प्रमेय का प्रमाण (Green Theorem Proof,Proof of Green theorem)-
ग्रीन प्रमेय का प्रमाण (Green Theorem Proof,proof of Green theorem),का अध्ययन इस आर्टिकल में करेंगे। इससेे पूर्व आर्टिकल में गाॅस अपसरण प्रमेय तथा स्टोक्स प्रमेय के बारे में अध्ययन कर चुके हैं।
यदि आप गाॅस अपसरण प्रमेय तथा स्टोक्स प्रमेय के बारे में जानना चाहते हैं तो आपको उन आर्टिकल को पढ़ना चाहिए।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-How to solve stokes theorem?
(1.)ग्रीन की प्रमेय का कथन (Statement of Green Theorem)-
यदि \phi तथा \psi दो सतत अवकलनीय बिन्दु फलन इस प्रकार हैं कि \nabla \phi तथा \nabla \psi सतत,अवकल्य क्षेत्र V में जो कि पृष्ठ S से घिरा हुआ है,तो
(Statement of Green Theorem: If \phi and \psi are scalar point functions which together with their directives in any direction, \nabla \phi and \nabla \psi are uniform and continuous within the region V bounded by a closed surface S,then)
{ \int }_{ v }(\phi { \nabla }^{ 2 }\psi -\psi { \nabla }^{ 2 }\phi )dv={ \int }_{ v }(\phi \nabla \psi -\psi \nabla \phi ).\hat { n } ds
Green Theorem Proof:
गाॅस डाइवर्जेन्स प्रमेय का प्रयोग सदिश \phi \nabla \psi पर करने पर
{ \int }_{ v }\phi \nabla \psi .\hat { n } ds={ \int }_{ v }div(\phi \nabla \psi )dv
परन्तु div(\phi \nabla \psi )=\nabla .(\phi \nabla \psi )\\ =\nabla \phi .\nabla \psi +\phi { \nabla }^{ 2 }\psi \quad \quad \quad ..........(2)
{ \int }_{ s }\phi \nabla \psi .\hat { n } ds={ \int }_{ \quad v }\nabla \psi .\nabla \phi dv+{ \int }_{ v }\phi { \nabla }^{ 2 }\psi dv\quad \quad \quad ....................(3)
(3) में का अन्त: परिवर्तन करने पर-
{ \int }_{ s }\psi \nabla \phi .\hat { n } ds={ \int }_{ \quad v }\nabla \phi .\nabla \psi dv+{ \int }_{ v }\psi { \nabla }^{ 2 }\phi dv ........(4)
(4) को (3) से घटाने पर-
{ \int }_{ s }(\phi \nabla \psi -\psi \nabla \phi ).\hat { n } ds={ { \int }_{ v } }(\phi { \nabla }^{ 2 }\psi -\psi { \nabla }^{ 2 }\phi dv)............(5)
जो कि ग्रीन प्रमेय को सिद्ध करता है।
(2.)ग्रीन प्रमेय का दूसरा रूप (Another form of Green Theorem)-
(5)का प्रथम सदस्य हम निम्न प्रकार लिख सकते हैं-
\int { (\phi \frac { \partial \psi }{ \partial n } -\psi \frac { \partial \phi }{ \partial n } ).ds } \frac { \partial \psi }{ \partial n }
क्षेत्र में सतह पर बाह्य की ओर अभिलम्ब की दिशा में का अवकलज है अर्थात्
\nabla \psi =\frac { \partial \psi }{ \partial n } \hat { n } ,\nabla \phi =\frac { \partial \phi }{ \partial n } \hat { n }
अतः ग्रीन प्रमेय का पुनः कथन है
{ { \int }_{ v } }(\phi { \nabla }^{ 2 }\psi -\psi { \nabla }^{ 2 }\phi dv)dv={ \int }_{ s }(\phi \frac { \partial \psi }{ \partial n } -\psi \frac { \partial \phi }{ \partial n } )\hat { n } ds
(3.)ग्रीन प्रमेय का कार्तीय रूप (Cartesian form of Green Theorem),ग्रीन प्रमेय सूत्र (green theorem formula)-
यदि C,XY तल में एक सतत् बन्द वक्र है जो कि क्षेत्र S को घेरता है तथा P(x,y) एवं Q(x,y) दो सतत् अवकलनीय फलन है तब
{ \iint }_{ s }(\frac { \partial \phi }{ \partial x } -\frac { \partial P }{ \partial y } )dxdy={ \int }_{ c }(Pdx+Qdy)
(If C is a regular closed curve,in xy-plane, enclosing a region S and P(x,y) and Q(x,y)be two continuously differentiable functions in the region S,i.e. inside and on C ,then
{ \iint }_{ s }(\frac { \partial \phi }{ \partial x } -\frac { \partial P }{ \partial y } )dxdy={ \int }_{ c }(Pdx+Qdy)
उपपत्ति (Proof)-माना F=P\hat { i } +Q\hat { j } और \because \hat { n } =\hat { k } तब
CurlF=\left| \begin{matrix} i & j & k \\ \frac { \partial }{ \partial x } & \frac { \partial }{ \partial y } & \frac { \partial }{ \partial z } \\ P & Q & O \end{matrix} \right| \\ \qquad =-i\frac { \partial \phi }{ \partial z } +j\frac { \partial P }{ \partial z } +k(\frac { \partial \phi }{ \partial x } -\frac { \partial P }{ \partial y } )\\ \therefore CurlF.n=CurlF.k=\frac { \partial \phi }{ \partial x } -\frac { \partial P }{ \partial y } \\ \Rightarrow { \int }_{ s }\nabla \times F.\hat { n } ds={ \int }_{ s }(\frac { \partial \phi }{ \partial x } -\frac { \partial P }{ \partial y } )dxdy.............(1)
तथा { \int }_{ c }F.dr=CurlF.k=\frac { \partial \phi }{ \partial x } -\frac { \partial P }{ \partial y } \\ \Rightarrow { \int }_{ s }\nabla \times F.\hat { n } ds={ \int }_{ s }(\frac { \partial \phi }{ \partial x } -\frac { \partial P }{ \partial y } )dxdy.............(1)
तथा { \int }_{ c }F.dr={ \int }_{ c }(Pi+Qj).(idx+jdy+kdz)\\ \qquad \qquad ={ \int }_{ c }(Pdx+Qdy)....(2)
(1) तथा (2) से (स्टाॅक प्रमेयानुसार)
{ \iint }_{ s }(\frac { \partial \phi }{ \partial x } -\frac { \partial P }{ \partial y } )dxdy={ \int }_{ c }(Pdx+Qdy)
2.ग्रीन प्रमेय का प्रमाण (Green Theorem Proof,Proof of Green theorem) पर आधारित उदाहरण,ग्रीन प्रमेय उदाहरण (Green Theorem Example)-
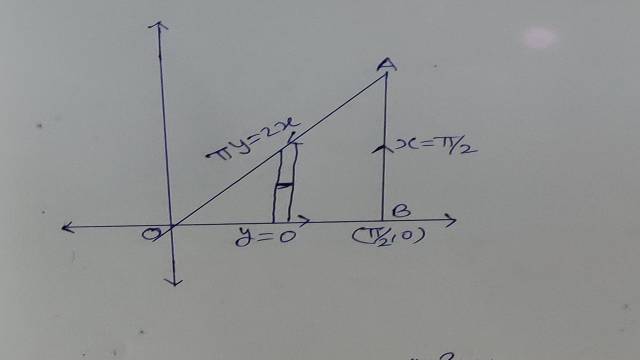
Question-1.समतल में ग्रीन प्रमेय के द्वारा { \int }_{ c }\{ (y-\sin { x } )dx+\cos { x } dy\} का मान ज्ञात कीजिए जबकि C ,y=0,x=\frac { \pi }{ 2 } ,\pi y=2x रेखाओं से बना (परिबन्ध) हुआ त्रिभुज है।
Solution–{ \int }_{ c }\{ (y-\sin { x } )dx+\cos { x } dy\} \\ P=y-\sin { x } \qquad \therefore \frac { \partial P }{ \partial y } =1
तथा Q=\cos { x } \qquad \therefore \frac { \partial \phi }{ \partial x } =-\sin { x } \\ \frac { \partial \phi }{ \partial x } -\frac { \partial P }{ \partial y } =-\sin { x } -1
रेखाओं y=0 ,x=\frac { \pi }{ 2 } तथा \pi y=2xके प्रतिच्छेदन बिन्दु (\frac { \pi }{ 2 } ,1) हैं। त्रिभुज पर धनात्मक दिशा में घूमने का पथ वह है जैसे चित्र में दर्शाया गया है।
अब ग्रीन प्रमेय से
{ \iint }_{ s }(\frac { \partial \phi }{ \partial x } -\frac { \partial P }{ \partial y } )dxdy=\int _{ x=0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ \frac { 2x }{ \pi } }{ (-\sin { x } -1)dxdy } } \\ =\int _{ x=0 }^{ \frac { \pi }{ 2 } }{ { [-y\sin { x } -y] }_{ 0 }^{ \frac { 2x }{ \pi } } } dx\\ =\int _{ x=0 }^{ \frac { \pi }{ 2 } }{ { [-\frac { 2x }{ \pi } \sin { x } -\frac { 2x }{ \pi } ] } } dx\\ ={ [\frac { 2x }{ \pi } \cos { x } ] }_{ 0 }^{ \frac { \pi }{ 2 } }-{ \frac { 2 }{ \pi } [\cos { x } ] }_{ 0 }^{ \frac { \pi }{ 2 } }-{ \frac { 1 }{ \pi } [{ x }^{ 2 }] }_{ 0 }^{ \frac { \pi }{ 2 } }\\ =0-\frac { 2 }{ \pi } -\frac { \pi }{ 4 } \\ =-(\frac { \pi }{ 4 } +\frac { 2 }{ \pi } )
सत्यापन (Verification): रेखा समाकलन C पर हम मान निकालते हैं-
रेखा OB पर,y=0,dy=0
\int _{ 0 }^{ \frac { \pi }{ 2 } }{ -sinxdx } =-1...(1)
रेखा BA पर,x=\frac { \pi }{ 2 } \therefore dx=0
\int _{ 0 }^{ 1 }{ dy } =0.........(2)
रेखा AO पर रेखा \pi y=2x समाकलन
\Rightarrow \pi dy=2dx\\ { \int }_{ c }\{ (y-\sin { x } )dx+\cos { x } dx\} \\ =\int _{ \frac { \pi }{ 2 } }^{ 0 }{ [(\frac { 2x }{ \pi } -\sin { x } )dx+(\cos { x } )(\frac { 2 }{ \pi } )dx] } \\ ={ [\frac { 1 }{ \pi } .{ x }^{ 2 }+\cos { x } +\frac { 2 }{ \pi } \sin { x } ] }_{ \frac { \pi }{ 2 } }^{ 0 }\\ =1-\frac { 1 }{ \pi } .\frac { { \pi }^{ 2 } }{ 4 } -0-\frac { 2 }{ \pi } \\ =1-\frac { { \pi } }{ 4 } -\frac { 2 }{ \pi } ....(3)
समीकरण (1),(2) तथा (3) को जोड़ने पर
=-(\frac { { \pi } }{ 4 } +\frac { 2 }{ \pi } )
अतः ग्रीन प्रमेय सत्यापित हुई।
Question-2.समाकलन { \int }_{ c }[(2{ x }^{ 2 }-{ y }^{ 2 })dx+({ x }^{ 2 }+{ y }^{ 2 })dy] का मान ज्ञात कीजिए जबकि C,xy-तल में x-अक्ष तथा अर्धवृत्त \\ y=\sqrt { 1-{ x }^{ 2 } } से घिरा हुआ पृष्ठ है।
Solution–{ \int }_{ c }[(2{ x }^{ 2 }-{ y }^{ 2 })dx+({ x }^{ 2 }+{ y }^{ 2 })dy]\\ P=2{ x }^{ 2 }-{ y }^{ 2 },\frac { \partial P }{ \partial y } =-2y\\ Q={ x }^{ 2 }+{ y }^{ 2 },\frac { \partial Q }{ \partial x } =2x\\ \frac { \partial Q }{ \partial x } -\frac { \partial P }{ \partial y } =2x+2y\\ =2(x+y)
रेखाओं x=-1,x=1,y=0 तथा \\ y=\sqrt { 1-{ x }^{ 2 } } वक्र के प्रतिच्छेदन के बिन्दु (-1,0),(1,0) है।
ग्रीन प्रमेय से-
\iint _{ S }^{ \quad }{ (\frac { \partial Q }{ \partial x } -\frac { \partial P }{ \partial y } )dxdy } =\int _{ -1 }^{ 1 }{ \int _{ 0 }^{ \sqrt { 1-{ x }^{ 2 } } }{ 2(x+y)dxdy } } \\ =\int _{ -1 }^{ 1 }{ { 2[xy+\frac { { y }^{ 2 } }{ 2 } ] }_{ 0 }^{ \sqrt { 1-{ x }^{ 2 } } }dx } \\ =\int _{ -1 }^{ 1 }{ { 2[x\sqrt { 1-{ x }^{ 2 } } +\frac { 1-{ x }^{ 2 } }{ 2 } ] }dx } \\ =2\int _{ -1 }^{ 1 }{ x\sqrt { 1-{ x }^{ 2 } } dx } +\int _{ -1 }^{ 1 }{ dx } -\int _{ -1 }^{ 1 }{ { x }^{ 2 }dx } \\ =-\frac { 2 }{ 3 } { [{ (1-{ x }^{ 2 }) }^{ \frac { 3 }{ 2 } }] }_{ -1 }^{ 1 }+{ [x] }_{ -1 }^{ 1 }-\frac { 1 }{ 3 } { [{ x }^{ 3 }] }_{ -1 }^{ 1 }\\ =-\frac { 2 }{ 3 } (0)+1+1-\frac { 1 }{ 3 } -\frac { 1 }{ 3 } \\ =2-\frac { 2 }{ 3 } \\ =\frac { 6-2 }{ 3 } \\ =\frac { 4 }{ 3 }
Question-3.प्रदर्शित कीजिए कि एक सरल रेखा बन्द वक्र C से घिरे हुए क्षेत्र का क्षेत्रफल\frac { 1 }{ 2 } \int { (xdy-ydx) } होता है। अतः दीर्घवृत्त x=a\cos { \theta } ,y=b\sin { \theta } का क्षेत्रफल ज्ञात कीजिए।
(Show that the area bounded a simple closed curve C is given by\frac { 1 }{ 2 } \int { (xdy-ydx) } .Hence find the area of the elipsex=a\cos { \theta } ,y=b\sin { \theta } )
Solution-हम जानते हैं कि { \iint }_{ s }(Mdx+Ndy)dxdy जहां S ,समतल क्षेत्र A है जो वक्र C से घिरा हुआ है।
M=-y तथा N=x
\frac { \partial M }{ \partial y } =-1 तथा \frac { \partial N }{ \partial x } =1\\ { \int }_{ c }(-ydx+xdy)={ \iint }_{ s }2dxdy\\ ={ 2\iint }_{ s }dxdy\\ =2A \\ A=\frac { 1 }{ 2 } \int { (xdy-ydx) }
दीर्घवृत्त की प्राचलिक समीकरण-
x=a\cos { \theta , } y=b\sin { \theta }
\theta का मान 0 से 2\pi तक बदलता है।
\therefore A=\frac { 1 }{ 2 } \int _{ 0 }^{ 2\pi }{ a\cos { \theta } (b\cos { \theta } d\theta )-(b\sin { \theta } )(-a\sin { \theta } d\theta ) } \\ =\frac { 1 }{ 2 } ab\int _{ 0 }^{ 2\pi }{ (\cos ^{ 2 }{ \theta } +\sin ^{ 2 }{ \theta } )d\theta } \\ =\frac { 1 }{ 2 } ab.2\pi \\ =\pi ab
Question-4.ग्रीन प्रमेय को तल में के लिए सत्यापित कीजिए,जहां C ,y={ x }^{ 2 } और x={ y }^{ 2 } से घिरे क्षेत्र की सीमा वक्र है)
(Verify Green theorem in the plane for,where C is the boundary of the region enclosed by y={ x }^{ 2 } andx={ y }^{ 2 })
Solution-y={ x }^{ 2 } और x={ y }^{ 2 } दोनों परवलय एक दूसरे को (0,0) तथा (1,1) पर प्रतिच्छेद करते हैं।
\int _{ c }^{ \quad }{ Mdx+Ndy } =\int _{ { c }_{ 1 } }^{ \quad }{ Mdx+Ndy } +\int _{ { c }_{ 2 } }^{ \quad }{ Mdx+Ndy }
{ c }_{ 1 } के लिए { x }^{ 2 }=y\\ dy=2xdx
तथा x की सीमा 0 से 1
{ c }_{ 1 } के लिए रेखा समाकलन
=\int _{ 0 }^{ 1 }{ \left( 2{ x }^{ 3 }-{ x }^{ 2 } \right) dx } +\left( { x }^{ 2 }+{ x }^{ 4 } \right) 2xdx\\ =\int _{ 0 }^{ 1 }{ (2{ x }^{ 3 }-{ x }^{ 2 }+2{ x }^{ 3 }+2{ x }^{ 5 })dx } \\ =\int _{ 0 }^{ 1 }{ (4{ x }^{ 3 }-{ x }^{ 2 }+2{ x }^{ 5 })dx } \\ ={ [{ x }^{ 4 }-\frac { { x }^{ 3 } }{ 3 } +\frac { { x }^{ 6 } }{ 3 } ] }_{ 0 }^{ 1 }\\ =1-\frac { 1 }{ 3 } -\frac { 1 }{ 3 } =1....(1)
{ c }_{ 2 } के लिए { y }^{ 2 }=x
2y dy=dx
y की सीमा 1 से 0 है।
{ c }_{ 2 } के लिए रेखा समाकलन
\int _{ 0 }^{ 1 }{ \left( 2{ y }^{ 3 }-{ y }^{ 4 } \right) 2ydy+\left( { y }^{ 4 }+{ y }^{ 2 } \right) dy } \\ =\int _{ 0 }^{ 1 }{ \left( 5{ y }^{ 4 }-2{ y }^{ 5 }+{ y }^{ 2 } \right) dy } \\ ={ [{ y }^{ 5 }-\frac { 1 }{ 3 } { y }^{ 6 }+\frac { 1 }{ 3 } { y }^{ 3 }] }_{ 1 }^{ 0 }\\ =-1+\frac { 1 }{ 3 } -\frac { 1 }{ 3 } \\ =-1...(2)
C के लिए रेखा समाकलन=1-1=0
पुनः
\int _{ c }^{ \quad }{ Mdx+Ndy } =\iint _{ S }^{ \quad }{ (\frac { \partial N }{ \partial x } -\frac { \partial M }{ \partial y } )dxdy } \\ M=2xy-{ x }^{ 2 },\frac { \partial M }{ \partial y } =2x\\ N={ x }^{ 2 }+{ y }^{ 2 },\frac { \partial N }{ \partial x } =2x\\ \frac { \partial N }{ \partial x } -\frac { \partial M }{ \partial y } =0...(3)\\ \iint _{ S }^{ \quad }{ (\frac { \partial N }{ \partial x } -\frac { \partial M }{ \partial y } )dxdy } =\iint _{ S }^{ \quad }{ 0dxdy } \\ =0
अतः ग्रीन प्रमेय सत्यापित हुई।
उपर्युक्त उदाहरणों के द्वारा ग्रीन प्रमेय का प्रमाण (Green Theorem Proof,Proof of Green Theorem) को समझा जा सकता है।
3.स्टोक्स प्रमेय कथन (stokes theorem statement)-
स्टोक का प्रमेय कथन है “एक बंद सतह से बंधी सतह पर एक फ़ंक्शन के कर्ल की सतह का समाकल भाग, उसके चारों ओर विशेष वेक्टर फ़ंक्शन के लाइन इंटीग्रल के बराबर होगा।” स्टोक्स प्रमेय लाइन इंटीग्रल्स और सतह इंटीग्रल्स के बीच एक संबंध देता है।
4.ग्रीन प्रमेय के अनुप्रयोग (Green theorem application)-
ग्रीन की प्रमेय में यह कथन कि दो अलग-अलग प्रकार के समाकल समान हैं, दोनों प्रकार की गणना करने के लिए उपयोग किया जा सकता है: कभी-कभी ग्रीन के प्रमेय का उपयोग एक लाइन इंटीग्रल को एक डबल इंटीग्रल में बदलने के लिए किया जाता है, और कभी-कभी इसका उपयोग एक डबल इंटीग्रल को एक लाइन इंटीग्रल में बदलने के लिए किया जाता है।
5.इलेक्ट्रिकल इंजीनियरिंग में ग्रीन प्रमेय के अनुप्रयोग (Green theorem applications in electrical engineering)-
एक क्षेत्र R को घेरते हुए G में एक बंद वक्र C को देखते हुए, आर। ग्रीन का प्रमेय आश्वासन देता है कि / C F dr = 0. तो F के पास G में बंद लूप गुण है और इसलिए वहां एक ढाल क्षेत्र है।ग्रीन्स प्रमेय का एक इंजीनियरिंग अनुप्रयोग प्लमीमीटर है, जो मापने योग्य क्षेत्रों के लिए एक यांत्रिक उपकरण है।
उपर्युक्त सवालों के जवाब द्वारा ग्रीन प्रमेय का प्रमाण (Green Theorem Proof,Proof of Green Theorem) को ओर अधिक स्पष्ट रूप से समझा जा सकता है।
Also Read This Article:-Derivative of vectors
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |